Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Giải nhanh nguyên hàm tích phân và ứng dụng bằng máy tính Casio - Hoàng Văn Bình, tài liệu bao gồm 44 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Giải nhanh nguyên hàm tích phân và ứng dụng bằng máy tính Casio - Hoàng Văn Bình
Nguyên hàm - tích phân
Bài 1. Nguyên hàm
I. Lý thuyết
1. Nguyên hàm \(\int f (x)dx = F(x) + C\)
2. Tính chất
\( - {\left( {\int f (x)dx} \right)^\prime } = f(x){\rm{ v\`a }}\int f (x)dx = f(x) + C\)
\( - \int k \cdot f(x)dx = k\int f (x)dx(k \ne 0)\)
\[\smallint [f(x) \pm g(x)]dx = \smallint f(x)dx \pm \smallint g(x)dx\]
3. Bảng nguyên hàm
|
\[\smallint kdx = kx + C\quad (k = const)\] |
|
|
\(\int {\frac{1}{x}} dx = \ln |x| + C\) |
\(\int {{u^\alpha }} dx = \frac{{{u^{\alpha + 1}}}}{{\alpha + 1}} + C\) |
|
\(\int {{e^x}} dx = {e^x} + C\) |
\(\int {\frac{1}{u}} dx = \ln |u| + C\) |
|
\(\int {{x^\alpha }} dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\quad (\alpha \ne - 1)\) |
\(\int {{e^u}} dx = {e^u} + C\) |
|
\(\int {{a^x}} dx = \frac{{{a^x}}}{{\ln a}} + C\) |
\(\int {{a^u}} dx = \frac{{{a^u}}}{{\ln a}} + C\) |
|
\(\int {\cos } xdx = \sin x + C\) |
\(\int {\cos } udx = \sin u + C\) |
|
\(\int {\sin } xdx = - \cos x + C\) |
\(\int {\sin } udx = - \cos u + C\) |
|
\(\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C\) |
\(\int {\frac{1}{{{{\cos }^2}u}}} dx = \tan u + C\) |
|
\(\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\) |
\(\int {\frac{1}{{{{\sin }^2}u}}} dx = - \cot u + C\) |
|
\(\int {\sqrt {{a^2} - {x^2}} } dx = \frac{{{a^2}}}{2}\arcsin \frac{x}{a} + \frac{{x\sqrt {{a^2} - {x^2}} }}{2} + C\) |
\(\int {\frac{1}{{\sqrt {{a^2} - {x^2}} }}} = \arcsin \frac{x}{a} + C\) |
|
\(\int {\frac{{dx}}{{{a^2} - {x^2}}}} = \frac{1}{{2a}}\ln \left| {\frac{{a + x}}{{a - x}}} \right| + C\) |
\(\int {\frac{{dx}}{{{a^2} + {x^2}}}} = \frac{1}{a}\arctan \frac{x}{a} + C\) |
|
\(\int {\sqrt {{x^2} \pm {a^2}} } dx = \frac{x}{2}\sqrt {{x^2} \pm {a^2}} + \frac{a}{2}\ln \left| {x + \sqrt {{x^2} \pm {a^2}} } \right| + C\) |
\(\int {\frac{{dx}}{{\sqrt {{x^2} + k} }}} = \ln \left| {x + \sqrt {{x^2} + k} } \right| + C\) |
4. Các phương pháp tìm nguyên hàm
a. Phương pháp đổi biến số
Nếu \(\int f (x)dx = F(x) + C\) thì \(\int f \left[ {u(x) \cdot {u^\prime }(x)} \right]dx = F(u(x)) + C\)
Đặt \(t = u(x) \Rightarrow dt = {u^\prime }(x)dx\). Khi đó \(\int f (t)dt = F(t) + C = F[u(x)] + C\)
Cách đặt biến:
Dạng 1: Đặt biến thường
\( + \int f (ax + b)dx\) đặt \(t = ax + 10.\)
\( + \int {\frac{{f(\sqrt x )}}{{\sqrt x }}} dx\) đặt \(t = \sqrt x \)
\( + \int f (\tan x)dx\) đặt \(t = \tan x\)
\( + \int f \left( {{x^{n + 1}}} \right) \cdot xdx\) đặt \(t = {x^{n + 1}}\)
\( + \int f (\cot x)dx\) đặt \(t = \cot x\)
\( + \int f (\sin x)\cos xdx\) đặt \(t = \sin x\)
\( + \int {\frac{{f(\ln x)}}{x}} dx\) đặt \(t = \ln x\)
\( + \int f \left( {{e^x}} \right){e^x}dx\) đặt \(t = {e^x}\)
\( + \int f (\cos x)\sin xdx\) đặt \(t = \cos x\)
Dạng 2: Đặt lượng giác:
\( + \left\{ {\begin{array}{*{20}{l}}{\sqrt {{a^2} + {x^2}} }\\{\frac{1}{{\sqrt {{a^2} + {x^2}} }}}\\{\frac{1}{{{a^2} + {x^2}}}}\end{array}\left\{ {\begin{array}{*{20}{l}}{x = a\tan t}\\{x = a\cot t}\end{array}} \right.} \right.\)
\( + \left\{ {\begin{array}{*{20}{l}}{\sqrt {{a^2} - {x^2}} }\\{\frac{1}{{\sqrt {{a^2} - {x^2}} }}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = a\sin t}\\{x = a\cos t}\end{array}} \right.} \right.\)
\( + \left\{ {\begin{array}{*{20}{l}}{\sqrt {{x^2} - {a^2}} }\\{\frac{1}{{\sqrt {{x^2} - {a^2}} }}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{a}{{\sin t}}}\\{x = \frac{a}{{\cos t}}}\end{array}} \right.} \right.\)
Sau khi tìm được nguyên hàm theo t thì ta thay ngược lại vào f(x).
b. Phương pháp nguyên hàm từng phần
Cho hai hàm số u = u(x) và v = v(x) liên tục và có đạo hàm trên đoạn [a ; b] thì khi đó ta có \(\int u dv = uv - \int v du\)
Cách làm: đặt theo quy tắc: "nhất loga - nhì đa - thức tam - lượng tứ mũ"
c. Dạng nguyên hàm hữu tỉ
- Nguyên hàm dạng: \(\int {\frac{{{\rm{d}}x}}{{ax + b}}} = \frac{1}{a}\ln |ax + b| + C\)
- Nguyên hàm dạng:
\(\int {\frac{{{\rm{d}}x}}{{a{x^2} + bx + c}}} = \frac{1}{{a\left( {{x_1} - {x_2}} \right)}}\ln \left| {\frac{{x - {x_1}}}{{x - {x_2}}}} \right| + C\) với \(\Delta > 0\)
- Nguyên hàm dạng: \(\int {\frac{{P(x)}}{{G(x)}}} {\rm{d}}x\)
- Nếu Q(x) là tích các nghiệm đơn
\(Q(x) = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_n}} \right)\) thì ta tách
\(\int {\frac{{P(x)}}{{G(x)}}} {\rm{d}}x = \int {\left( {\frac{{{A_1}}}{{x - {x_1}}} + \frac{{{A_2}}}{{x - {x_2}}} + \ldots + \frac{{{A_n}}}{{x - {x_n}}}} \right)} {\rm{d}}x\)
- Nếu Q(x) là tích các nghiệm đơn và nghiệm bội giả sử như \(Q(x) = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right){\left( {x - {x_3}} \right)^n}\) thì ta tách
\(\int {\frac{{P(x)}}{{G(x)}}} {\rm{d}}x = \int {\left( {\frac{{{A_1}}}{{x - {x_1}}} + \frac{{{A_2}}}{{x - {x_2}}} + \frac{{{B_1}}}{{x - {x_3}}} + \frac{{{B_2}}}{{{{\left( {x - {x_3}} \right)}^2}}} + \ldots + \frac{{{B_{n - 1}}}}{{{{\left( {x - {x_3}} \right)}^{n - 1}}}} + \frac{{{B_n}}}{{{{\left( {x - {x_3}} \right)}^n}}}} \right)} {\rm{d}}x\)
- Nếu Q(x) là tích các nghiệm đơn và một tam thức bậc hai vô nghiệm giả sử
\(\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {{x^2} + px + q} \right),\Delta = {p^2} - 4q < 0{\rm{ }}\)
Thì ra tách\({\rm{ }}\int {\frac{{P(x)}}{{G(x)}}} {\rm{d}}x = \int {\left( {\frac{{{A_1}}}{{x - {x_1}}} + \frac{{{A_2}}}{{x - {x_2}}} + \frac{{Bx + C}}{{{x^2} + px + q}}} \right)} {\rm{d}}x\)
d. Dạng nguyên hàm vô tỉ
- Nguyên hàm dạng \(R\left( {x,\sqrt {{a^2} - {x^2}} } \right)\) đặt \(\left\{ {\begin{array}{*{20}{l}}{x = a\sin t}\\{x = a\cos t}\end{array}} \right.\)
- Nguyên hàm dạng \(R\left( {x,\sqrt {{a^2} + {x^2}} } \right)\) đặt \(x = a\) tant
- Nguyên hàm dạng \(R\left( {x,\sqrt {{x^2} - {a^2}} } \right)\) đặt \(x = \frac{a}{{\cos t}}\)
- Nguyên hàm dạng \(R\left( {x,\sqrt {\frac{{a - x}}{{a + x}}} } \right)\) đặt \(x = a\cos 2t\)
- Nguyên hàm dạng \(R\left( {x,\sqrt[n]{{\frac{{ax + b}}{{cx + d}}}}} \right)\) đặt \(t = \sqrt[n]{{\frac{{ax + b}}{{cx + d}}}}\)
- Nguyên hàm dạng \(R = \frac{1}{{{{(ax + b)}^n}\sqrt {\alpha {x^2} + \beta x + \gamma } }}\) đặt \(t = \frac{1}{{ax + b}}\)
e. Dạng nguyên hàm lượng giác
- Nguyên hàm dạng \(\int {{{\sin }^n}} x \cdot \cos {x^m}\;{\rm{d}}x\quad (m,n \in \mathbb{N})\)
- m, n chẵn thì dùng công thức hạ bậc,
- m lẻ thì đặt u = sin x, n lẻ thì đặt u = cos x
f. Một số dạng tích phân đặc biệt
- Cho hàm số f(x) liên tục là hàm lẻ trên [-a ; a] thì ta có \(\int_{ - a}^a f (x)dx = 0\).
- Cho hàm số f(x) liên tục là hàm chăn trên \([ - \alpha ;\alpha ]\) thì ta có \(\int_{ - \alpha }^\alpha {\frac{{f(x)}}{{{a^x} + 1}}} dx = \int_0^a f (x)dx\).
- Cho hàm số f(x) liên tục trên \(\left[ {0;\frac{\pi }{2}} \right]\) thì ta có \(\int_0^{\frac{\pi }{2}} f (\sin x)dx = \int_0^{\frac{\pi }{2}} f (\cos x)dx\).
II. Sử dụng máy tính cầm tay
Bấm máy tính như sau: \({\left. {\frac{d}{{dx}}(DA)} \right|_{x = X}} - DB\)
1. Tích phân hữu tỉ
\( \oplus \) Dạng \(\int {\frac{{P(x)}}{{Q(x)}}} \) trong đó bậc của \(P(x) \ge Q(x)\). Ta thực hiện phép chia đa thức. Áp dụng phương pháp CALC 100
Ta giả sử \(Q(x) = \left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\) (nhiều hay ít hơn cũng làm tương tự):
\(\frac{{P(x)}}{{Q(x)}} = \frac{A}{{x - {x_1}}} + \frac{B}{{x - {x_2}}} + \frac{C}{{x - {x_3}}} + R(x)\) trong đó R(x) là biểu thức dư của phép chia.
\({\rm{ T\`i m }}\left\{ {\begin{array}{*{20}{l}}{A = \frac{d}{{dx}}\left( {\frac{{P(x)}}{{\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)}}} \right)\mid x = {x_1}}\\{B = {{\left. {\frac{d}{{dx}}\left( {\frac{{P(x)}}{{\left( {x - {x_1}} \right)\left( {x - {x_3}} \right)}}} \right)} \right|}_{x = {x_2}}}.}\\{C = {{\left. {\frac{d}{{dx}}\left( {\frac{{P(x)}}{{\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)}}} \right)} \right|}_{x = {x_3}}}}\end{array}} \right.\)
Tìm \(R(x) = {\left. {\frac{d}{{dx}}\left( {\frac{{P(x)}}{{\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)}} - \frac{A}{{x - {x_1}}} - \frac{B}{{x - {x_2}}} - \frac{C}{{x - {x_3}}}} \right)} \right|_{x = 100}}\) sử dụng cách tách 100
\( \oplus \) Dạng \(f(x) = \frac{{ax + b}}{{\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)}}\) cần tách đưa về dạng \(\frac{A}{{x - {x_1}}} + \frac{B}{{x - {x_2}}}\)
Cách 1. Bấm: \(\frac{{aX + b}}{{{{\left. {\frac{d}{{dx}}\left[ {\left( {X - {x_1}} \right)\left( {X - {x_2}} \right)} \right]} \right|}_{x = X}}}}\)
CALC \(X = {x_1} \to A\)
CALC \(X = {x_2} \to B\)
Cách 2. Bấm: \(\frac{{aX + b}}{{\left( {X - {x_1}} \right)\left( {X - {x_2}} \right)}} \cdot \left( {X - {x_1}} \right)\)
CALC \(X = {x_1} + 0,0000001 \to A\)
CALC \(X = {x_2} + 0,0000001 \to B\)
Cách 3: Bấm \(\left\{ {\begin{array}{*{20}{l}}{A = {{\left. {\frac{d}{{dx}}\left( {\frac{{ax + b}}{{x - {x_2}}}} \right)} \right|}_{x = {x_1}}}}\\{B = {{\left. {\frac{d}{{dx}}\left( {\frac{{ax + b}}{{x - {x_1}}}} \right)} \right|}_{x = {x_2}}}}\end{array}} \right.\)
Cả ba cách trên nếu tìm nguyên hàm đều cho dạng: \(A\ln \left| {x - {x_1}} \right| + B\ln \left| {x - {x_2}} \right| + C\).
VD. Tách \(F(x) = \frac{{{x^2} + 2x + 6}}{{{x^3} - 7{x^2} + 14x - 8}}\) thành các phân thức tối giản
\(F(x) = \frac{{{x^2} + 2x + 6}}{{{x^3} - 7{x^2} + 14x - 8}} = \frac{{{x^2} + 2x + 6}}{{(x - 1)(x - 2)(x - 4)}} = \frac{A}{{x - 1}} + \frac{B}{{x - 2}} + \frac{C}{{x - 3}}\)
Bấm: \(\frac{{{X^2} + 2X + 6}}{{{{\left. {\frac{d}{{dx}}[(X - 1)(X - 2)(X - 4)]} \right|}_{x = X}}}}\)
CALC X = 1 hệ số A = 3
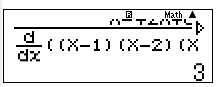
CALC X = 2 hệ số B = -7
CALC X = 4 hệ số C = 5
Vậy \(F(x) = \frac{{{x^2} + 2x + 6}}{{{x^3} - 7{x^2} + 14x - 8}} = \frac{3}{{x - 1}} - \frac{7}{{x - 2}} + \frac{5}{{x - 3}}\)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
