Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 68 Bài tập vận dụng nguyên hàm tích phân và ứng dụng, tài liệu bao gồm 49 trang, 68 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu gồm những nội dung sau:

Phần 1: Nguyên hàm

Phần 2: Tích phân

Phần 3: Ứng dụng tích phân, nguyên hàm giải toán

68 Bài tập vận dụng nguyên hàm tích phân và ứng dụng - có đáp án và lời giải

Chương 3. Nguyên hàm - tích phân & ứng dụng tích phân

Phần 1. Nguyên hàm

Câu 1. (Chuyên Lam Sơn - 2020) Cho \(f(x)\) và \(g(x)\) là hai hàm số liên tục và có một nguyên hàm lần lượt là \(F(x) = x + 2019,G(x) = {x^2} + 2020\). Tìm một nguyên hàm \(H(x)\) của hàm số \(h(x) = f(x) \cdot g(x)\), biết \(H(1) = 3\).

A. \[H(x) = {x^3} + 3\]

B. \[H(x) = {x^3} + 5\]

C. \[H(x) = {x^3} + 1\]

D. \[H(x) = {x^2} + 2\]

Câu 2. (Chuyên Thái Bình – 2020) Gỉa sử \[F(x) = \left( {a{x^2} + bx + c} \right){e^x}\] là 1 nguyên hàm của hàm số \[f(x) = {x^2}{e^x}\]. Tính tích P = abc.

A. P = - 4

B. P = 1

C. P = 5

D. P = - 3

Câu 3. ( Chuyên Phan Bội Châu – Nghệ An – 2020) Cho hàm số y = f(x) đồng biến và có đạo hàm liên tục trên \(\mathbb{R}\) thỏa mãn \({\left( {{f^\prime }(x)} \right)^2} = f(x) \cdot {e^x},\forall x \in \mathbb{R}\) và \(f(0) = 2\). Khi đó \(f(2)\) thuộc khoảng nào sau đây?

A. ( 12; 13)

B. (9; 10).

C. (11; 12)

D. (13; 14)

Câu 4. (Chuyên Thái Bình – 2020) Cho hàm số f = f(x) thỏa mãn \[f(2) =  - \frac{4}{{19}}\] và \[f'(x) = {x^3}{f^2}(x)\forall x \in \mathbb{R}\]. Gía trị của f(1) bằng

A. \[ - \frac{2}{3}\]

B. \[ - \frac{1}{2}\]

C. -1

D. \[ - \frac{3}{4}\]

Câu 5. ( Bỉm Sơn – Thanh Hoá – 2020) Cho hàm số  và F(x) là 1 nguyên hàm của \[x \cdot f'(x)\] thỏa mã F(0) = 0. Biết \[a \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\]thỏa mãn \(\tan a = 3\). Tính giá trị biểu thức \(T = F(a) - 10{a^2} + 3a\).

A. \( - \frac{1}{2}\ln 10\).

B. \(\frac{1}{2}\ln 10\).

C. \( - \frac{1}{4}\ln 10\).

D. \(\ln 10\).

Câu 6. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\backslash \{  - 1;0\} \) thỏa mãn điều kiện: \(f(1) =  - 2\ln 2\) và \(x.(x + 1) \cdot {f^\prime }(x) + f(x) = {x^2} + x\). Biết \(f(2) = a + b \cdot \ln 3(a,b \in \mathbb{Q})\). Giá trị \(2\left( {{a^2} + {b^2}} \right)\) là

A. \(\frac{{27}}{4}\).

B. 9 .

C. \(\frac{3}{4}\).

D. \(\frac{9}{2}\).

Câu 7. (Yên Lạc 2 - Vĩnh Phúc - 2020) Gọi \(F(x)\) là một nguyên hàm của hàm số \(f(x) = {2^x}\), thỏa mãn \(F(0) = \frac{1}{{\ln 2}}\). Tính giá trị biểu thức \(T = F(0) + F(1) + F(2) +  \ldots  + F(2019)\).

A. \(T = \frac{{{2^{2020}} - 1}}{{\ln 2}}\).

B. \(T = 1009.\frac{{{2^{2019}} - 1}}{2}.\quad \)

C. \(T = {2^{2019.2020}}\).

D. \(T = \frac{{{2^{2019}} - 1}}{{\ln 2}}\).

Câu 8. (Hải Hậu - Nam Định - 2020) Cho hàm số \(y = f(x)\) thỏa mãn \(f(x) < 0,\forall x > 0\) và có đạo hàm \({f^\prime }(x)\) liên tục trên khoảng \((0; + \infty )\) thỏa mãn \({f^\prime }(x) = (2x + 1){f^2}(x),\forall x > 0\) và \(f(1) =  - \frac{1}{2}\). Giá trị của biểu thức \(f(1) + f(2) +  \ldots  + f(2020)\) bằng

A. \( - \frac{{2020}}{{2021}}\).

B. \( - \frac{{2015}}{{2019}}\).

C. \( - \frac{{2019}}{{2020}}\).

D. \( - \frac{{2016}}{{2021}}\).

Câu 9. (Trường VINSCHOOL - 2020) Cho hàm số \(f(x)\) xác định trên \(R\backslash \{  - 1;1\} \) thỏa mãn \({f^\prime }(x) = \frac{1}{{{x^2} - 1}}\). Biết \(f(3) + f( - 3) = 4\) và \(f\left( {\frac{1}{3}} \right) + f\left( {\frac{{ - 1}}{3}} \right) = 2\). Giá trị của biểu thức \(f( - 5) + f(0) + f(2)\) bằng

A. \(5 - \frac{1}{2}\ln 2\).

B. \(6 - \frac{1}{2}\ln 2\).

C. \(5 + \frac{1}{2}\ln 2\).

D. \(6 + \frac{1}{2}\ln 2\).

Phần 2. Tích phân

Câu 10. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số \(f(x)\) liên tục trên \([ - 1;2]\) và thỏa mãn điều kiện \(f(x) = \sqrt {x + 2}  + xf\left( {3 - {x^2}} \right)\).Tích phân \(I = \int_{ - 1}^2 f (x)dx\) bằng

A. \(I = \frac{{14}}{3}\).

B. \(I = \frac{{28}}{3}\).

C. \(I = \frac{4}{3}\).

D. \(I = 2\).

Câu 11. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(\int_{ - 5}^1 f (x){\rm{d}}x = 9\). Tích phân  bằng

A. 15 .

B. 27 .

C. 75 .

D. 21 .

Câu 12. (Chuyên ĐH Vinh - Nghệ An -2020) Cho \(f(x)\) là hàm số có đạo hàm liên tục trên [0 ; 1] và \(f(1) =  - \frac{1}{{18}},\int_0^1 x .{f^\prime }(x){\rm{d}}x = \frac{1}{{36}}\). Giá trị của \(\int_0^1 f (x){\rm{d}}x\) bằng

A. \( - \frac{1}{{12}}\).

B. \(\frac{1}{{36}}\).

C. \(\frac{1}{{12}}\).

D. \( - \frac{1}{{36}}\).

Câu 13. (Chuyên Hưng Yên - 2020) Cho hàm số \(f(x)\) liên tục trên đoạn $[0 ; 1]$ thỏa mãn \(4x.f\left( {{x^2}} \right) + 3f(1 - x) = \sqrt {1 - {x^2}} \). Tính \(I = \int_0^1 f (x){\rm{d}}x\).

A. \(\frac{\pi }{4}\).

B. \(\frac{\pi }{{16}}\).

C. \(\frac{\pi }{{20}}\).

D. \(\frac{\pi }{6}\).

Câu 14. (Chuyên KHTN - 2020) Cho hàm số \(y = f(x)\) biết \(f(0) = \frac{1}{2}\) và \({f^\prime }(x) = x{e^{{x^2}}}\) với mọi \(x \in \mathbb{R}\). Khi đó \(\int_0^1 x f(x)dx\) bằng

A. \(\frac{{e + 1}}{4}\).

B. \(\frac{{e - 1}}{4}\).

C. \(\frac{{e - 1}}{2}\).

D. \(\frac{{e + 1}}{2}\).

Câu 15. (Chuyên Lam Són - 2020) Cho hàm số \(f(x)\) liên tục trên đoạn [0 ; 10] thỏa mãn \(\int_0^{10} f (x){\rm{d}}x = 7,\int_2^{10} f (x){\rm{d}}x = 1\). Tính \(P = \int_0^1 f (2x){\rm{d}}x.\)

A. \(P = 6\).

B. \(P =  - 6\).

C. \(P = 3\).

D. \(P = 12\).

Câu 16. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hàm số \(f(x)\) có \(f(0) = 4\) và \({f^\prime }(x) = 2{\cos ^2}x + 1,\forall x \in \mathbb{R}\) Khi đó \(\int_0^{\frac{\pi }{4}} f (x)dx\) bằng.

A. \(\frac{{{\pi ^2} + 16\pi  + 16}}{{16}}\)

B. \(\frac{{{\pi ^2} + 4}}{{16}}\)

C. \(\frac{{{\pi ^2} + 14\pi }}{{16}}\).

D. \(\frac{{{\pi ^2} + 16\pi  + 4}}{{16}}\).

Câu 17. (Chuyên Lương Văn Ty - Ninh Bình - 2020) Cho hàm số \(f(x)\) có \(f(0) =  - 1\) và \({f^\prime }(x) = x\left( {6 + 12x + {e^{ - x}}} \right),\forall x \in \mathbb{R}\). Khi đó \(\int_0^1 f (x){\rm{d}}x\) bằng

A. 3e.

B. \(3{e^{ - 1}}\).

C. \(4 - 3{e^{ - 1}}\).

D. \( - 3{e^{ - 1}}\).

Câu 18. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Biết rằng   với a, b, c là các số nguyên dương và \(\frac{b}{c}\) là phân số tối giản. Tính \(S = a + b + c\).

A. S  = 3

B. S  = 7

C. S  = 10

D. S  = 5

Câu 19. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam-2020) Cho hàm số \(f(x)\) liên tục trên khoảng \((0; + \infty )\). Biết \(f(3) = 3\) và \(x{f^\prime }(2x + 1) - f(2x + 1) = {x^3},\forall x \in (0; + \infty )\). Giá trị của \(\int_3^5 f (x)dx\) bằng

A. \(\frac{{914}}{3}\).

B. \(\frac{{59}}{3}\)

C. \(\frac{{45}}{4}\)

D. 88 .

Câu 20. (Chuyên Thái Bình - 2020) Cho hàm số \(f(x)\) có đạo hàm và đồng biến trên [1 ; 4], thỏa mãn \(x + 2xf(x) = {\left[ {{f^\prime }(x)} \right]^2}\) với mọi \(x \in [1;4]\). Biết \(f(1) = \frac{3}{2}\), tính \(I = \int_1^4 f (x)dx\)

A. \(\frac{{1188}}{{45}}\)

B. \(\frac{{1187}}{{45}}\).

C. \(\frac{{1186}}{{45}}\).

D. \(\frac{9}{2}\).

Câu 21. (Chuyên Bắc Ninh - 2020) Cho \(I = \int_1^5 f (x){\rm{d}}x = 26\). Khi đó\(J = \int_0^2 x \left[ {f\left( {{x^2} + 1} \right) + 1} \right]{\rm{d}}x\) bằng

A. 15 .

B. 13 .

C. 54 .

D. 52 .

Câu 22. (Chuyên Bắc Ninh - 2020) Biết \(I = \int_0^4 x \ln \left( {{x^2} + 9} \right){\rm{d}}x = a\ln 5 + b\ln 3 + c\) trong đó a, b, c là các số thực. Tính giá trị của biểu thức \(T = a + b + c\).

A. \(T = 9\).

B. \(T = 11\).

C. \(T = 8\).

D. \(T = 10\).

Câu 23. (Chuyên Bắc Ninh - 2020) Cho hàm số \(f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(\int_0^1 f (x){\rm{d}}x = 10,f(1) = \cot 1\). Tính tích phân \(I = \int_0^1 {\left[ {f(x){{\tan }^2}x + {f^\prime }(x)\tan x} \right]} {\rm{d}}x\).

A. \(1 - \ln (\cos 1)\).

B. \( - 1\).

C. \( - 9\).

D. \(1 - \cot 1\).

Câu 24. (Chuyên Bến Tre - 2020) Cho hàm số \(y = f(x)\) thỏa mãn \({\left[ {{f^\prime }(x)} \right]^2} + f(x) \cdot {f^{\prime \prime }}(x) = {x^3} - 2x,\forall x \in R\) và \(f(0) = {f^\prime }(0) = 2\). Tính giá trị của \(T = {f^2}(2)\)

A. \(\frac{{160}}{{15}}\)

B. \(\frac{{268}}{{15}}\)

C. \(\frac{4}{{15}}\)

D. \(\frac{{268}}{{30}}\)

Câu 25. (Chuyên Chu Văn An - 2020) Cho hàm số \(y = f(x)\) liên tục, có đạo hàm trên \(R\) thỏa mãn điều kiện \[f(x) + x\left( {f'(x) - 2\sin x} \right) = {x^2}\cos x,x \in R{\rm{\;v\`a \;}}f\left( {\frac{\pi }{2}} \right) = \frac{\pi }{2}\]. Tính .

A. 0 .

B. \(\frac{\pi }{2}\).

C. 1 .

D. \(\pi \).

Câu 26. (Chuyên Chu Văn An - 2020) Hàm số \(y = f(x)\) có đồ thị như hình vẽ sau:

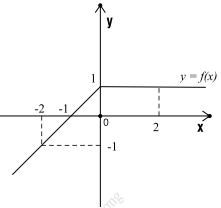
Giá trị của \(\int_{ - 2}^2 f (x)dx\) bằng

A. 3 .

B. 1 .

C. 0

D. 2

Câu 27. ( Chuyên Hùng Vương – Gia Lai – 2020) Cho hàm số f(x) liên tục và là hàm số lẻ trên đoạn \([ - 2;2]\). Biết rằng \(\int_{ - 1}^0 f (x)\) A. \(\int_{ - 2}^2 f (x)dx = 2\int_0^2 f (x)dx.\) Mệnh đề nào sau đây đúng?

A. \(\int_{ - 2}^2 f (x)dx = 2\int_0^2 f (x)dx\)

B.

C. \(\int_0^1 f (x)dx =  - 1\).

D. \(\int_0^2 f (x)dx =  - 3\).

Câu 28. (Chuyên Hùng Vương – Phú Thọ - 2020) Xét hàm số. Gía trị của f (ln(5620)) bằng

A. 5622 .

B. 5620 .

C. 5618 .

D. 5621 .

Câu 29. ( Chuyên Lào Cai – 2020) Cho hàm số y = f(x) liên tục tục trên \(\mathbb{R}\) thỏa

mãn \(\int_1^9 {\frac{{f(\sqrt x )}}{{\sqrt x }}} dx = 4\) và . Tích phân  bằng

A. I = 8

B. I = 6

C. I = 4

D. I = 10

Câu 30. (Chuyên Lào Cai - 2020) Cho hàm số \(f(x)\) có đạo hàm liên tục trên [0 ; 3] thỏa mãn \(f(3) = 0,\int_0^3 {{{\left[ {{f^\prime }(x)} \right]}^2}} dx = \frac{7}{6}\) và \(\int_0^3 {\frac{{f(x)}}{{\sqrt {x + 1} }}} dx =  - \frac{7}{3}\). Tích phân \(\int_0^3 f (x)dx\) bằng:

A. \( - \frac{7}{3}\).

B. \(\frac{{ - 97}}{{30}}\).

C. \(\frac{7}{6}\).

D. \(\frac{{ - 7}}{6}\).

Câu 31. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số \(f(x)\) thỏa mãn \(f(0) = \frac{2}{3}\) và \((\sqrt x  + \sqrt {x + 1} ){f^\prime }(x) = 1,\forall x \ge  - 1\). Biết rằng \(\int_0^1 f (x)dx = \frac{{a\sqrt 2  + b}}{{15}}\) với \(a,b \in \mathbb{Z}\). Tính \(T = a + b\).

A. \( - 8\).

B. \( - 24\).

C. 24 .

D. 8 .

Câu 32. (Chuyên Sơn La - 2020) Cho \(f(x)\) là hàm số liên tục trên \(\mathbb{R}\) thỏa \(f(1) = 1\) và \(\int_0^1 f (t){\rm{d}}t = \frac{1}{3}\). Tính \(I = \int_0^{\frac{\pi }{2}} {\sin } 2x \cdot {f^\prime }(\sin x){\rm{d}}x\)

A. \(I = \frac{4}{3}\).

B. \(I = \frac{2}{3}\).

C. \(I =  - \frac{2}{3}\)

D. \(I = \frac{1}{3}\).

Câu 33. (Chuyên Sơn La - 2020) Tích phân \(\int_{ - 2}^2 {\frac{{{x^{2020}}}}{{{e^x} + 1}}}  \cdot {\rm{d}}x = \frac{{{2^a}}}{b}\). Tính tổng \(S = a + b\).

A. \(S = 0\).

B. \(S = 2021\).

C. \(S = 2020\).

D. \(S = 4042\).

Câu 34. (Chuyên Thái Bình - 2020) Cho \(f(x)\) là hàm số liên tục trên tập xác đinh \({\mathbb{R}^ + }\)và thỏa mãn \(f\left( {{x^2} + 3x + 1} \right) = x + 2\). Tính \(I = \int_1^5 f (x){\rm{d}}x\)

A. \(\frac{{37}}{6}\).

B. \(\frac{{527}}{3}\).

C. \(\frac{{61}}{6}\).

D. \(\frac{{464}}{3}\).

Câu 35. (Chuyên Vĩnh Phúc - 2020) Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và \(\int_1^9 {\frac{{f(\sqrt x )}}{{\sqrt x }}} \;{\rm{d}}x = 4,\int_0^{\frac{\pi }{2}} f (\sin x)\cos x\;{\rm{d}}x = 2\). Tính tích phân \(I = \int_0^3 f (x){\rm{d}}x.\)

A. I = 6

B. I = 4

C. I = 10

D. I = 2

Câu 36. ( Đại Học Hà Tĩnh – 2020) Cho hàm số f(x) liên tục trên đoạn [ - ln2; ln2] và thảo mãn \[f(x) + f( - x) = \frac{1}{{{{\rm{e}}^x} + 1}}\]. Biết . Tính p = a + b.

A. P = - 2

B. \[P = \frac{1}{2}\]

C. P = - 1

D. P =  2

Câu 37. Cho hàm số f(x) liên tục trên đoạn [0;1] thỏa mãn điều kiện }\end{array}$ \(\int_0^1 f (x)dx = 2\) và \(\int_0^1 x f(x)dx = \frac{3}{2}\). Hỏi giá trị nhỏ nhất của \(\int_0^1 {{f^2}} (x)dx\) bằng bao nhiêu?

A. \(\frac{{27}}{4}\).

B. \(\frac{{34}}{5}\).

C. 7 .

D. 8 .