Bài toán 2. Lập phương trình mặt cầu trong các trường hợp sau:

a) Đi qua điểm \[A(2; - 1; - 3)\] và có tâm \[I(3; - 2;1)\].

b) Nhận đoạn AB làm đường kính với \[A(6;2; - 5),B( - 4;0;7)\].

Giải

a) Phương trình mặt cầu tâm \[I(a;b;c)\], bán kính R:

    \[{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\]

Mặt cầu có tâm \[I(3; - 2;1)\] và đi qua điểm \[A(2; - 1; - 3)\]

nên bán kính \[R = IA = 3\sqrt 2 \], do đó phương trình mặt cầu:

    \[{(x - 3)^2} + {(y + 2)^2} + {(z - 1)^2} = 18\].

b) Mặt cầu nhận AB làm đường kính nên tâm I là trung điểm của AB, do đó \[I(1;1;1)\] và có bán kính

    \[R = \frac{{AB}}{2} = \frac{1}{2}\sqrt {100 + 4 + 144}  = \sqrt {62} \]

Phương trình mặt cầu: \[{(x - 1)^2} + {(y - 1)^2} + {(z - 1)^2} = 62\].

hay: \[{x^2} + {y^2} + {z^2} - 2x - 2y - 2z - 59 = 0\]

Bài toán 3. Lập phương trình mặt cầu:

a) Đi qua ba điểm \[A(0;8;0),B(4;6;2),C(0;12;4)\] và có tâm nằm trên \[mp(Oyz)\].

b) Có đường tròn lớn là đường tròn ngoại tiếp tam giác ABC với \[A(0; - 2;1),B( - 1;0;1),C(0;0; - 1)\].

Giải

a) Tâm I của mặt cầu nằm trên \[mp(Oyz)\] nên \[I(0;b;c)\].

Ta có \[IA = IB = IC\] nên \[\left\{ \begin{array}{l}I{A^2} = I{B^2}\\I{A^2} = I{C^2}\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}{(8 - b)^2} + {c^2} = {4^2} + {(6 - b)^2} + {(2 - c)^2}\\{(8 - b)^2} + {c^2} = {(12 - b)^2} + {(4 - c)^2}\end{array} \right.\]

Giải ra đựơc \[b = 7\] và \[c = 5\].

Do đó \[I(0;7;5)\], \[R = IA = \sqrt {0 + 1 + 25}  = \sqrt {26} \].

Phương trình mặt cầu tâm \[I(a;b;c)\], bán kính R:

          \[{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\]

Vậy mặt cầu có phương trình: \[{x^2} + {(y - 7)^2} + {(z - 5)^2} = 26\].

b) Gọi \[I(x;y;z)\] là tâm đường tròn ngoại tiếp tam giác ABC.

Ta có:

 \[\begin{array}{l}\overrightarrow {AB}  = ( - 1;2;0),\\\overrightarrow {AC}  = (0;2; - 2),\\\overrightarrow {AI}  = (x;y + 2;z - 1)\end{array}\]

\[ \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = ( - 4;2; - 2)\]

Nên \[I \in (ABC)\]

\[\begin{array}{l} \Leftrightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\overrightarrow {AI}  = 0\\ \Leftrightarrow 2x - y + z - 3 = 0\end{array}\]

Ta có \[\left\{ \begin{array}{l}A{I^2} = B{I^2}\\A{I^2} = C{I^2}\\I \in (ABC)\end{array} \right.\]

\[\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 2x + 4y =  - 3\\y - z =  - 1\\ - 2x + y - z =  - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - \frac{1}{4}\\z = \frac{3}{4}\end{array} \right.\end{array}\]

Nên tâm \[I\left( {1; - \frac{1}{4};\frac{3}{4}} \right)\] và bán kính \[R = AI = \sqrt {\frac{{33}}{8}} \]

Vậy PT mặt cầu là \[{(x - 1)^2} + {(y + \frac{1}{4})^2} + {(z - \frac{3}{4})^2} = \frac{{33}}{8}\].

Bài toán 4. Lập phương trình mặt cầu:

a) Có bán kính bằng 2, tiếp xúc với mặt phẳng \[(Oyz)\] và có tâm nằm trên tia Ox.

b) Có tâm \[I(1;2;3)\] và tiếp xúc với \[mp(Oyz)\].

Giải

a) Vì tâm I của mặt cầu nằm trên tia Ox và mặt cầu tiếp xúc với \[mp(Oyz)\] nên điểm tiếp xúc phải là O, do đó bán kính mặt cầu là \[R = IO = 2\] và \[I(2;0;0)\].

Phương trình mặt cầu tâm \[I(a;b;c)\], bán kính R:

           \[{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\]

Vậy mặt cầu có phương trình: \[{(x - 2)^2} + {y^2} + {z^2} = 4\].

b) Vì mặt cầu có tâm \[I(1;2;3)\] và tiếp xúc với \[mp(Oyz)\] nên bán kính R của mặt cầu bằng khoảng cách từ I tới \[mp(Oyz)\].

Do đó \[R = \left| {{x_1}} \right| = 1\].

Mặt cầu có phương trình: \[{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 1\].

Bài toán 5. Cho \[A(1;2; - 4),B(1; - 3;1),C(2;2;3),D(1;0;4)\]. Lập phương trình mặt cầu ngoại tiếp tứ diện ABCD.

Giải

Gọi \[I(a;b;c)\] là tâm mặt cầu ngoại tiếp tứ diện

\[\begin{array}{l}\left\{ \begin{array}{l}IA = IB\\IA = IC\\IA = ID\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}A{I^2} = B{I^2}\\A{I^2} = C{I^2}\\A{I^2} = D{I^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - y + z =  - 1\\x + 7y =  - 2\\ - 2x + 8y =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\y = 1\\z = 0\end{array} \right.\end{array}\]

Do đó \[I( - 2;1;0)\] và \[R = IA = \sqrt {26} \].

Phương trình mặt cầu tâm \[I(a;b;c)\], bán kính R: \[{(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\]

Vậy \[(S):{(x + 2)^2} + {(y - 1)^2} + {z^2} = 26\].

Bài toán 6. Lập phương trình các mặt cầu đối xứng của mặt cầu

\[(S):{x^2} + {y^2} + {z^2} + 4x + 8y - 2z - 4 = 0\].

a) Qua \[mp(xOy)\]

b) Qua \[mp(yOz)\]

Giải

Mặt cầu \[(S):{x^2} + {y^2} + {z^2} + 4x + 8y - 2z - 4 = 0\] có tâm \[I( - 2; - 4;1),R = 5\].

a) Gọi \[(S')\] là mặt cầu đối xứng của \[(S)\] qua \[mp(xOy)\] thì có tâm

    \[I'( - 2; - 4; - 1)\] và \[R' = R = 5\] nên có phương trình:

    \[(S'):{(x + 2)^2} + {(y + 4)^2} + {(z + 1)^2} = 25\].

b) Gọi \[(S'')\] là mặt cầu đối xứng của \[(S)\] qua \[mp(yOz)\] thì

    \[(S'')\] có tâm \[I''(2; - 4;1)\] và \[R'' = R = 5\] nên có phương trình:

    \[(S''):{(x - 2)^2} + {(y + 4)^2} + {(z - 1)^2} = 25\].

Bài toán 7. Cho điểm \[A(3;0;0),B(0;4;0)\]. Lập phương trình mặt cầu có tâm là hình chiếu H của gốc O lên đường thẳng AB và bán kính \[R = \frac{1}{2}\].

Giải

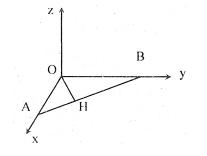
Ta có A thuộc trục Ox, B thuộc trục Oy.

Trong tam giác AOB: \[A{O^2} = AH.AB\]

\[ \Rightarrow AH = \frac{{O{A^2}}}{{AB}} \Rightarrow \frac{{AH}}{{AB}} = \frac{{O{A^2}}}{{A{B^2}}} = \frac{9}{{25}}\]

Do đó \[\overrightarrow {AH}  = \frac{9}{{25}}\overrightarrow {AB}  = \left( { - \frac{{27}}{{25}};\frac{{36}}{{25}};0} \right)\]

\[ \Rightarrow H\left( {\frac{{48}}{{25}};\frac{{36}}{{25}};0} \right)\]

Vậy phương trình mặt cầu cần tìm: \[{\left( {x - \frac{{48}}{{25}}} \right)^2} + {\left( {y - \frac{{36}}{{25}}} \right)^2} + {z^2} = \frac{1}{4}\].

Bài toán 8. Cho điểm \[A(1; - 1;2)\] và \[B(2;0;1)\]

Tìm quỹ tích các điểm M sao cho \[M{A^2} + M{B^2} = 3\].

Giải

Gọi \[M(x;y;z)\].

Ta có: \[M{A^2} + M{B^2} = 3\]

\[ \Leftrightarrow {(1 - x)^2} + {( - 1 - y)^2} + {(2 - z)^2} + {(2 - x)^2} + {y^2} + {(1 - z)^2} = 3\]

\[ \Leftrightarrow {x^2} + {y^2} + {z^2} - 3x + y - 3z + 4 = 0\].

\[ \Leftrightarrow {(x - \frac{3}{2})^2} + {(y + \frac{1}{2})^2} + {(z - \frac{3}{2})^2} = \frac{3}{4}\].

Vậy quỹ tích các điểm M là mặt cầu có tâm \[I(\frac{3}{2}; - \frac{1}{2};\frac{3}{2})\] và bán kính \[R = \frac{{\sqrt 3 }}{2}\].

Bài toán 9. Cho tứ diện với các đỉnh \[A(2;0;0),B(0;4;0),C(0;0;6),D(2;4;6)\]. Tìm tập hợp các điểm M trong không gian sao cho \[\left| {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} } \right| = 4\].

Giải

Gọi \[M(x;y;z)\], suy ra:

\[\begin{array}{l}\overrightarrow {MA}  = ( - x + 2; - y; - 2),\\\overrightarrow {MB}  = ( - x; - y + 4; - z),\end{array}\],

\[\begin{array}{l}\overrightarrow {MC}  = ( - x; - y; - z + 6),\\\overrightarrow {MD}  = ( - x + 2; - y + 4; - z + 6)\end{array}\].

Ta có: \[\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = ( - 4x + 4; - 4y + 8; - 4z + 12)\]

Nên \[\left| {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} } \right| = 4\]

\[ \Leftrightarrow 16.[{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2}] = 16\]

Vậy tập hợp của M là mặt cầu \[{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 1\].