Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 123 bài tập trắc nghiệm quan hệ vuông góc, tài liệu bao gồm 44 trang, 123 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

123 bài tập trắc nghiệm quan hệ vuông góc có lời giải chi tiết

Tuyển chọn 124 bài tập trác nghiệm

Quan hề vuông góc

Có đáp án và lời giải chi tiết

Bài 1: vectơ trong không gian

Câu 1: Cho ba vectơ \(\vec a,\vec b,\vec c\) không đồng phẳng. Xét các vectơ \(\vec x = 2\vec a - \vec b;\vec y =  - 4\vec a + 2\vec b;\vec z =  - 3\vec b - 2\vec c\).

Chọn khẳng định đúng?

A. Hai vectơ \(\vec y;\vec z\) cùng phương.

B. Hai vectơ \(\vec x;\vec y\) cùng phương.

C. Hai vector \(\vec x;\vec z\) cùng phương.

D. Ba vectơ \(\vec x;\vec y;\vec z\) đồng phẳng.

Hướng dẫn giải

+ Nhận thấy: \(\vec y =  - 2\vec x\) nên hai vectơ \(\vec x;\vec y\) cùng phương.

Câu 2: Trong mặt phẳng cho tứ giác ABCD có hai đường chéo cắt nhau tại O. Trong các khẳng định sau, khẳng định nào sai?

A. Nếu ABCD là hình bình hành thì \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \vec 0\).

B. Nếu ABCD là hình thang thì \(\overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  + 2\overrightarrow {OD}  = \vec 0\)

C. Nếu \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \vec 0\) thì $A B C D$ là hình bình hành.

D. Nếu \(\overrightarrow {OA}  + \overrightarrow {OB}  + 2\overrightarrow {OC}  + 2\overrightarrow {OD}  = \vec 0\) thì $A B C D$ là hình thang.

Hướng dẫn giải

Chọn B.

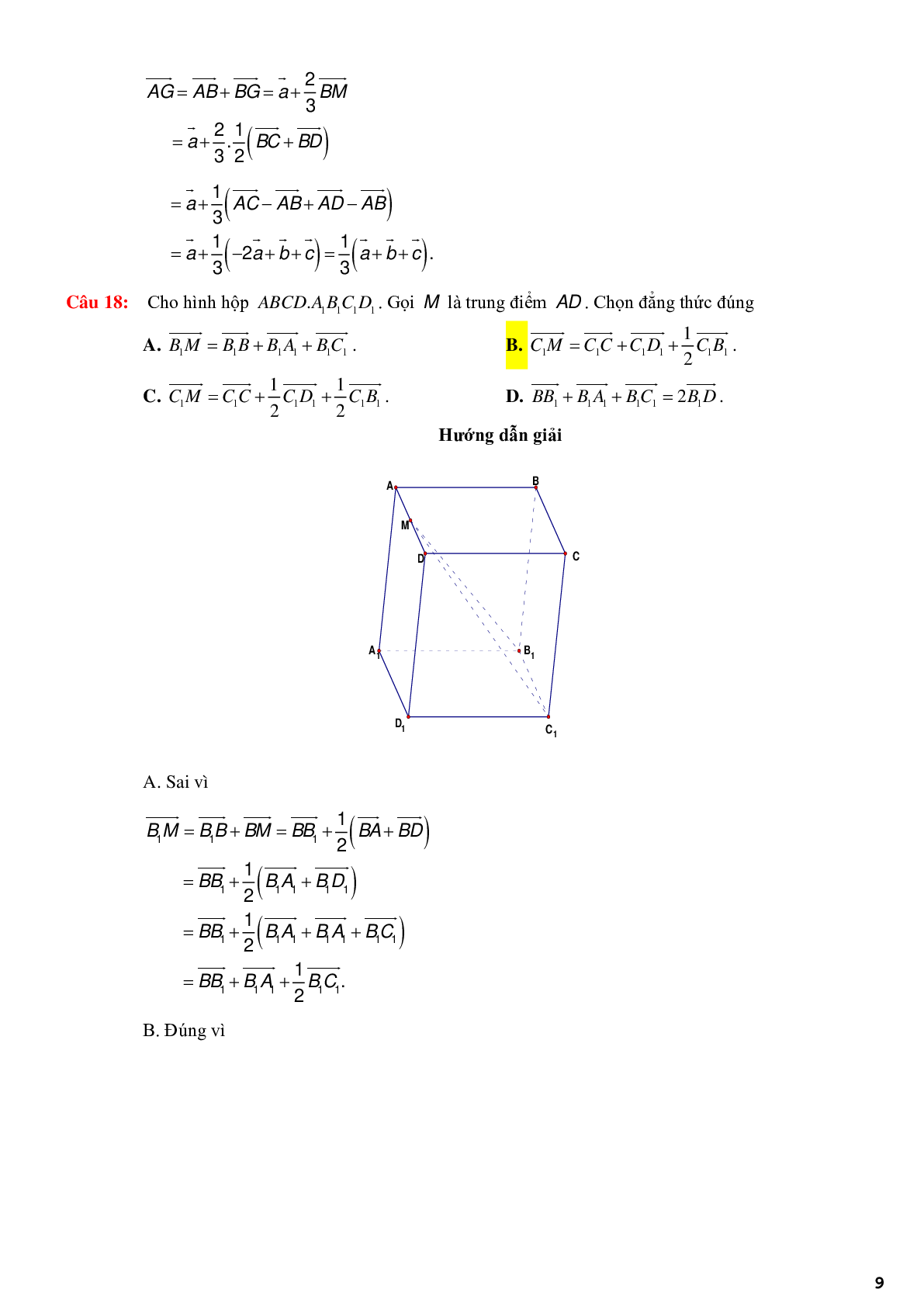
Câu 3: Cho hình hộp \(ABCD \cdot {A_1}{B_1}{C_1}{D_1}\). Chọn khẳng định đúng?

A. \(\overrightarrow {BD} ,\overrightarrow {B{D_1}} ,\overrightarrow {B{C_1}} \) đồng phẳng.

B. \(\overrightarrow {C{D_1}} ,\overrightarrow {AD} ,\overrightarrow {{A_1}{B_1}} \) đồng phẳng.

C. \(\overrightarrow {C{D_1}} ,\overrightarrow {AD} ,\overrightarrow {{A_1}C} \) đồng phẳng.

D. \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {{C_1}A} \) đồng phẳng.

Hướng dẫn giải

+ M,N,P,Q lần lượt là trung điểm của \({\rm{AB}},{\rm{A}}{{\rm{A}}_1},{\rm{D}}{{\rm{D}}_1},CD\).

\(\begin{array}{l} + C{D_1}//(MNPQ).\\ + AD//(MNPQ).\\ + {A_1}C//(MNPQ).\end{array}\)

\( \Rightarrow \overrightarrow {C{D_1}} ,\overrightarrow {AD} ,\overrightarrow {{A_1}C} {\rm{ }}\)đồng phẳng

Câu 4: Cho ba vectơ \(\vec a,\vec b,\vec c\) không đồng phẳng. Xét các vectơ \(\vec x = 2\vec a + \vec b;\vec y = \vec a - \vec b - \vec c;\vec z =  - 3\vec b - 2\vec c\). Chọn khẳng định đúng?

A. Ba vectơ \(\vec x;\vec y;\vec z\) đồng phẳng.

B. Hai vectơ \(\vec x;\vec a\) cùng phương.

C. Hai vectơ \(\vec x;\vec b\) cùng phương.

D. Ba vectơ \(\vec x;\vec y;\vec z\) đôi một cùng phương.

Hướng dẫn giải

Ta có: \(\vec y = \frac{1}{2}(\vec x + \vec z)\) nên ba vectơ \(\vec x;\vec y;\vec z\) đồng phẳng.

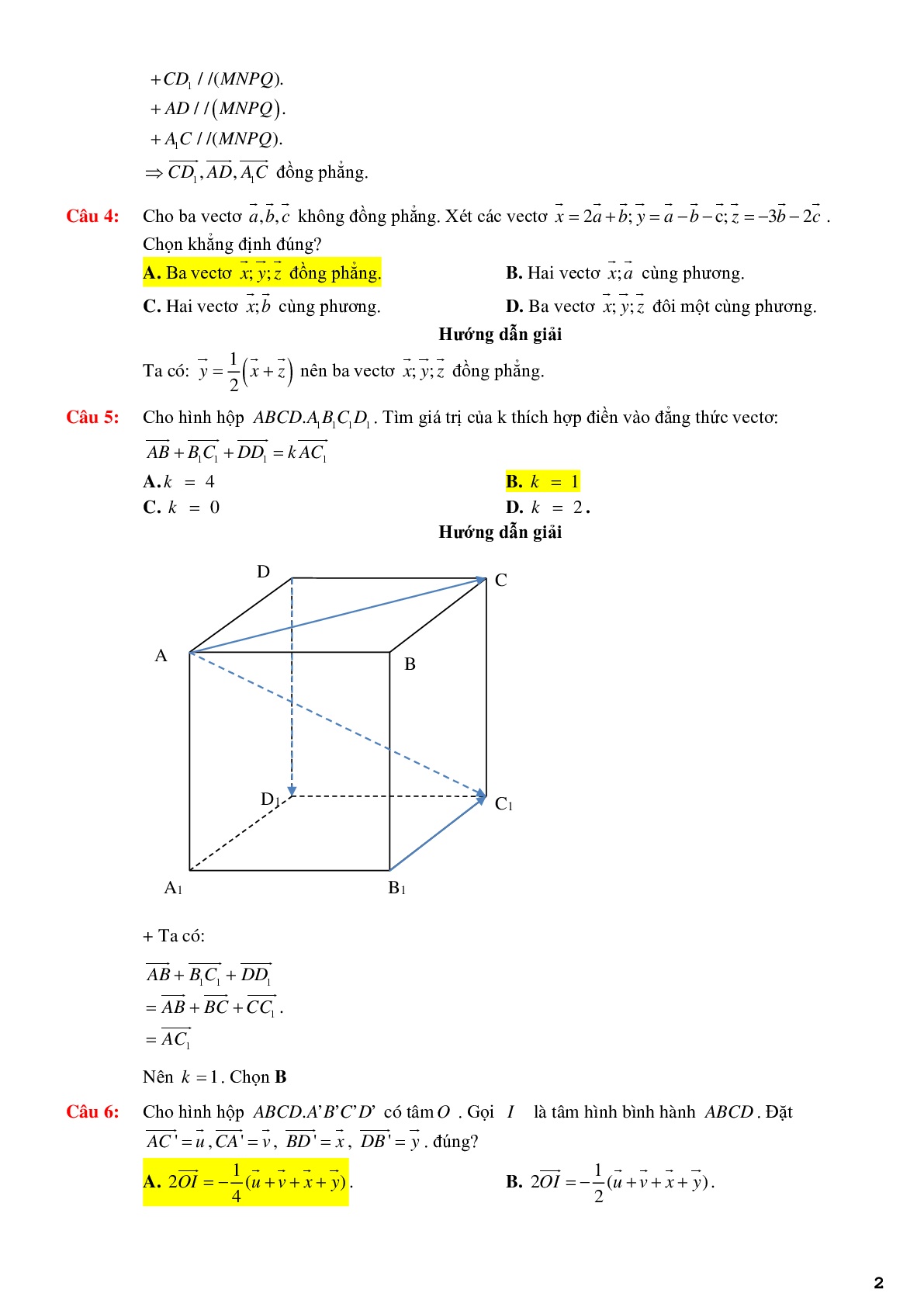
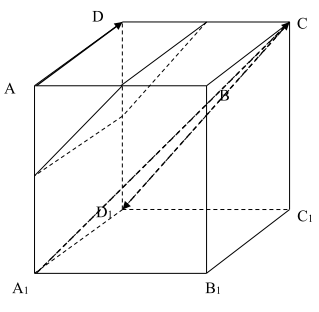
Câu 5: Cho hình hộp \(ABCD \cdot {A_1}{B_1}{C_1}{D_1}\). Tìm giá trị của k thích hợp điền vào đẳng thức vectơ:\(\overrightarrow {AB}  + \overrightarrow {{B_1}{C_1}}  + \overrightarrow {D{D_1}}  = k\overrightarrow {A{C_1}} \)

A. \(k = 4\)

B. \(k = 1\)

C. \(k = 0\)

D. \(k = 2\).

Hướng dẫn giải

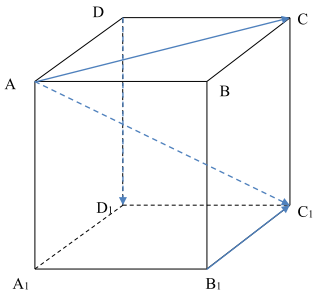
+ Ta có:

\(\begin{array}{l}\overrightarrow {AB}  + \overrightarrow {{B_1}{C_1}}  + \overrightarrow {D{D_1}} \\ = \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {C{C_1}} .\\ = \overrightarrow {A{C_1}} \end{array}\)

Nên k =1. Chọn B

Câu 6: Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt \(\overrightarrow {A{C^\prime }}  = \vec u,\overrightarrow {C{A^\prime }}  = \vec v,\overrightarrow {B{D^\prime }}  = \vec x,\overrightarrow {D{B^\prime }}  = \vec y\). đúng?

A. \(2\overrightarrow {OI}  =  - \frac{1}{4}(\vec u + \vec v + \vec x + \vec y)\).

B. \(2\overrightarrow {OI}  =  - \frac{1}{2}(\vec u + \vec v + \vec x + \vec y)\).

C. \(2\overrightarrow {OI}  = \frac{1}{2}(\vec u + \vec v + \vec x + \vec y)\).

D. \(2\overrightarrow {OI}  = \frac{1}{4}(\vec u + \vec v + \vec x + \vec y)\).

Hướng dẫn giải

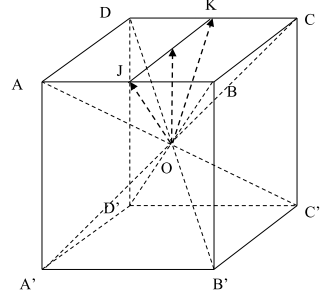
+ Gọi J, K lần lượt là trung điểm AB,CD

\(\begin{array}{l}{\rm{Ta c\'o : }}2\overrightarrow {OI}  = \overrightarrow {{\rm{OJ}}}  + \overrightarrow {OK} \\ = \frac{1}{2}(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD} )\\ =  - \frac{1}{4}(\vec u + \vec v + \vec x + \vec y)\end{array}\)

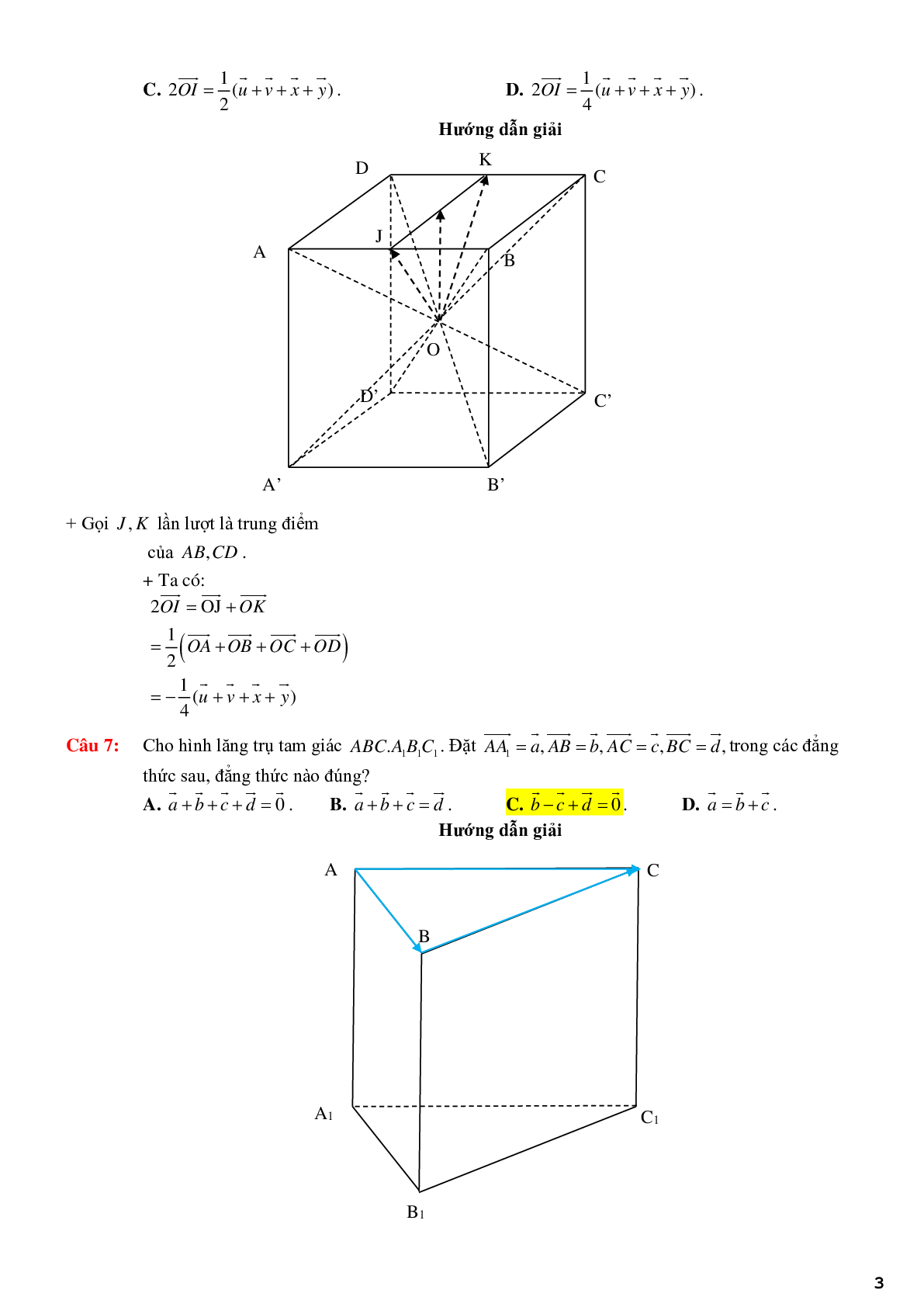
Câu 7: Cho hình lăng trụ tam giác \(ABC \cdot {A_1}{B_1}{C_1}\). Đặt \(\overrightarrow {A{A_1}}  = \vec a,\overrightarrow {AB}  = \vec b,\overrightarrow {AC}  = \vec c,\overrightarrow {BC}  = \vec d\), trong các đẳng thức sau, đẳng thức nào đúng?

A. \(\vec a + \vec b + \vec c + \vec d = \vec 0\).

B. \(\vec a + \vec b + \vec c = \vec d\).

C. \(\vec b - \vec c + \vec d = \vec 0\).

D. \(\vec a = \vec b + \vec c\).

Hướng dẫn giải

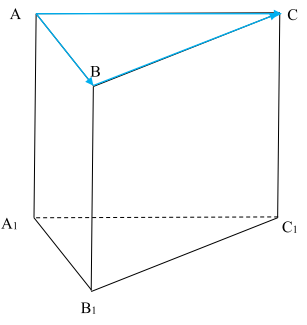
+ Dễ thấy:

\(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = \vec 0 \Rightarrow \vec b + \vec d - \vec c = \vec 0\)

Câu 8: Cho hình hộp ABCD.EFGH. Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Trong các khẳng định sau, khẳng định nào đúng?

A. \(\overrightarrow {BD} ,\overrightarrow {AK} ,\overrightarrow {GF} \) đồng phẳng.

B. \(\overrightarrow {BD} ,\overrightarrow {IK} ,\overrightarrow {GF} \) đồng phẳng.

C. \(\overrightarrow {BD} ,\overrightarrow {EK} ,\overrightarrow {GF} \) đồng phẳng.

D. \(\overrightarrow {BD} ,\overrightarrow {IK} ,\overrightarrow {GC} \) đồng phẳng.

Hướng dẫn giải

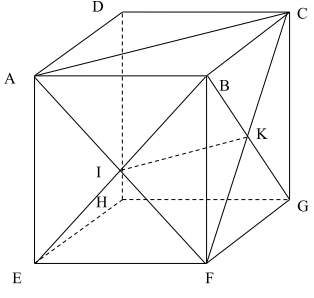
\( + \left\{ {\begin{array}{*{20}{l}}{IK//(ABCD)}\\{GF//(ABCD)}\\{{\rm{BD}} \subset ({\rm{ABCD}})}\end{array}} \right.\)

\( \Rightarrow \overrightarrow {IK} ,\overrightarrow {GF} ,\overrightarrow {BD} \)đồng phẳng

+ Các bộ vecto ở câu A, C, D không thể có giá cùng song song với một mặt phẳng.

Câu 9: Trong các khẳng định sau, khẳng định nào sai?

A. Nếu giá của ba vectơ \(\vec a,\vec b,\vec c\) cắt nhau từng đôi một thì ba vectơ đó đồng phẳng.

B. Nếu trong ba vectơ \(\vec a,\vec b,\vec c\) có một vectơ \(\vec 0\) thì ba vectơ đó đồng phẳng.

C. Nếu giá của ba vectơ \(\vec a,\vec b,\vec c\) cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.

D. Nếu trong ba vectơ \(\vec a,\vec b,\vec c\) có hai vectơ cùng phương thì ba vectơ đó đồng phẳng.

Hướng dẫn giải

+ Nắm vững khái niệm ba vecto đồng phẳng.

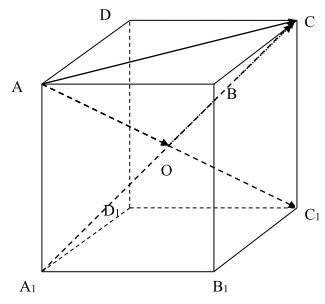
Câu 10: Cho hình hộp \(ABCD \cdot {A_1}{B_1}{C_1}{D_1}\). Trong các khẳng định sau, khẳng định nào saì?

A. \(\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = 2\overrightarrow {AC} \).

B. \(\overrightarrow {A{C_1}}  + \overrightarrow {C{A_1}}  + 2\overrightarrow {{C_1}C}  = \vec 0\).

C. \(\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = \overrightarrow {A{A_1}} \).

D. \(\overrightarrow {C{A_1}}  + \overrightarrow {AC}  = \overrightarrow {C{C_1}} \).

Hướng dẫn giải

+ Gọi O là tâm của hình hộp \(ABCD \cdot {A_1}{B_1}{C_1}{D_1}\).

+ Vận dụng công thức trung điểm để kiểm tra.

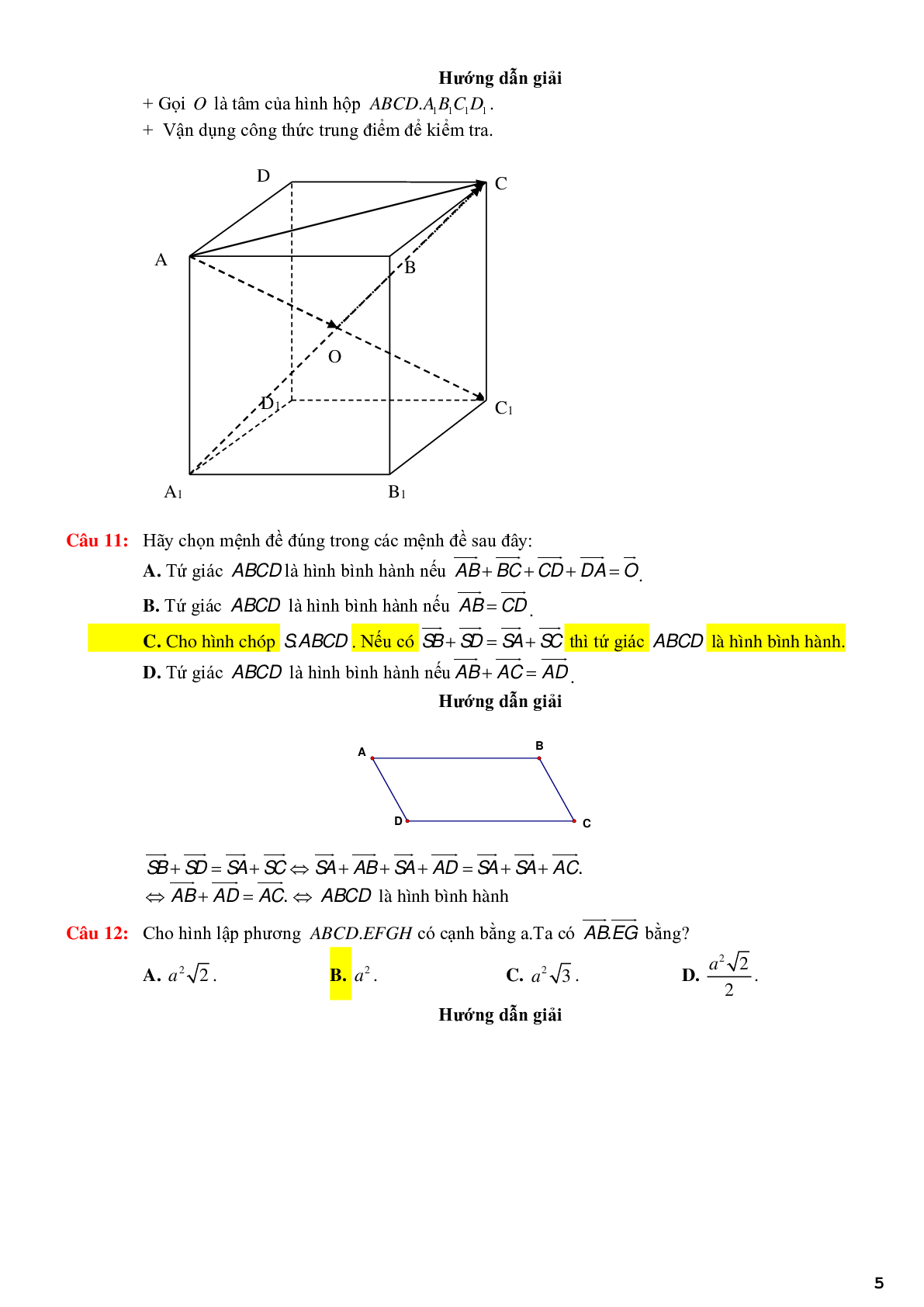
Câu 11: Hãy chọn mệnh đề đúng trong các mệnh đề sau đây:

A. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {DA}  = \vec O\).

B. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB}  = \overrightarrow {CD} \).

C. Cho hình chóp S.ABCD. Nếu có \(\overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SA}  + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành.

D. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \).

Hướng dẫn giải

\(\overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SA}  + \overrightarrow {SC}  \Leftrightarrow \overrightarrow {SA}  + \overrightarrow {AB}  + \overrightarrow {SA}  + \overrightarrow {AD}  = \overrightarrow {SA}  + \overrightarrow {SA}  + \overrightarrow {AC} \)

\( \Leftrightarrow \overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} . \Leftrightarrow ABCD\) là hình bình hàn

Câu 12: Cho hình lập phương ABCD.ÈGH có cạnh bằng a.Ta có \(\overrightarrow {AB}  \cdot \overrightarrow {EG} \) bằng?

A. \({a^2}\sqrt 2 \).

B. \({a^2}\).

C. \({a^2}\sqrt 3 \).

D. \(\frac{{{a^2}\sqrt 2 }}{2}\).

Hướng dẫn giải

$\begin{array}{l}\overrightarrow{AB}\cdot \overrightarrow{EG}=\overrightarrow{AB}\cdot (\overrightarrow{EF}+\overrightarrow{EH})\\ =\overline{AB}\cdot \overline{EF}+\overrightarrow{AB}\cdot \overline{EH}\\ ={\overrightarrow{AB}}^2+\overrightarrow{AB}\cdot \overrightarrow{AD}(\overrightarrow{EH}=\overrightarrow{AD})\\ =a^2(\text{ Vi}\overrightarrow{AB}\perp \overrightarrow{AD})\end{array}$