Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 40 câu trắc nghiệm Vận dụng cao Tích phân bám sát Đề minh họa THPTQG môn Toán năm 2021, tài liệu bao gồm 20 trang, 40 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

40 câu trắc nghiệm Vận dụng cao Tích phân bám sát Đề minh họa THPTQG môn Toán năm 2021 - có lời giải chi tiết

Câu 1: (Chuyên Lê Hồng Phong Nam Định 2019) Biết \(\int_1^4 f (x)dx = 5,\int_4^5 f (x)dx = 20\). Tính \(I = \int_1^2 f (4x - 3)dx - \int_0^{\ln 2} f \left( {{e^{2x}}} \right){e^{2x}}dx\)

A. \(I = \frac{{15}}{4}\).

B. \(I = 15\).

C. \(I = \frac{5}{2}\).

D. \(I = 25\).

Lời giải

Ta có

\(\int_1^5 f (x)dx = \int_1^4 f (x)dx + \int_4^5 f (x)dx = 25\)

\({I_1} = \int_1^2 f (4x - 3)dx\).

 Đặt \(u = 4x - 3 \Rightarrow du = 4dx \Rightarrow {I_1} = \int_1^5 {\frac{{f(u)}}{4}} du\)

\({I_2} = \int_0^{\ln 2} f \left( {{e^{2x}}} \right){e^{2x}}dx\).

 Đặt \(v = {e^{2x}} \Rightarrow dv = 2{e^{2x}}dx \Rightarrow {I_2} = \int_1^4 {\frac{{f(v)}}{2}} dv\)

\( \Rightarrow I = \frac{1}{4}\int_1^5 f (x)dx - \frac{1}{2}\int_1^4 f (x)dx = \frac{{25}}{4} - \frac{5}{2} = \frac{{15}}{4}\). Chọn A.

Câu 2: (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số y = f(x) liên tục trên \((0; + \infty )\) thỏa mãn \(2x{f^\prime }(x) + f(x) = 3{x^2}\sqrt x \). Biết \(f(1) = \frac{1}{2}\). Tính f(4).

A. 24 .

B. 14 .

C. 4 .

D. 16 .

Lời giải

Ta có:

\(\begin{array}{l}2x{f^\prime }(x) + f(x) = 3{x^2}\sqrt x \\ \Leftrightarrow \frac{{2x{f^\prime }(x)}}{{2\sqrt x }} + \frac{{f(x)}}{{2\sqrt x }} = \frac{{3{x^2}\sqrt x }}{{2\sqrt x }}\\ \Leftrightarrow {f^\prime }(x)\sqrt x  + \frac{{f(x)}}{{2\sqrt x }} = \frac{3}{2}{x^2}\end{array}\)

 \(\begin{array}{l} \Leftrightarrow {(f(x)\sqrt x )^\prime } = \frac{3}{2}{x^2}\\ \Leftrightarrow \int {(f(} x)\sqrt x {)^\prime }dx = \int {\frac{3}{2}} {x^2}dx\\ \Leftrightarrow f(x)\sqrt x  = \frac{{{x^3}}}{2} + C\end{array}\)

 \(f(1) = \frac{1}{2} \Rightarrow C = 0 \Rightarrow f(4) = 16\). Chọn D.

Câu 3: (Chuyên Đại học Vinh) Cho hàm số y = f(x) liên tục trên [0 ; 1] thỏa mãn \(\int_0^1 x f(x){\rm{d}}x = 0\) và \({\max _{[0;1]}}|f(x)| = 1\). Tích phân \(I = \int_0^1 {{{\rm{e}}^x}} f(x){\rm{d}}x\) thuộc khoảng nào trong các khoảng sau đây?

A. \(\left( { - \infty ; - \frac{5}{4}} \right)\).

B. \(\left( {\frac{3}{2};{\rm{e}} - 1} \right)\).

C. \(\left( { - \frac{5}{4};\frac{3}{2}} \right)\).

D. \(({\rm{e}} - 1; + \infty )\).

Lời giải

Với mọi \( \in [{\rm{0}};{\rm{1}}]{\rm{, }}\)

\({\rm{ta c\'o  0 = }}\int_{\rm{0}}^{\rm{1}} {\rm{x}} {\rm{f}}({\rm{x}}){\rm{dx = a}}\int_{\rm{0}}^{\rm{1}} {\rm{x}} {\rm{f}}({\rm{x}}){\rm{dx = }}\int_{\rm{0}}^{\rm{1}} {\rm{a}} {\rm{xf}}({\rm{x}}){\rm{dx}}{\rm{. }}\)

Kí hiệu: \({\rm{I}}({\rm{a}}){\rm{ = }}\int_{\rm{0}}^{\rm{1}} {\left( {{{\rm{e}}^{\rm{x}}}{\rm{ - ax}}} \right)} {\rm{dx}}{\rm{. }}\)

Khi đó, với mọi \(a \in [0;1]\) ta có :

\(\begin{array}{l}\left| {\int_0^1 {{{\rm{e}}^x}} f(x){\rm{d}}x} \right| = \left| {\int_0^1 {{{\rm{e}}^x}} f(x){\rm{d}}x - \int_0^1 a xf(x){\rm{d}}x} \right|\\ = \left| {\int_0^1 {\left( {{{\rm{e}}^x} - ax} \right)} f(x){\rm{d}}x} \right|\end{array}\)

\(\begin{array}{l} \le \int_0^1 {\left| {{{\rm{e}}^x} - ax} \right|}  \cdot |f(x)|{\rm{d}}x\\ \le \int_0^1 {\left| {{{\rm{e}}^x} - ax} \right|}  \cdot {\max _{x \in [0;1]}}|f(x)|{\rm{d}}x\\ = \int_0^1 {\left| {{{\rm{e}}^x} - ax} \right|} {\rm{d}}x = I(a)\\ \Rightarrow \left| {\int_0^1 {{{\rm{e}}^x}} f(x){\rm{d}}x} \right| \le {\min _{a \in [0;1]}}I(a)\end{array}\)

Mặt khác, với mọi \(a \in [0;1]\) ta có \(I(a) = \int_0^1 {\left| {{{\rm{e}}^x} - ax} \right|} {\rm{d}}x = \int_0^1 {\left( {{{\rm{e}}^x} - ax} \right)} {\rm{d}}x = \left. {\left( {{{\rm{e}}^x} - \frac{a}{2}{x^2}} \right)} \right|_0^1 = {\rm{e}} - \frac{a}{2} - 1\)

\({\min _{a \in [0;1]}}I(a) = {\rm{e}} - \frac{3}{2} \Rightarrow \left| {\int_0^1 {{{\rm{e}}^x}} f(x){\rm{d}}x} \right| \le {\rm{e}} - \frac{3}{2} \approx 1,22.\) Vậy \(I \in \left( { - \frac{5}{4};\frac{3}{2}} \right)\)

Chọn C

Câu 4. ( Chuyên Ngữ Hà nội ) Cho hàm số f(x) có đạo hàm \({f^\prime }(x)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^\prime }(x) \in [ - 1;1]\) với \(\forall x \in (0;2)\). Biết \(f(0) = f(2) = 1\). Đặt \(I = \int_0^2 f (x){\rm{d}}x\), phát biểu nào dưới đây đúng?

A. \(I \in ( - \infty ;0]\).

B. \(I \in (0;1]\).

C. \(I \in [1; + \infty )\).

D. \(I \in (0;1)\).

Lời giải: Ta có \(I = \int_0^2 f (x){\rm{d}}x = \int_0^1 f (x){\rm{d}}x + \int_1^2 f (x){\rm{d}}x\).

- \(\begin{array}{l}\int_0^1 f (x){\rm{d}}x = \left. {(x - 1)f(x)} \right|_0^1 - \int_0^1 {(x - 1)} {f^\prime }(x){\rm{d}}x\\ = 1 + \int_0^1 {(1 - x)} {f^\prime }(x){\rm{d}}x \ge 1 - \int_0^1 {(1 - x)} {\rm{d}}x = \frac{1}{2}(1)\end{array}\).

- \(\begin{array}{l}\int_1^2 f (x){\rm{d}}x = \left. {(x - 1)f(x)} \right|_1^2 - \int_1^2 {(x - 1)} {f^\prime }(x){\rm{d}}x\\ = 1 - \int_1^2 {(x - 1)} {f^\prime }(x){\rm{d}}x \ge 1 - \int_1^2 {(1 - x)} {\rm{d}}x = \frac{1}{2}(2)\end{array}\).

Từ (1) và \((2)\) suy ra \(I \ge \frac{1}{2} + \frac{1}{2} = 1\). Chọn C.

Câu 1: (Chuyên Ngữ Hà Nội) Cho F(x) là một nguyên hàm của hàm số \(f(x) = |1 + x| - |1 - x|\) trên tập \(\mathbb{R}\) và thỏa mãn F(1)= 3. Tính tổng \(F(0) + F(2) + F( - 3)\).

A. 8 .

B. 12 .

C. 14 .

D. 10 .

Lời giải: Bảng khử dấu giá trị tuyệt đối

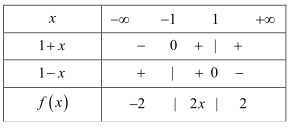
Ta có: \(\int_1^2 f (x){\rm{d}}x = F(2) - F(1) = F(2) - 3\)

mà \(\int_1^2 f (x){\rm{d}}x = \int_1^2 2 \;{\rm{d}}x = 2\) nên \(F(2) = 5\).

\( > \int_0^1 f (x){\rm{d}}x = F(1) - F(0) = 3 - F(0)\)

 mà \(\int_0^1 f (x){\rm{d}}x = \int_0^1 2 x\;{\rm{d}}x = \left. {{x^2}} \right|_0^1 = 1\) nên \(F(0) = 2\).

\( > \int_{ - 1}^0 f (x){\rm{d}}x = F(0) - F( - 1) = 2 - F( - 1)\)

mà \(\int_{ - 1}^0 f (x){\rm{d}}x = \int_{ - 1}^0 2 x\;{\rm{d}}x = \left. {{x^2}} \right|_{ - 1}^0 =  - 1\) nên \(F( - 1) = 3\).

\( > \int_{ - 3}^{ - 1} f (x){\rm{d}}x = F( - 1) - F( - 3) = 3 - F( - 3)\)

mà \(\int_{ - 3}^{ - 1} f (x){\rm{d}}x = \int_{ - 3}^{ - 1}  -  2\;{\rm{d}}x =  - 4\) nên \(F( - 3) = 7\).

Vậy \(F(0) + F(2) + F( - 3) = 2 + 5 + 7 = 14\). Chọn C.

Câu 5: (Sở Quảng Nam) Cho hàm số y = f(x) liên tục trên đoạn \(\left[ {0;\frac{\pi }{3}} \right]\). Biết \({f^\prime }(x)\cos x + f(x)\sin x = 1,\forall x \in \left[ {0;\frac{\pi }{3}} \right]\) và f(0)= 1. Tính tích phân \(I = \int_0^{\frac{\pi }{3}} f (x)dx\).

A. \(I = \frac{{\sqrt 3  + 1}}{2}\).

B. \(I = \frac{{\sqrt 3  - 1}}{2}\).

C. \(I = \frac{1}{2}\).

D. \(I = \frac{1}{2} + \frac{\pi }{3}\).

Lời giải Ta có:

\(\begin{array}{l}{f^\prime }(x)\cos x + f(x)\sin x = 1\\ \Leftrightarrow \frac{{{f^\prime }(x)}}{{\cos x}} + \frac{{f(x)\sin x}}{{{{\cos }^2}x}} = \frac{1}{{{{\cos }^2}x}}(\cos x \ne 0)\\ \Leftrightarrow {\left( {f(x) \cdot \frac{1}{{\cos x}}} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\end{array}\)

Nguyên hàm 2 vế ta được: \(f(x) \cdot \frac{1}{{\cos x}} = \int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C\)

\(f(0) = 1 \Rightarrow C = 1 \Rightarrow f(x) = \sin x + \cos x\)

\( \Rightarrow I = \frac{{\sqrt 3  + 1}}{2}.\) Chọn A.

Câu 1: (Toán học và tuổi trẻ - Lần 1) Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Biết \(\int_1^{{e^6}} {\frac{{f(\ln \sqrt x )}}{x}} dx = 6\) và \(\int_0^{\frac{\pi }{2}} f \left( {{{\cos }^2}x} \right)\sin 2xdx = 2\). Giá trị \(\int_1^3 {(f(} x) + 2)dx\) bằng?

A. 10 .

B. 16 .

C. 9 .

D. 5 .

Lời giải

Đặt \(t = {\cos ^2}x \Rightarrow dt =  - \sin 2xdx\), khi đó ta có: \(\int_0^{\frac{\pi }{2}} f \left( {{{\cos }^2}x} \right)\sin 2xdx = \int_0^1 f (t)dt \Rightarrow \int_0^1 f (t)dt = 2\)

\(\begin{array}{l}\int_1^3 f (t)dt = \int_0^3 f (t)dt - \int_0^1 f (t)dt = 1\\ \Rightarrow \int_1^3 {(f(} x) + 2)dx = \int_1^3 f (x)dx + \int_1^3 2 dx = 1 + 4 = 5.\end{array}\)

Chọn D

Câu 2: (Toán học tuổi trẻ 2019 – Lần 1) Cho hàm số f(x) liên tục trên đoạn [-1;1] và \(f( - x) + 2019f(x) = {2^x},\forall x \in [ - 1;1]\). Giá trị của \(\int_{ - 1}^1 f (x)dx\) là

A. \(\frac{1}{{2019\ln 2}}\)

B. \(\frac{3}{{4040\ln 2}}\)

C. 0

D. \(\frac{5}{{2018\ln 2}}\)

Lời giải

 Ta có: thay  x bởi (-x) vào phương trình: \(f(x) + 2019f( - x) = {2^{ - x}}\) nên ta có hệ :

\[\left\{ {\begin{array}{*{20}{l}}{f(x) + 2019f( - x) = {2^{ - x}}}\\{f( - x) + 2019f(x) = {2^x}}\end{array}} \right.\]

\[ \Rightarrow f(x) = \frac{{{{2019.2}^x}}}{{{{2019}^2} - 1}} - \frac{{{2^{ - x}}}}{{{{2019}^2} - 1}}\]

\(\begin{array}{l} \Rightarrow \int_{ - 1}^1 f (x)dx = \left. {\frac{{{{2019.2}^x}}}{{\left( {{{2019}^2} - 1} \right)\ln 2}}} \right|_{ - 1}^1 + \left. {\frac{{{2^{ - x}}}}{{\left( {{{2019}^2} - 1} \right)\ln 2}}} \right|_{ - 1}^1\\ = \frac{1}{{4040\ln 2}}{\rm{. }}\end{array}\)

Chọn B

Câu 3 ( Chuyên Bắc Ninh 2019) Cho hàm số f(x) thỏa mãn \({\left( {{f^\prime }(x)} \right)^2} + f(x){f^{\prime \prime }}(x) = {x^3} - 2x\) \(\forall x \in \mathbb{R}\) và \(f(0) = {f^\prime }(0) = 1\). Tính giá trị của \(T = {f^2}(2)\).

A. \(\frac{{43}}{{30}}\).

B. \(\frac{{16}}{{15}}\).

C. \(\frac{{43}}{{15}}\).

D. \(\frac{{26}}{{15}}\).

Lời giải

 Ta có

\(\begin{array}{l}{\left( {{f^\prime }(x)} \right)^2} + f(x){f^{\prime \prime }}(x) = {x^3} - 2x\\ \Leftrightarrow {\left( {f(x){f^\prime }(x)} \right)^\prime } = {x^3} - 2x\end{array}\)

Nguyên hàm 2 vế ta được: \(f(x){f^\prime }(x) = \frac{{{x^4}}}{4} - {x^2} + C\) mà \(f(0) = {f^\prime }(0) = 1 \Rightarrow C = 1\) \(\begin{array}{l} \Rightarrow f(x){f^\prime }(x) = \frac{{{x^4}}}{4} - {x^2} + 1\\ \Leftrightarrow \int f (x){f^\prime }(x)dx = \int {\frac{{{x^4}}}{4}}  - {x^2} + 1dx\\ \Leftrightarrow \int f (x)d(f(x)) = \int {\frac{{{x^4}}}{4}}  - {x^2} + 1dx\end{array}\)

 \( \Leftrightarrow \frac{{{f^2}(x)}}{2} = \frac{{{x^5}}}{{20}} - \frac{{{x^3}}}{3} + x + {C^\prime }\)

\( \Rightarrow {C^\prime } = \frac{1}{2} \Rightarrow {f^2}(2) = \frac{{43}}{{15}}\). Chọn \({\bf{C}}\).

Câu 1: (Chuyên Hạ Long Quảng Ninh - Lần 1 2019). Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) thoả mãn \({f^\prime }(x) + 2x \cdot f(x) = {e^{ - {x^2}}},\forall x \in \mathbb{R}\) và \(f(0) = 0\). Tính f(1).

A. \(f(1) = {e^2}\).

B. \(f(1) =  - \frac{1}{e}\).

C. \(f(1) = \frac{1}{{{e^2}}}\).

D. \(f(1) = \frac{1}{e}\).

Lời giải: Ta có

\(\begin{array}{l}{f^\prime }(x) + 2x \cdot f(x) = {e^{ - {x^2}}}\\ \Leftrightarrow {e^{{x^2}}} \cdot {f^\prime }(x) + 2x \cdot {e^{{x^2}}} \cdot f(x) = 1\end{array}\) \[\begin{array}{l} \Rightarrow \int_0^1 {\left[ {{e^{{x^2}}} \cdot {f^\prime }(x) + 2x \cdot {e^{{x^2}}} \cdot f(x)} \right]} dx = \left. {\int_0^1 d x \Leftrightarrow {e^{{x^2}}} \cdot f(x)} \right|_0^1 = 1\\ \Leftrightarrow f(1) = \frac{1}{e}.\end{array}\]

 Chọn D.

Câu 6: đH̛ờng sinh là nửa elip được cắt bởi trục lớn với 80cm, độ dài trục bé bằng 60cm và đáy trống kính bằng 60cm. Tính thể tích V của trống ( hàng đơn vị).

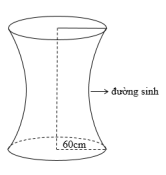
A. \(V = 344963\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\)

B. \(V = 344964\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).

C. \(V = 208347\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).

D. \(V = 208346\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\).

Lòi giải:

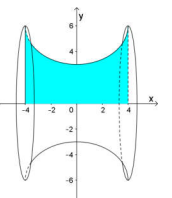
Đặt mặt phẳng qua trục của trống vào hệ tọa độ Oxy sao cho trục của trống trùng với trục hoành, trung điểm của trục đó là gốc tọa độ O. Ta xét đường sinh nằm trong mặt phẳng nói trên là một nửa của elip có tâm là I(0;6) và độ dài trục lớn là 8dm, độ dài trục nhỏ là 6dm.

Đường sinh đó thuộc elip có phương trình là \(\frac{{{x^2}}}{{16}} + \frac{{{{(y - 6)}^2}}}{9} = 1\).

Phương trình của đường sinh đó là: \(y = f(x) =  - 3\sqrt {1 - \frac{{{x^2}}}{{16}}}  + 6\).

Khi đó, trống là khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường sau quay quanh trục hoành: \(y = f(x),y = 0,x =  - 4,x = 4\).

Do đó, thể tích của trống bằng

 .

Suy ra:

\[\begin{array}{l}V = 9\pi \int_{ - 4}^4 {\left( {1 - \frac{{{x^2}}}{{16}} - 4\sqrt {1 - \frac{{{x^2}}}{{16}}}  + 4} \right)} dx\\ = 9\pi \int_{ - 4}^4 {\left( {5 - \frac{{{x^2}}}{{16}}} \right)} dx - 36\pi \int_{ - 4}^4 {\sqrt {1 - \frac{{{x^2}}}{{16}}} } dx\\ = \left. {9\pi \left( {5x - \frac{{{x^3}}}{{48}}} \right)} \right|_{ - 4}^4 - 36\pi \int_{ - 4}^4 {\sqrt {1 - \frac{{{x^2}}}{{16}}} } dx\end{array}\]

Suy ra

\(\begin{array}{l}\int_{ - 4}^4 {\sqrt {1 - \frac{{{x^2}}}{{16}}} } dx = \int_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\sqrt {1 - {{\sin }^2}t} } t.4\cos tdt\\ = \int_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} 4 {\cos ^2}tdt = 2\int_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {(1 + \cos 2t)} dt\\ = \left. {(2t + \sin 2t)} \right|_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} = 2\pi \end{array}\)

 Do đó

\(\begin{array}{l}V = 9\pi  \cdot \frac{{112}}{3} - 36\pi  \cdot 2\pi \\ \approx 344,9636147\left( {{\rm{d}}{{\rm{m}}^3}} \right) \approx 344964\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\end{array}\)

 Chọn B.

Câu 7: (THPT Quỳnh Lưu 1 - Nghệ An 2019). Cho hàm số f(x) thỏa mãn f(1)=2  và \({\left( {{x^2} + 1} \right)^2}{f^\prime }(x) = {[f(x)]^2}\left( {{x^2} - 1} \right)\) với mọi \(x \in \mathbb{R}\). Giá trị của f(2) bằng:

A. \(\frac{2}{5}\)

B. \( - \frac{2}{5}\)

C. \( - \frac{5}{2}\)

D. \(\frac{5}{2}\)

Lời giải

Ta có

\(\begin{array}{l}{\left( {{x^2} + 1} \right)^2}{f^\prime }(x) = {[f(x)]^2}\left( {{x^2} - 1} \right)\\ \Leftrightarrow \frac{{{f^\prime }(x)}}{{{{[f(x)]}^2}}} = \frac{{{x^2} - 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}\end{array}\)

\(\begin{array}{l} \Rightarrow \int_1^2 {\frac{{{f^\prime }(x)}}{{{{[f(x)]}^2}}}} dx = \int_1^2 {\frac{{{x^2} - 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}} dx\\ \Leftrightarrow \frac{1}{{f(1)}} - \frac{1}{{f(2)}} = \frac{1}{{10}} \Leftrightarrow f(2) = \frac{5}{2}\end{array}\)

 Chọn D.

Câu 8: (Sở GD Bắc Ninh - 2019). Cho hàm số f(x) liên tục trên \(\mathbb{R}\) thỏa mãn các điều kiện: \(f(0) = 2\sqrt 2 ,f(x) > 0,\forall x \in \mathbb{R}\) và \(f(x) \cdot {f^\prime }(x) = (2x + 1)\sqrt {1 + {f^2}(x)} ,\forall x \in \mathbb{R}\). Khi đó giá trị f(1) bằng:

A. \(\sqrt {15} \)

B. \(\sqrt {23} \)

C. \(\sqrt {24} \)

D. \(\sqrt {26} \)

Lời giải Ta có \(f(x) \cdot {f^\prime }(x) = (2x + 1)\sqrt {1 + {f^2}(x)}  \Leftrightarrow \frac{{f(x) \cdot {f^\prime }(x)}}{{\sqrt {1 + {f^2}(x)} }} = 2x + 1\).

Suy ra

\[\begin{array}{l}\int_0^1 {\frac{{f(x) \cdot {f^\prime }(x)}}{{\sqrt {1 + {f^2}(x)} }}} dx = \left. {\int_0^1 {(2x + 1)} dx \Leftrightarrow \sqrt {1 + {f^2}(x)} } \right|_0^1 = 2\\ \Leftrightarrow f(1) = \sqrt {24} \end{array}\]

 Chọn C.

Câu 9: (THPT Hậu Lộc 2 - Thanh Hóa) Cho hàm số f(x) nhận giá trị dương, và có đạo hàm liên tục trên đoạn [0 ; 1]. Biết f(1) = 1 và \(f(x)f(1 - x) = {e^{{x^2} - x}},\quad \forall x \in [0;1]\). Tính \(I = \int_0^1 {\frac{{\left( {2{x^3} - 3{x^2}} \right){f^\prime }(x)}}{{f(x)}}} dx?\)

A. \(I =  - \frac{1}{{60}}\).

B. \(I = \frac{1}{{10}}\).

C. \(I =  - \frac{1}{{10}}\).

D. \(I = \frac{1}{{60}}\).

Lời giải

Ta có

\(f(x)f(1 - x) = {e^{{x^2} - x}} \Rightarrow \ln f(x) + \ln f(1 - x) = {x^2} - x\)

Ta có: \(I = \int_0^1 {\frac{{\left( {2{x^3} - 3{x^2}} \right){f^\prime }(x)}}{{f(x)}}} dx\)

Đặt \(\left\{ {\begin{array}{*{20}{l}}{u = 2{x^3} - 3{x^2}}\\{dv = \frac{{{f^\prime }(x)}}{{f(x)}}dx}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{du = 6{x^2} - 6x}\\{v = \ln |f(x)| + C}\end{array}.} \right.} \right.\) Khi đó ta có:

\(\begin{array}{l}I = \left. {\left( {2{x^3} - 3{x^2}} \right)\ln f(x)} \right|_0^1 - 6\int_0^1 {\left( {{x^2} - x} \right)} \ln f(x)dx\\ =  - 6\int_0^1 {\left( {{x^2} - x} \right)} \ln f(x)dx\\ =  - 6\int_0^1 {\left( {{x^2} - x} \right)} \ln f(1 - x)dx\end{array}\)

Từ:

\[\begin{array}{l}\ln f(x) + \ln f(1 - x) = {x^2} - x\\ \Rightarrow I =  - 6\int_0^1 {\left( {{x^2} - x} \right)} \left( {\left( {{x^2} - x} \right) - \ln f(x)} \right)dx\end{array}\]

\(\begin{array}{l} =  - 6\int_0^1 {{{\left( {{x^2} - x} \right)}^2}} dx + 6\int_0^1 {\left( {{x^2} - x} \right)} \ln f(x)dx\\ \Rightarrow 12\int_0^1 {\left( {{x^2} - x} \right)} \ln f(x)dx = 6\int_0^1 {{{\left( {{x^2} - x} \right)}^2}} dx\\ \Rightarrow I =  - 6\int_0^1 {\left( {{x^2} - x} \right)} \ln f(x)dx =  - \frac{1}{{10}}{\rm{. }}\end{array}\)