Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển chọn các câu Vận dụng cao Số phức bám sát câu 47 đề minh họa THPTQG năm 2021, tài liệu bao gồm 101 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển chọn các câu Vận dụng cao Số phức bám sát câu 47 đề minh họa THPTQG năm 2021

Phần II Số phức

Chuyên đê: Số phức.

Xác định các yếu tố cơ bản

Lý thuyết

1. Phần thực, phần ảo của số phức, số phức liên hợp

- Số phức có dạng \(z = a + bi\left( {a,b \in R,{i^2} =  - 1} \right)\). Phần thực của z là a, phần ảo của z là b và i được gọi là đơn vị ảo.

- Số phức liên hợp của \(z\) là \(\bar z = \overline {a + bi}  = a - bi\).

\( \oplus z\bar z = {a^2} + {b^2}\)

\( \oplus \) Tổng và tích của z và \(\bar z\) luôn là một số thực.

\( \oplus \overline {{z_1} \pm {z_2}}  = \overline {{z_1}}  \pm \overline {{z_2}} .\)

\( \oplus \overline {{z_1} \cdot {z_2}}  = \overline {{z_1}}  \cdot \overline {{z_2}} .\)

\( \oplus \overline {\left( {\frac{{{z_1}}}{{{z_2}}}} \right)}  = \frac{{{{\bar z}_1}}}{{{{\bar z}_2}}}.\)

- Lưu ý: \({i^{4n}} = 1;{i^{4n + 1}} = i;{i^{4n + 2}} =  - 1;{i^{4n + 3}} =  - i\); với \(n \in N\).

2. Hai số phức bằng nhau

- Cho hai số phức \({z_1} = {a_1} + {b_1}i,{z_2} = {a_2} + {b_2}i\quad \left( {{a_1},{a_2},{b_2},{b_2} \in R} \right)\).

Khi đó: \({z_1} = {z_2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_1} = {a_2}}\\{{b_1} = {b_2}}\end{array}} \right.\)

3. Biểu diễn hình học của số phức, môđun của số phức

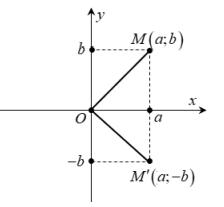
- Biễu diễn hình học của số phức.

- Số phức \(z = a + bi(a,b \in R)\) được biểu diễn bởi điểm M(a,b) trong mặt phẳng tọa độ.

- z và \(\bar z\) được biểu diễn bởi hai điểm đối xứng nhau qua trục Ox

+ Mô  đun của số phức z là \(|z| = |\overrightarrow {OM} | = \sqrt {{a^2} + {b^2}} \).

+ Ta có : \(|z| = \sqrt {z.\bar z} ;|z| = |\bar z|\).

Ví dụ minh họa

VÍ DỤ 1. Giải các phương trình sau:

a) \({3^{{x^2} - 4x + 5}} = 9\).

b) \({3^{{x^2} - 3x + 8}} = {9^{2x - 1}}\).

c) \({2^{\left| {\frac{{28}}{3}x + 4} \right|}} = {16^{{x^2} - 1}}\).

d) \({2^{8 - {x^2}}} \cdot {5^{8 - {x^2}}} = 0,001 \cdot {\left( {{{10}^5}} \right)^{1 - x}}\).

e) \({2^x} + {2^{x + 1}} = {3^x} + {3^{x + 1}}\).

f) \(12 \cdot {3^x} + {3.15^x} - {5^{x + 1}} = 20\).

Lời giải

Các câu hỏi trắc nghiệm lấy ra từ tài liệu

Câu 1: Cho số phức \(z = 1 - 2i\). Tìm phần ảo của số phức \(\bar z\).

A. 2 .

B. -2.

C. -1.

D. 1 .

Câu 2: Tìm các số thực x, y thỏa mãn \((3 - 2i)(x - yi) - 4(1 - i) = (2 + i)(x + yi)\)

A. \(x = 3,y =  - 1\).

B. \(x =  - 3,y =  - 1\).

C. \(x =  - 1,y = 3\).

D. \(x = 3,y = 1\).

Câu 3: Cho hai số phức \({z_1} = 2 + i,{z_2} = 1 - 3i\). Tính mô-đun của số phức \(w = z_1^2 - {z_2}\).

A. \(|w| = 7\).

B. \(|w| = 5\).

C. \(|w| = \sqrt {19} \).

D. \(|w| = \sqrt {53} \).

Câu 4: Cho số phức z thỏa mãn \(2z = i(\bar z + 3)\). Tính $|z|$.

A. \(|z| = 5\).

B. \(|z| = \frac{{3\sqrt 5 }}{2}\).

C. \(|z| = \sqrt 5 \).

D. \(|z| = \sqrt {10} \).

Câu 5: Cho số phức z thỏa mãn \(z + 2\bar z = 6 + 2i\). Điểm biểu diễn số phức \(z\) có tọa độ là

A. (2;-2).

B. (-2;-2).

C. (2;2).

D. (-2;2).

Câu 6: Tìm mô đun của số phức z, biết \(z - (2 + 3i)\bar z =  - 17 + 9i\).

A. \(|z| = \sqrt {26} \).

B. \(|z| = \sqrt {17} \).

C. \(|z| = \sqrt {29} \).

D. \(|z| = \sqrt 5 \).

Câu 7: Tìm tất cả các số thực x, y để hai số phức \({z_1} = 9{y^2} - 4 - 10x{i^5},{z_2} = 8{y^2} + 20{i^{11}}\) là hai số phức liên hợp của nhau.

A. \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y =  \pm 2}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x =  \pm 2}\\{y = 2}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x =  - 2}\\{y =  \pm 2}\end{array}} \right.\)

D. \(\left\{ {\begin{array}{*{20}{l}}{x =  - 2}\\{y = 2}\end{array}} \right.\).

Câu 8: Biết số phức z thỏa mãn. \(\left\{ {\begin{array}{*{20}{l}}{\left| {\frac{{z - 1}}{{z - i}}} \right| = 1}\\{\left| {\frac{{z - 3i}}{{z + i}}} \right| = 1}\end{array}} \right.\). Số phức \(\bar z\) bằng:

A. \(\bar z = 1 + i\).

B. \(\bar z = 1 - i\).

C. \(\bar z =  - 1 - i\).

D. \(\bar z =  - 1 + i\)

Câu 9: Tính môđun của số phức z, biết: \((1 - 2i)z + 2 - i =  - 12i\).

A. 5 .

B. \(\sqrt 7 \).

C. \(\frac{1}{2}\).

D. \(2\sqrt 2 \).

Câu 10: Nếu \(z = a + bi(a,b \in \mathbb{R})\) có số phức nghịch đảo \({z^{ - 1}} = \frac{{a - bi}}{4}\) thì

A. \({a^2} + {b^2} = 2\).

B. \({a^2} + {b^2} = 4\).

C. \({a^2} + {b^2} = 8\).

D. \({a^2} + {b^2} = 16\).

Câu 11: Cho số phức \(z = a + bi\) với \(a,b \in \mathbb{R}\) thỏa mãn \(z - 3 + i = |z|i\). Giá trị của a + b bằng

A. -1.

B. 7 .

C. 5 .

D. 12 .

Câu 12: Cho i là đơn vị ảo. Nghiệm của phương trình \(3z + i - 1 = \frac{{i + 2}}{{i - 2}}\) là

A. \(\frac{2}{{15}} - \frac{3}{5}i\).

B. \(\frac{2}{{15}} + \frac{3}{5}i\).

C. \( - \frac{2}{{15}} - \frac{2}{5}i\).

D. \( - \frac{2}{{15}} + \frac{3}{5}i\).

Câu 13: Có bao nhiêu số phức z thỏa mãn \({z^2} - 2018z = 2019|z{|^2}\) ?

A. Vô số.

B. 2 .

C. 1 .

D. 0 .

Câu 14: Có bao nhiêu số phức z thỏa mãn \({z^2} - 2018z = 2019|z{|^2}\) ?

A. Vô số.

B. 2 .

C. 1 .

D. 0 .

Câu 15: Cho hai số phức \(z = 3 - 4i\) và \({z^\prime } = (2 + m) + mi(m \in \mathbb{R})\) thỏa mãn \(\left| {{z^\prime }} \right| = |iz|\). Tổng tất cả các giá trị của m bằng

A. -1.

B. \(\frac{{\sqrt {46} }}{2}\).

C. 0 .

D. -2.

Câu 16: Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện: \(|z| = 1\) và \(\left| {{z^2} + 4} \right| = 2\sqrt 3 \).

A. 1 .

B. 2 .

C. 3 .

D. 4 .

Câu 17: Cho số phức \(z = a + bi(a,b \in \mathbb{R})\) thỏa mãn \(z + 2i\bar z = 3 + 3i\). Tính giá trị biểu thức:\(P = {(a + i)^{2019}} + {(b - i)^{2019}}{\rm{. }}\)

A. \( - {2^{1010}}\).

B. \( - {2^{1009}}\).

C. \( - {2^{1011}}\).

D. \( - {2^{1008}}\).

Câu 18: Có bao nhiêu số phức z thỏa mãn \(|z + i + 1| = |\bar z - 2i|\) và \(|z| = 1\)

A. 0 .

B. 2 .

C. 1 .

D. 4 .

Câu 19: Tìm hai số thực x và y thỏa mãn \((3x + 2yi) + (3 - i) = 4x - 3i\) với i là đơn vị ảo.

A. \(x = 3;y =  - 1\).

B. \(x = \frac{2}{3};y =  - 1\).

C. \(x = 3;y =  - 3\).

D. \(x =  - 3;y =  - 1\).

Câu 20: Có bao nhiêu số phức z thỏa mãn \({z^2} + 2|z| = 0\).

A. 1 .

B. 4 .

C. 2 .

D. 3 .

Câu 21: Với mọi số thuần ảo z, số \({z^2} + |z{|^2}\) là

A. số thực dương.

B. số thực âm.

C. số 0 .

D. số thuần ảo khác 0 .

Câu 22: Cho số phức \(z = 10 - 2i\). Phần thực và phần ảo của số phức \(\bar z\) là:

A. Phần thực bằng -10 và phần ảo bằng -2i. \(\quad \)

B. Phần thực bằng -10 và phần ảo bằng -2.

C. Phần thực bằng 10 và phần ảo bằng 2 .

D. Phần thực bằng 10 và phần ảo bằng 2i.

Câu 23: Cho số phức \(z = \frac{{(2 - 3i)(4 - i)}}{{3 + 2i}}\). Tìm tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy.

A. (1;4).

B. (-1;4).

C. (-1;-4).

D. (1;-4).

Câu 24: Cho số phức z có phần thực là số nguyên và z thỏa mãn \(|z| - 2\bar z =  - 7 + 3i + z\). Tính mô-đun của số phức \(\omega  = 1 - z + {z^2}\) bằng

A. \(|\omega | = \sqrt {37} \).

B. \(|\omega | = \sqrt {457} \).

C. \(|\omega | = \sqrt {425} \).

D. \(|\omega | = \sqrt {445} \).

Câu 25: Cho số phức \(z = a + bi(a,b \in \mathbb{R})\) thỏa mãn \(2|z| + \sqrt 3 iz = 4 - z\). Tính S = ab.

A. \(S = \frac{{\sqrt 3 }}{2}\).

B. \(S =  - \frac{{\sqrt 3 }}{2}\).

C. \(S = \frac{{\sqrt 3 }}{4}\).

D. \(S =  - \frac{{\sqrt 3 }}{4}\).

Câu 26: Cho số phức \(z = a + bi(a,b \in \mathbb{R},a > 0)\) thỏa \(z \cdot \bar z - 12|z| + (z - \bar z) = 13 + 10i\). Tính S = a+ b.

A. S = 7

B. S = 17.

C. S = -17.

D. S = 5.

Câu 27: Có bao nhiêu số phức z thỏa mãn \(|z{|^2} = 2|z + \bar z| + 4\) và \(|z - 1 - i| = |z - 3 + 3i|\) ?

A. 4 .

B. 3 .

C. 1 .

D. 2 .

Câu 28: Cho hai số phức z và w khác 0 thoả mãn \(|z + 3w| = 5|w|\) và \(|z - 2wi| = |z - 2w - 2wi|\). Phần thực của số phức \(\frac{z}{w}\) bằng

A. 1 .

B. \( - 3\).

C. \( - 1\).

D. 3 .

Câu 29: Cho số phức z thoả mãn \(2|z + 1{|^2} = |z - i{|^2}\). Tính môđun của số phức \(z + 2 + i\).

A. 1 .

B. 3 .

C. 4 .

D. 2 .

Câu 30: Số phức \(z = a + bi,a,b \in \mathbb{R}\) là nghiệm của phương trình \(\frac{{(|z| - 1)(1 + iz)}}{{z - \frac{1}{z}}} = i\). Tổng \(T = {a^2} + {b^2}\) bằng

A. 4 .

B. \(4 - 2\sqrt 3 \).

C. \(3 + 2\sqrt 2 \).

D. 3 .

Câu 31: Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại 2 số phức phân biệt \({z_1},{z_2}\) thỏa mãn đồng thời các phương trình \(|z - 1| = |z - i|\) và \(|z + 2m| = m + 1\). Tổng tất cả các phần tử của S là

A. 1 .

B. 4 .

C. 2 .

D. 3 .

Câu 32: Gọi S là tập hợp tất cả các số m sao cho tồn tại đúng một số phức z thỏa mãn đồng thời các phương trình \(|z + 2 + i| = |z + 1|\) và \(\sqrt 2 |z - 3 + 2i| = {m^2} - 5m + 9\). Tích tất cả các phần tử của S là

A. 6 .

B. 5 .

C. 2 .

D. 3 .

Câu 33: Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại 2 số phức phân biệt \({z_1},{z_2}\) thỏa mãn đồng thời các phương trình \(|(3 + 4i)z + 25| = 20\) và \(|z + m + 2i| = 5\). Số các phần tử của S là

A. 8 .

B. 7 .

C. 6 .

D. 5 .

Câu 34: Trên mặt phẳng phức, tập hợp điểm biểu diễn số phức z thỏa mãn \(|z + (2 - 3i)| = 2\) là đường tròn có phương trình nào sau đây?

A. \({x^2} + {y^2} - 4x - 6y + 9 = 0\).

B. \({x^2} + {y^2} - 4x + 6y + 11 = 0\).

C. \({x^2} + {y^2} - 4x - 6y + 11 = 0\).

D. \({x^2} + {y^2} + 4x - 6y + 9 = 0\).

Câu 35: Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn có tâm \({\rm{O}}\), bán kính bằng 5 và nằm trên đường thẳng \(d:x - 2y + 5 = 0\).

A. \(z = 3 - 4i\).

B. \(z = 3 + 4i\).

C. \(z = 4 + 3i\).

D. \(z = 4 - 3i\).

Câu 36: Cho số thực x, y thỏa mãn \((2x + yi) + (3 - 2i)(x + y) = 1\), với i là đơn vị ảo là

A. \(x = 1,y =  - 2\).

B. \(x = 2,y =  - 1\).

C. \(x =  - 1,y = 2\).

D. \(x =  - 2,y = 1\)

Câu 37: Cho số phức \(z = m + 3 + \left( {{m^2} - m - 6} \right)i\) với \(m \in \mathbb{R}\). Gọi (P) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng

A. \(\frac{{125}}{6}\).

B. \(\frac{{17}}{6}\).

C. 1 .

D. \(\frac{{55}}{6}\).

Câu 38: Cho các số phức z thỏa mãn \(|z + 1| = 2\). Biết rằng tập hợp các điểm biểu diễn các số phức \(w = (1 + i\sqrt 8 )z + i\) là một đường tròn. Bán kính r của đường tròn đó là

A. 9 .

B. 36 .

C. 6 .

D. 3 .

Câu 39: Gọi \({z_1},{z_2}\) là hai trong các số phức thỏa mãn \(|z - 1 + 2i| = 5\) và \(\left| {{z_1} - {z_2}} \right| = 8\). Tìm mô đun của số phức \(w = {z_1} + {z_2} - 2 + 4i\).

A. \(|w| = 6\).

B. \(|w| = 10\).

C. \(|w| = 16\).

D. \(|w| = 13\).

Câu 40: Cho số phức z thoả mãn \(|z - 1| \le 1\) và \(z - \bar z\) có phần ảo không âm. Tập hợp các điểm biểu diễn số phức z là một miền phẳng. Tính diện tích S của miền phẳng này

A. \(S = \pi \).

B. \(S = 2\pi \).

C. \(S = \frac{1}{2}\pi \).

D. \(S = 1\).

Câu 41: Cho số phức \(z = m + \left( {{m^3} - m} \right)i\), với m là tham số thực thay đổi. Tập hợp tất cả các điểm biểu diễn số phức z là đường cong (C ). Tính diện tích hình phẳng giới hạn bởi (C ) và trục hoành.

A. \(\frac{1}{2}\).

B. \(\frac{1}{4}\).

C. \(\frac{3}{4}\).

D. \(\frac{3}{2}\).

Câu 42: Phần gạch trong hình vẽ dưới là hình biểu diễn của tập các số phức thỏa mãn điều kiện nào sau đây?

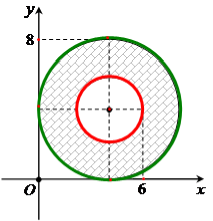
A. \(6 \le |z| \le 8\).

B. \(2 \le |z + 4 + 4i| \le 4\).

C. \(2 \le |z - 4 - 4i| \le 4\).

D. \(4 \le |z - 4 - 4i| \le 16\).