Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Áp dụng đẳng thức và bất đẳng thức mô đun tìm GTLN – GTNN của mô đun số phức, tài liệu bao gồm 14 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
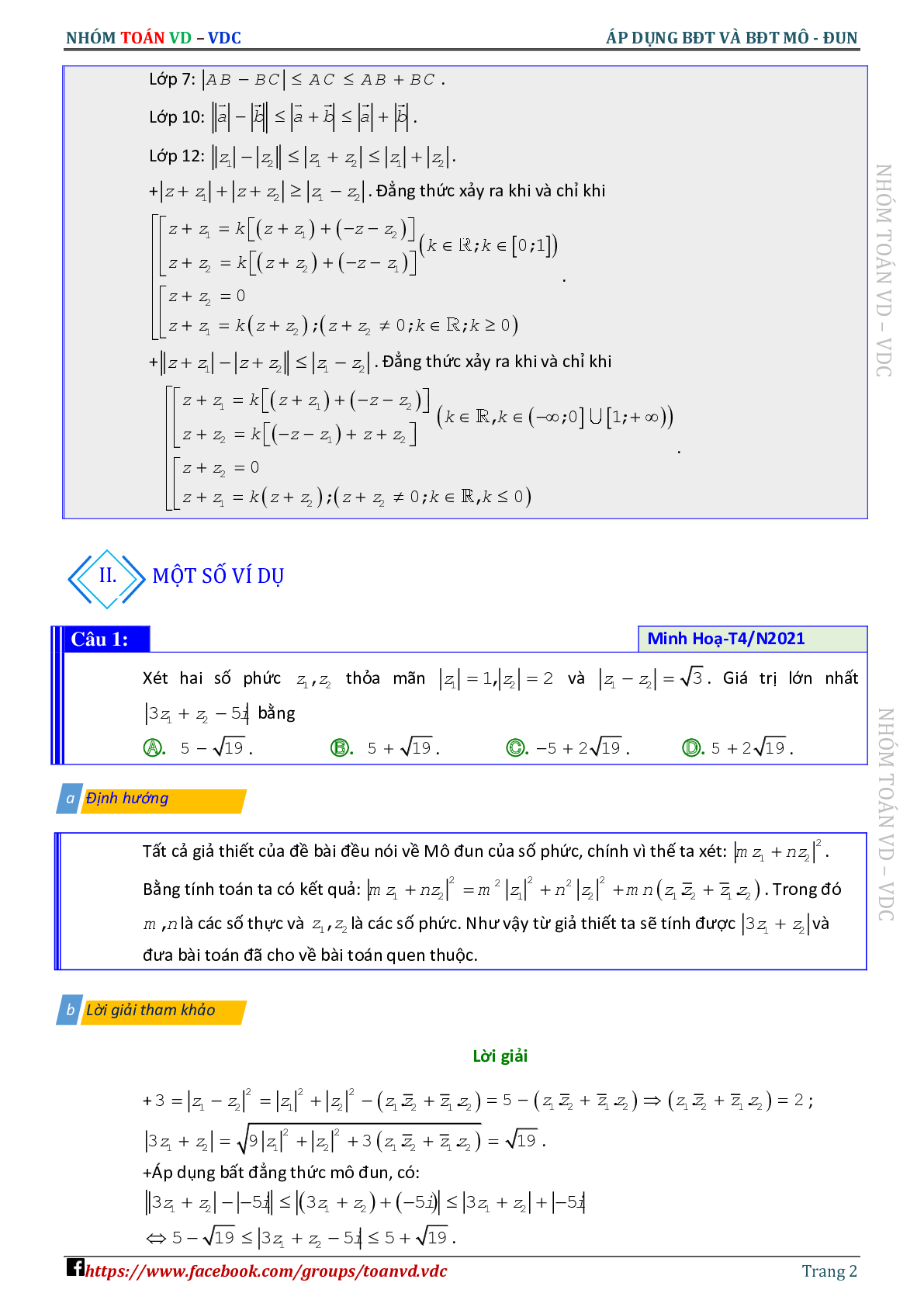
I. Lý thuyết
Mỗi số phức, ở khía cạnh đại số, là nghiệm tương ứng duy nhất một tam thức bậc hai monic hệ số thực có biệt thức âm. Nếu z là nghiệm của 2 f x x ax b với a b và 2 a b4 0 thì nghiệm còn lại sẽ gọi là liên hợp của nó. Tích hai nghiệm sẽ là b và là một số không âm. Căn bậc hai của b gọi là module. Ở khía cạnh hình học, mỗi số phức sẽ là cặp tọa độ của một vector, và độ lớn của vector đó chính là module. Module của số phức. Số phức liên hợp.
1. Đẳng thức Mô đun.
2. Bất đẳng thức Mô đun.
II. Ví dụ minh họa
III. Bài tập tương tự
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
