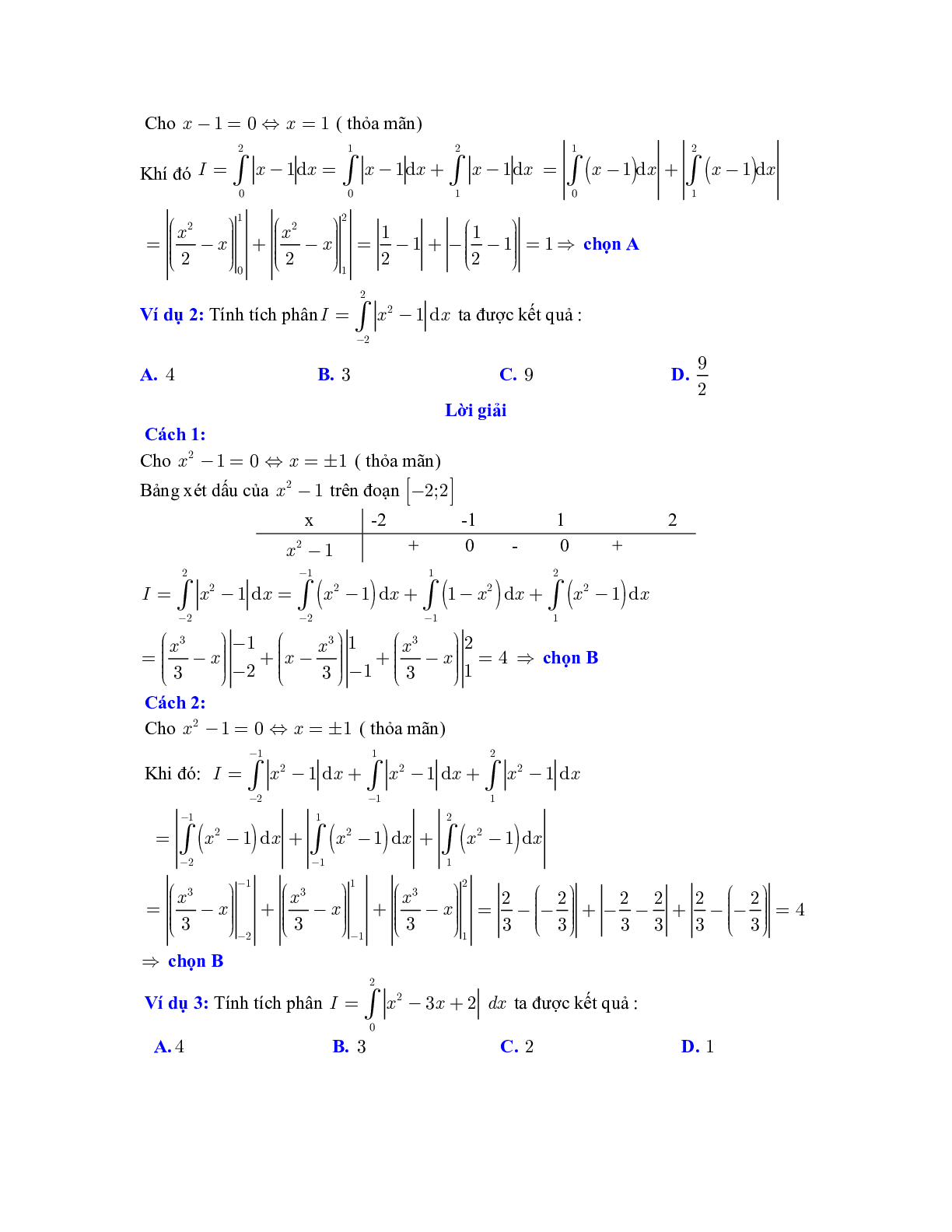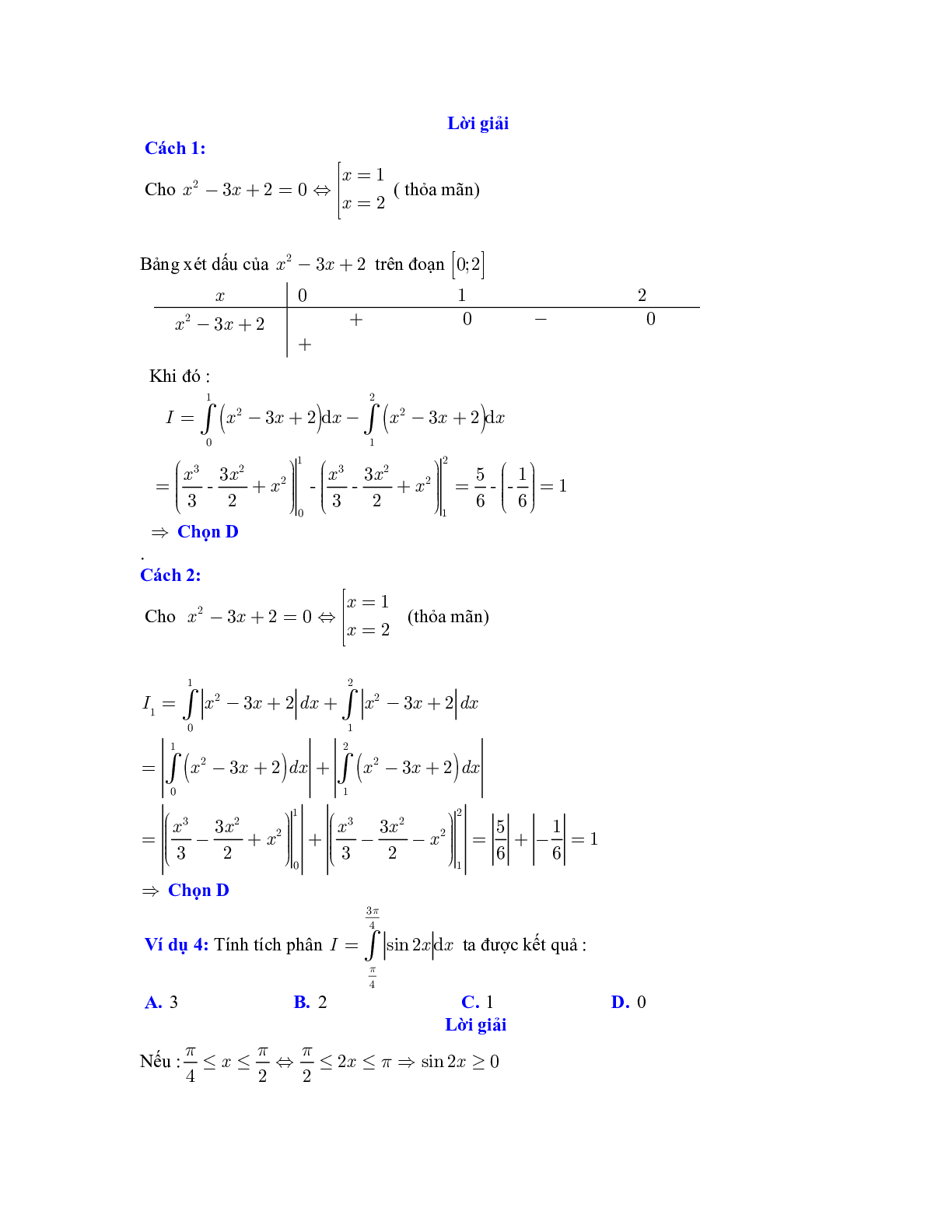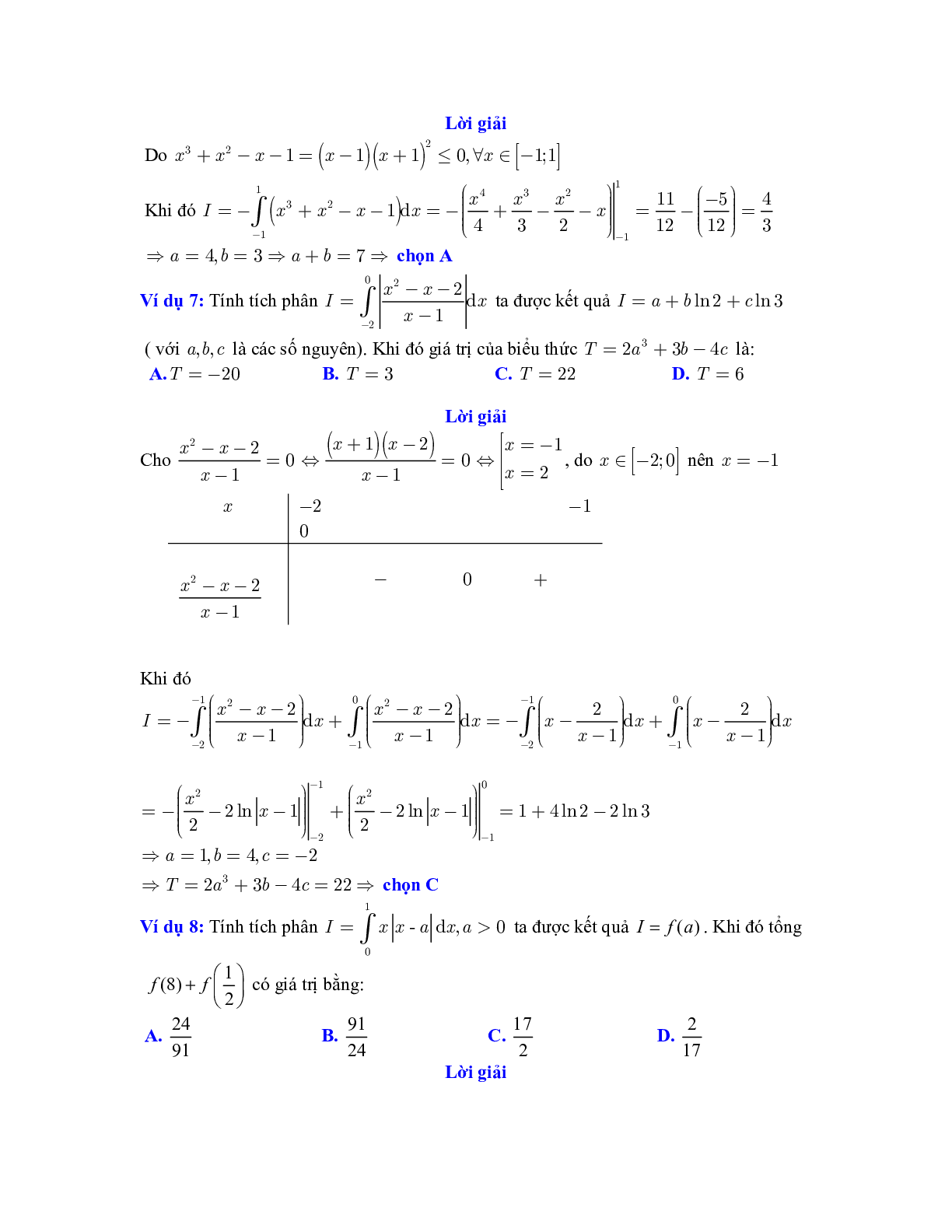Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập Vận dụng cao - Tích phân chứa dấu giá trị tuyệt đối ôn thi THPTQG năm 2021, tài liệu bao gồm 9 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Lý thuyết và bài tập Vận dụng cao - Tích phân chứa dấu giá trị tuyệt đối ôn thi THPTQG năm 2021

Chương III: Nguyên hàm tích phân và ứng dụng

Bài 2: Tích phân

I . Lý thuyết

1. Đinh nghĩa: Cho hàm số f(x) liên tục trên đoạn [a ; b]. Hàm số F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a ; b]. Hiệu số F(b) – F(a) được gọi là tích phân tù̀ a đến b của hàm số f(x). Kí hiệu: \(\int_a^b f (x)dx\).

Vậy: \(\int_a^b f (x)dx = \left. {F(x)} \right|_a^b = F(b) - F(a)\)

Ta gọi \(\mathop \smallint \nolimits_a^b \) là dấu tích phân; a là cận dưới; b là cận trên; f(x) là hàm số dưới dấu tích phân; f(x) dx là biểu thức dưới dấu tích phân.

Chú ý:

a) \(\int_a^a f (x)dx = 0.\int_a^b f (x)dx =  - \int_b^a f (x)dx\).

b) Tích phân chỉ phụ thuộc vào hàm f và các cận a, b mà không phụ thuộc vào biến:

\(\int_a^b f (x)dx = \int_a^b f (t)dt\)

2. Các tính chất của tích phân:

Tính chất 1: \(\quad \int_a^b k  \cdot f(x)dx = k \cdot \int_a^b f (x)dx\).

Tính chất 2: \(\quad \int_a^b {(f(} x) \pm g(x))dx = \int_a^b f (x)dx \pm \int_a^b g (x)dx\).

Tính chất 3: \(\quad \int_a^b f (x)dx = \int_a^c f (x)dx + \int_c^b f (x)dx\quad ,\quad (a < c < b)\).

II Dạng toán

Tích phân của hàm số có chứa dấu giá trị tuyệt đối

Bài toán : Tính tích phân \(I = \int_a^b g (x){\rm{d}}x\)

(với g(x) là biểu thức chứa ẩn trong dấu giá trị tuyệt đối)

PP chung:

Xét dấu của biểu thức trong dấu giá trị tuyệt đối trên [a ; b]

Dựa vào dấu để tách tích phân treeb mỗi đoạn tương ứng ( sử dụng tính chất 3 để tách)

Tính mỗi tích phân thành phần.

Đặc biệt

Tính tích phân

Cách giải

Cách 1

+ Cho f(x)=0 tìm nghiệm trên [a ; b]

+ Xét dấu của f(x) trên [a ; b], dụa vào dấu của f(x) để tách tích phân trên mô̂i đoạn tương ứng (sử dụng tính chất 3 để tách)

+) Tính mối tích phân thành phần.

Cách 2:

+) Cho f(x) = 0 tìm nghiệm trên [a ; b] giả sử các nghiệm đó là \({x_1};{x_2}; \ldots {x_n}\)

( với \({x_1} < {x_2} <  \ldots  < {x_n}\) ).

Khi đó

\(\begin{array}{l}I = \int_a^{{x_1}} | f(x)|{\rm{d}}x + \int_{{x_1}}^{{x_2}} | f(x)|{\rm{d}}x + \int_{{x_2}}^{{x_3}} | f(x)|{\rm{d}}x +  \ldots  + \int_{{x_n}}^b | f(x)|{\rm{d}}x\\ \Rightarrow I = \left| {\int_a^{{x_1}} f (x){\rm{d}}x} \right| + \left| {\int_{{x_1}}^{{x_2}} f (x){\rm{d}}x} \right| + \left| {\int_{{x_2}}^{{x_3}} f (x){\rm{d}}x} \right| +  \ldots  + \left| {\int_{{x_n}}^b f (x){\rm{d}}x} \right|\end{array}\)

+) Tính mối tích phân thành phần

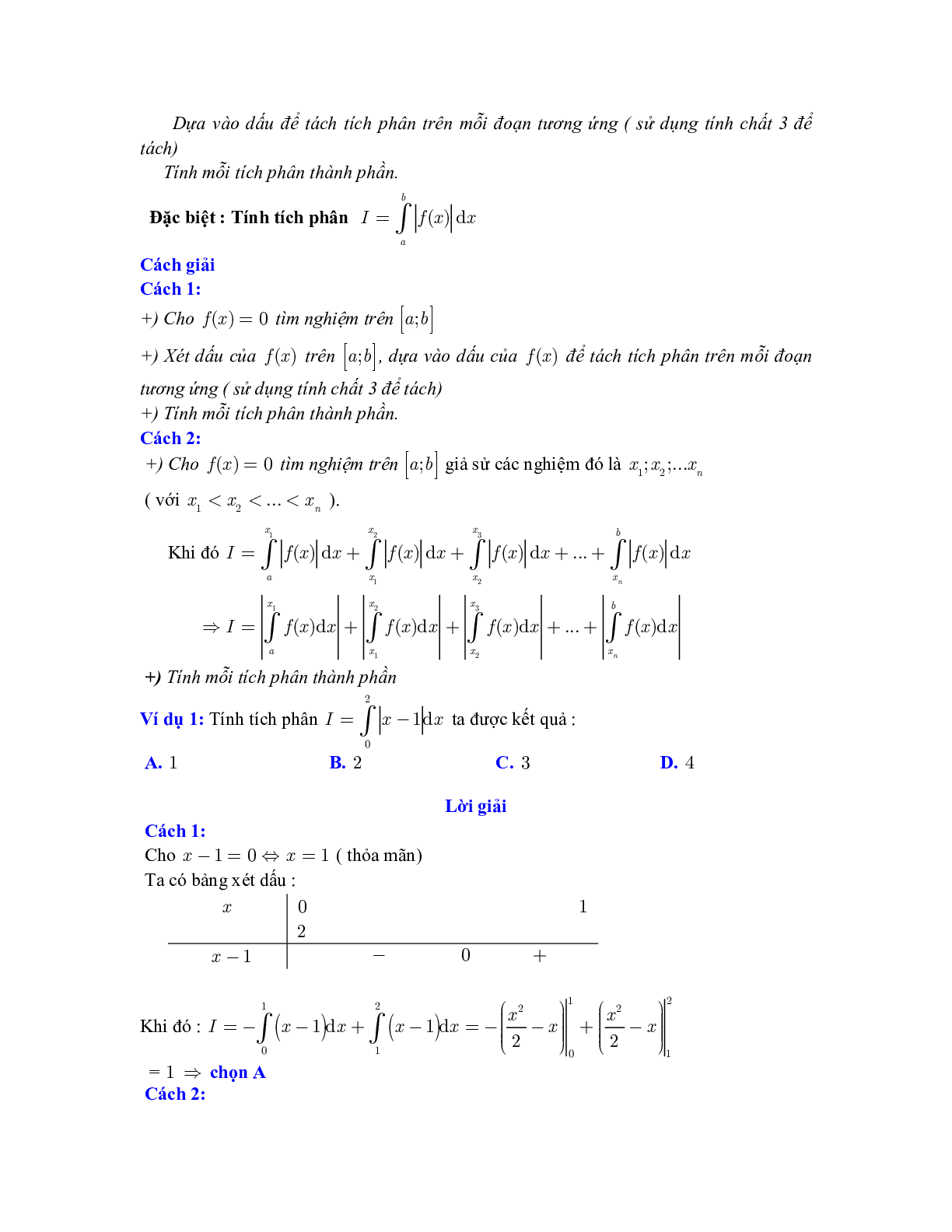
Ví dụ 1: Tính tích phân \(I = \int_0^2 | x - 1|{\rm{d}}x\) ta được kết quả :

A. 1

B. 2

C. 3

D. 4

Lời giải

Cách 1:

Cho \(x - 1 = 0 \Leftrightarrow x = 1\) ( thỏa mãn)

Ta có bảng xét dấu :

Khi đó:

\(\begin{array}{l}I =  - \int_0^1 {(x - 1)} {\rm{d}}x + \int_1^2 {(x - 1)} {\rm{d}}x\\ =  - \left. {\left( {\frac{{{x^2}}}{2} - x} \right)} \right|_0^1 + \left. {\left( {\frac{{{x^2}}}{2} - x} \right)} \right|_1^2 = {\rm{ }}1\end{array}\)

Chọn A

Cách 2:

Cho \(x - 1 = 0 \Leftrightarrow x = 1\) ( thỏa mãn)

\[\begin{array}{l}{\rm{ }}I = \int_0^2 | x - 1|{\rm{d}}x = \int_0^1 | x - 1|{\rm{d}}x + \int_1^2 | x - 1|{\rm{d}}x\\ = \left| {\int_0^1 {(x - 1)} {\rm{d}}x} \right| + \left| {\int_1^2 {(x - 1)} {\rm{d}}x} \right|\\ = \left. {\left| {\left( {\frac{{{x^2}}}{2} - x} \right)} \right|_0^1| + |\left( {\frac{{{x^2}}}{2} - x} \right)} \right|_1^2|\\ = |\frac{1}{2} - 1| + | - \left| {\frac{1}{2} - 1} \right| = 1\end{array}\]

Chọn A

Ví dụ 2: Tính tích phân \(I = \int_{ - 2}^2 {\left| {{x^2} - 1} \right|} {\rm{d}}x\) ta được kết quả :

A. 4

B. 3

C. 9

D. \(\frac{9}{2}\)

Lời giải

Cách 1:

Cho \({x^2} - 1 = 0 \Leftrightarrow x =  \pm 1\) ( thỏa mãn)

Bảng xét dấu của \({x^2} - 1\) trên đoạn \([ - 2;2]\)

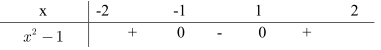
Cách 2:

Cho \({x^2} - 1 = 0 \Leftrightarrow x =  \pm 1\) ( thỏa mãn)

Khi đó: \(I = \int_{ - 2}^{ - 1} {\left| {{x^2} - 1} \right|} {\rm{d}}x + \int_{ - 1}^1 {\left| {{x^2} - 1} \right|} {\rm{d}}x + \int_1^2 {\left| {{x^2} - 1} \right|} {\rm{d}}x\)

\( = \left| {\int_{ - 2}^{ - 1} {\left( {{x^2} - 1} \right)} {\rm{d}}x} \right| + \left| {\int_{ - 1}^1 {\left( {{x^2} - 1} \right)} {\rm{d}}x} \right| + \left| {\int_1^2 {\left( {{x^2} - 1} \right)} {\rm{d}}x} \right|\)

\(\begin{array}{l} = \left. {\left. {\left| {\left( {\frac{{{x^3}}}{3} - x} \right)} \right|_{ - 2}^{ - 1}| + |\left( {\frac{{{x^3}}}{3} - x} \right)} \right|_{ - 1}^1| + |\left( {\frac{{{x^3}}}{3} - x} \right)} \right|_1^2|\\ = |\frac{2}{3} - \left( { - \frac{2}{3}} \right)| + | - \frac{2}{3} - \frac{2}{3}| + |\frac{2}{3} - \left( { - \frac{2}{3}} \right)\mid  = 4\end{array}\)

\( \Rightarrow \) chọn B

Ví dụ 3: Tính tích phân \(I = \int_0^2 {\left| {{x^2} - 3x + 2} \right|} dx\) ta được kết quả :

A. 4

B. 3

C. 2

D. 1

Lời giải

Cách 1:

Cho \({x^2} - 3x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 2}\end{array}} \right.\) ( thỏa mãn)

Bảng xét dấu của \({x^2} - 3x + 2\) trên đoạn [0 ; 2]

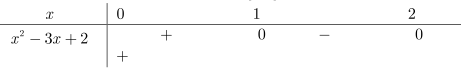
Khi đó :

\(\begin{array}{l}I = \int_0^1 {\left( {{x^2} - 3x + 2} \right)} {\rm{d}}x - \int_1^2 {\left( {{x^2} - 3x + 2} \right)} {\rm{d}}x\\ = \left. {\left( {\frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} + {x^2}} \right)} \right|_0^1 - \left. {\left( {\frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} + {x^2}} \right)} \right|_1^2 = \frac{5}{6} - \left( { - \frac{1}{6}} \right) = 1\end{array}\)

Chọn D

Cách 2:

Cho \({x^2} - 3x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 2}\end{array}} \right.\) (thỏa mãn)

\[\begin{array}{l}{I_1} = \int_0^1 {\left| {{x^2} - 3x + 2} \right|} dx + \int_1^2 {\left| {{x^2} - 3x + 2} \right|} dx\\ = \left| {\int_0^1 {\left( {{x^2} - 3x + 2} \right)} dx} \right| + \left| {\int_1^2 {\left( {{x^2} - 3x + 2} \right)} dx} \right|\\ = \left| {\left( {\frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} + {x^2}} \right)} \right|_0^1 + \left| {\left( {\frac{{{x^3}}}{3} - \frac{{3{x^2}}}{2} - {x^2}} \right)} \right|_1^2\\ = \left| {\frac{5}{6}} \right| + \left| { - \frac{1}{6}} \right| = 1\end{array}\]

\( \Rightarrow \) Chọn D

Ví dụ 4: Tính tích phân \(I = \int_{\frac{\pi }{4}}^{\frac{{3\pi }}{4}} | \sin 2x|{\rm{d}}x\) ta được kết quả :

A. 3

B. 2

C. 1

D. 0

Lời giải

Nếu \(:\frac{\pi }{4} \le x \le \frac{\pi }{2} \Leftrightarrow \frac{\pi }{2} \le 2x \le \pi  \Rightarrow \sin 2x \ge 0\)

Nếu \(:\frac{\pi }{2} \le x \le \frac{{3\pi }}{4} \Leftrightarrow \pi  \le 2x \le \frac{{3\pi }}{2} \Rightarrow \sin 2x \le 0\)

Khi đó: \(I = \int_{\frac{\pi }{4}}^{\frac{{3\pi }}{4}} | \sin 2x|{\rm{d}}x = \int_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\sin } 2x\;{\rm{d}}x - \int_{\frac{\pi }{2}}^{\frac{{3\pi }}{4}} {\sin } 2x\;{\rm{d}}x\)

\(\begin{array}{l} =  - \left. {\frac{1}{2}\cos 2x} \right|_{\frac{\pi }{4}}^{\frac{\pi }{2}} + \left. {\frac{1}{2}\cos 2x} \right|_{\frac{\pi }{2}}^{\frac{{3\pi }}{4}}\\ =  - \frac{1}{2}( - 1 - 0) + \frac{1}{2}(0 + 1) = 1\end{array}\)

\( \Rightarrow \) Chọn \({\bf{C}}\)

Ví dụ 5: Tính tích phân \(I = \int_{ - 1}^a {\left| {{x^2} - x} \right|} {\rm{d}}x\) ta được kết quả \(I = \frac{{11}}{6}\), khi đó ta có:

A. a = 1

B. a = 2

C. a = 3

D. a =  4

Nhận xét: tù các đáp án \( \Rightarrow a \ge 1\)

Lời giải

Cho \({x^2} - x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array}} \right.\) ( thỏa mãn)

Ta có bảng xét dấu của \({x^2} - x\) trên đoạn \([ - 1;a]\)

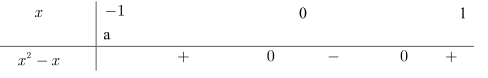
Khi đó \(I = \int_{ - 1}^0 {\left( {{x^2} - x} \right)} {\rm{d}}x - \int_0^1 {\left( {{x^2} - x} \right)} {\rm{d}}x + \int_1^a {\left( {{x^2} - x} \right)} {\rm{d}}x\)

\(\begin{array}{l}\left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)} \right|_{ - 1}^0 - \left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)} \right|_0^1 + \left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)} \right|_1^a\\ = 0 - \left( { - \frac{5}{6}} \right) - \left( { - \frac{1}{6}} \right) + \left( {\frac{{{a^3}}}{3} - \frac{{{a^2}}}{2}} \right) - \left( { - \frac{1}{6}} \right)\end{array}\)

\( = \frac{7}{6} + \frac{{{a^3}}}{3} - \frac{{{a^2}}}{2}\)

Do

\(I = \frac{{55}}{{30}} \Leftrightarrow \frac{7}{6} + \frac{{{a^3}}}{3} - \frac{{{a^2}}}{2} = \frac{{11}}{6} \Leftrightarrow 2{a^3} - 3{a^2} - 4 = 0\)

\( \Leftrightarrow (a - 2)\left( {2{a^2} + a + 2} \right) = 0 \Rightarrow a = 2\)

\( \Rightarrow \) chọn B

Ví dụ 6: Tính tích phân \(I = \int_{ - 1}^1 {\left| {{x^3} + {x^2} - x - 1} \right|} {\rm{d}}x\) ta được kết quả \(I = \frac{a}{b}\), khi đó tổng \(a + b\) là:

A. 7

B. 3

C. 5

D. 9