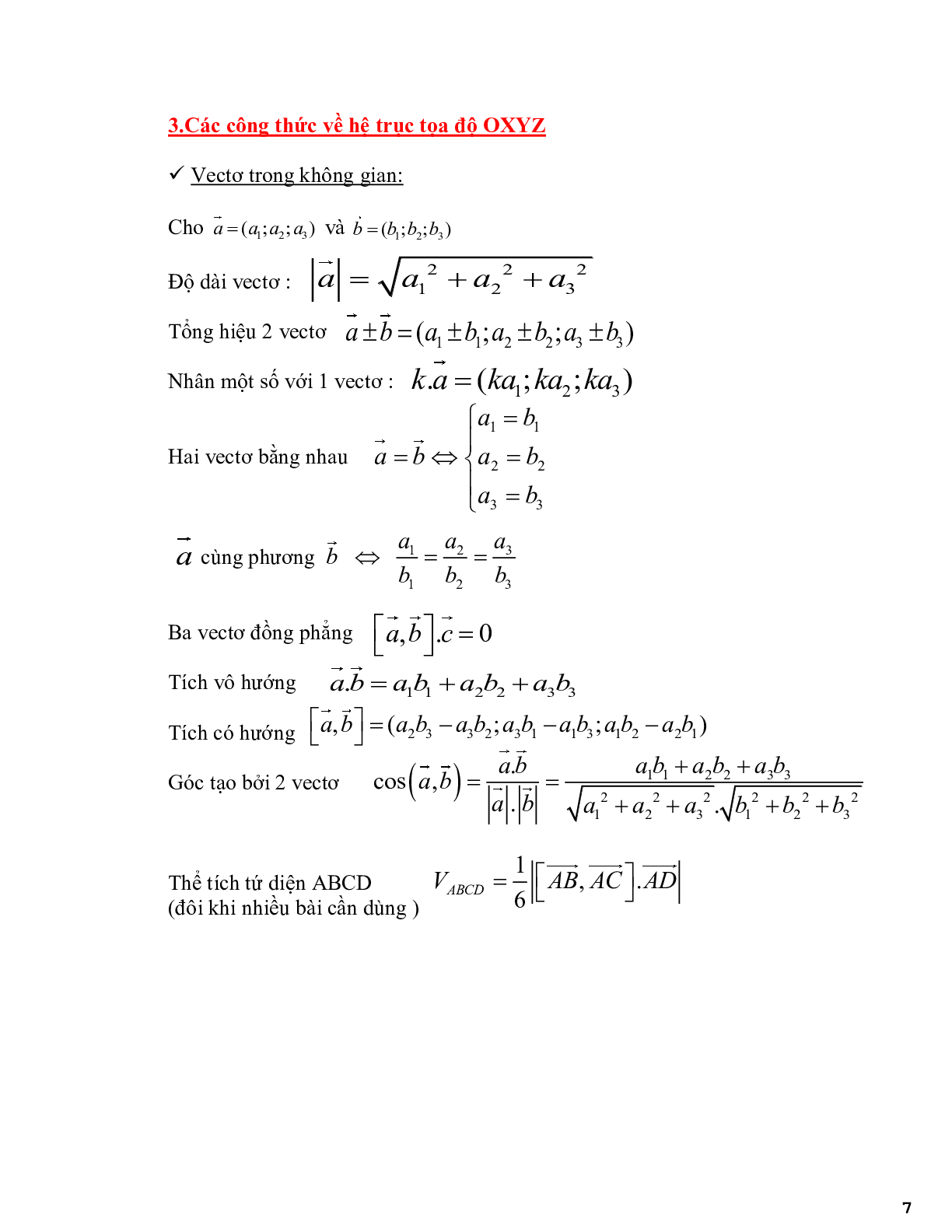Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Gắn hệ toạ độ Oxyz để giải các bài toán hình học không gian, tài liệu bao gồm 34 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Gắn hệ toạ độ Oxyz để giải các bài toán hình học không gian

Phần đầu tiên

Các kiến thức quan trọng (cần nhớ hết :v )

1.Các công thức về hình học

Diện tích các hình:

* Tam giác thường ( hoặc vuông như trong hình)

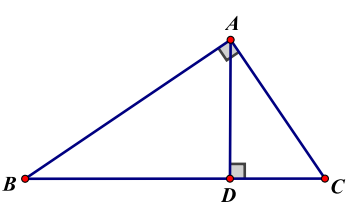
\( = \frac{1}{2}AC \cdot CB \cdot \sin C = \frac{{AB \cdot AC \cdot BC}}{{4R}} = pr\)

( với AD là đường cao, R là bán kính đường tròn ngoại tiếp, p là nửa chu vi, r là bán kính đường tròn nội tiếp )

* Mở rộng :

- Hệ thức lượng trong tam giác vuông ( như hình vẽ )

\(A{C^2} = CD \cdot CB\)

\(A{B^2} = BD.BC\)

\(B{C^2} = A{B^2} + A{C^2}\)

\(\frac{1}{{A{D^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow AD = \frac{{AB \cdot AC}}{{\sqrt {A{B^2} + A{C^2}} }}\)

\(A{D^2} = BD \cdot CD\)

\(AB \cdot AC = AD \cdot BC\)

- Hệ thức lượng trong mọi tam giác : (ví dụ tam giác thường như hình vẽ )

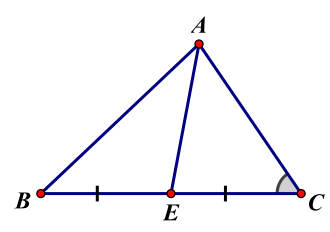
\(A{B^2} = B{C^2} + A{C^2} - 2BC \cdot AC \cdot \cos C\)

\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)

\(A{E^2} = \frac{1}{2}\left( {A{B^2} + A{C^2}} \right) - \frac{1}{4}B{C^2}\)

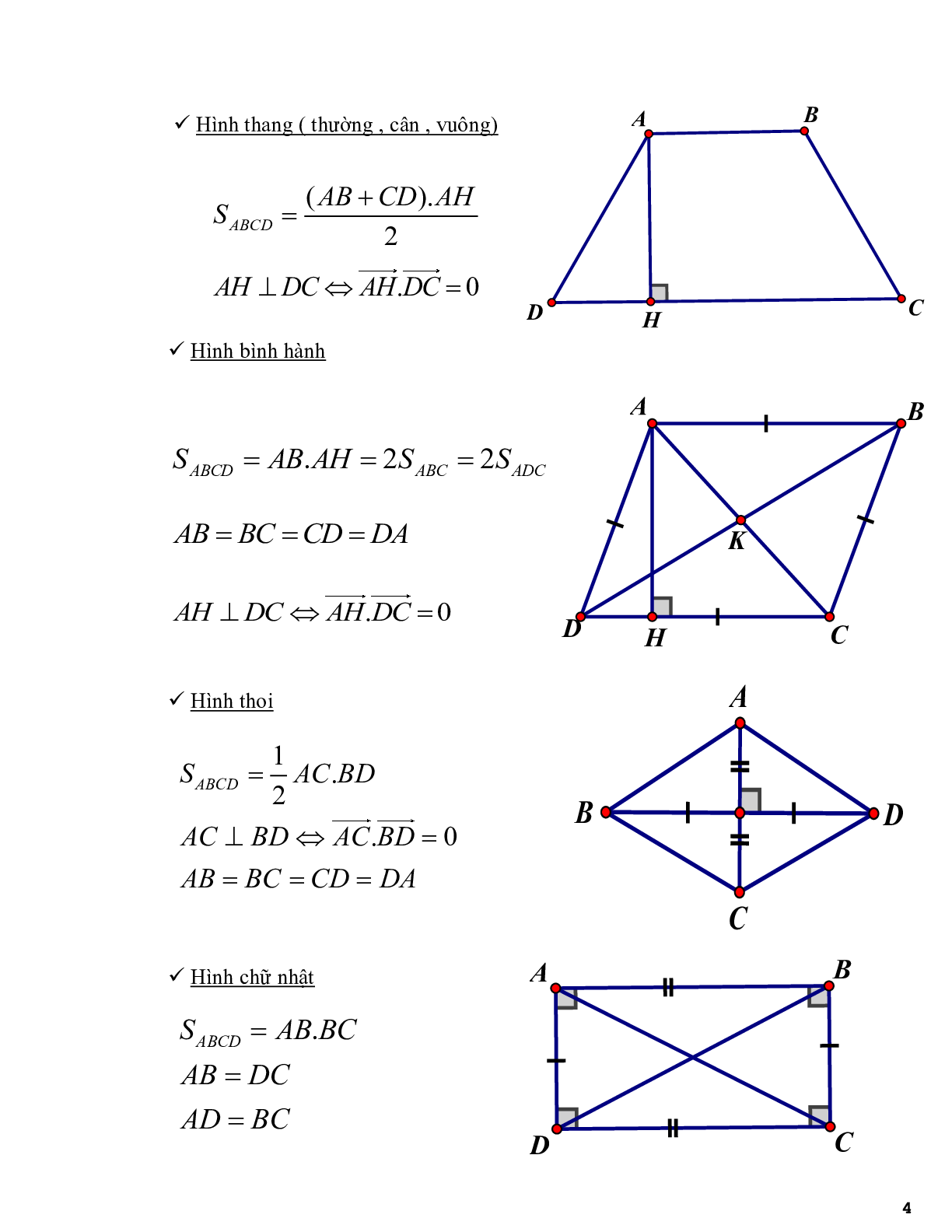
* Hình thang (thường, cân, vuông )

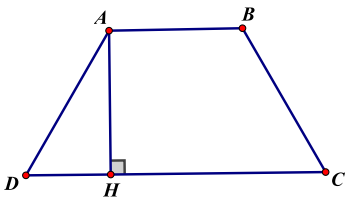
\({S_{ABCD}} = \frac{{(AB + CD) \cdot AH}}{2}\)

\(AH \bot DC \Leftrightarrow \overrightarrow {AH}  \cdot \overrightarrow {DC}  = 0\)

* Hình bình hành

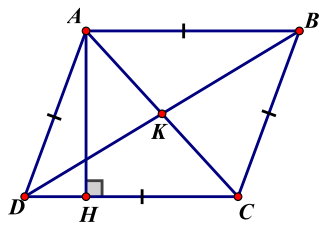
\({S_{ABCD}} = AB \cdot AH = 2{S_{ABC}} = 2{S_{ADC}}\)

\(AB = BC = CD = DA\)

\(AH \bot DC \Leftrightarrow \overrightarrow {AH}  \cdot \overrightarrow {DC}  = 0\)

* Hình thoi

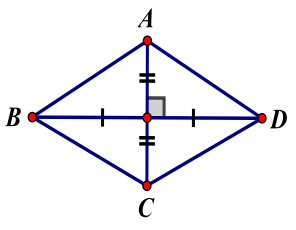
\({S_{ABCD}} = \frac{1}{2}AC \cdot BD\)

\(AC \bot BD \Leftrightarrow \overrightarrow {AC}  \cdot \overrightarrow {BD}  = 0\)

\(AB = BC = CD = DA\)

* Hình chữ nhật

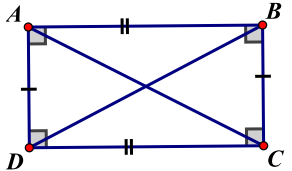
\({S_{ABCD}} = AB \cdot BC\)

\(AB = DC\)

\(AD = BC\)

* Hình vuông

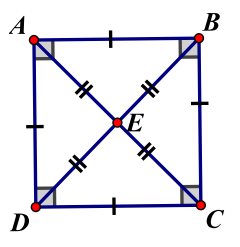
\({S_{ABCD}} = A{B^2} = B{C^2} = C{D^2} = A{D^2}\)

\(AB = BC = CD = DA\)

2.Các công thức tính thể tích các hình

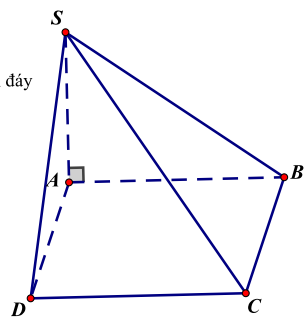
* Thể tích khối chóp

Cách tính: Lấy đường cao nhân diện tích đáy rồi chia 3

Ví dụ như hình vẽ thì: \({V_{SABC}} = \frac{1}{3}SA.{S_{ABCD}}\)

Chú ý :

- Hình chóp tam giác đều thì có đáy là tam giác đều và có các cạnh bên bằng nhau nhưng không bằng cạnh đáy (tức là các mặt bên là tam giác cân)

- Hình chóp đều thì có đáy là tam giác đều, các cạnh bên bằng nhau và bằng với cạnh đáy (các mặt bên cũng là tam giác đều).

- Còn hình chóp có đáy là tam giác đều và các cạnh bên không bằng nhau thì đề bài sẽ ghi là "Cho hình chóp có đáy là tam giác đều" và không nói gì thêm.

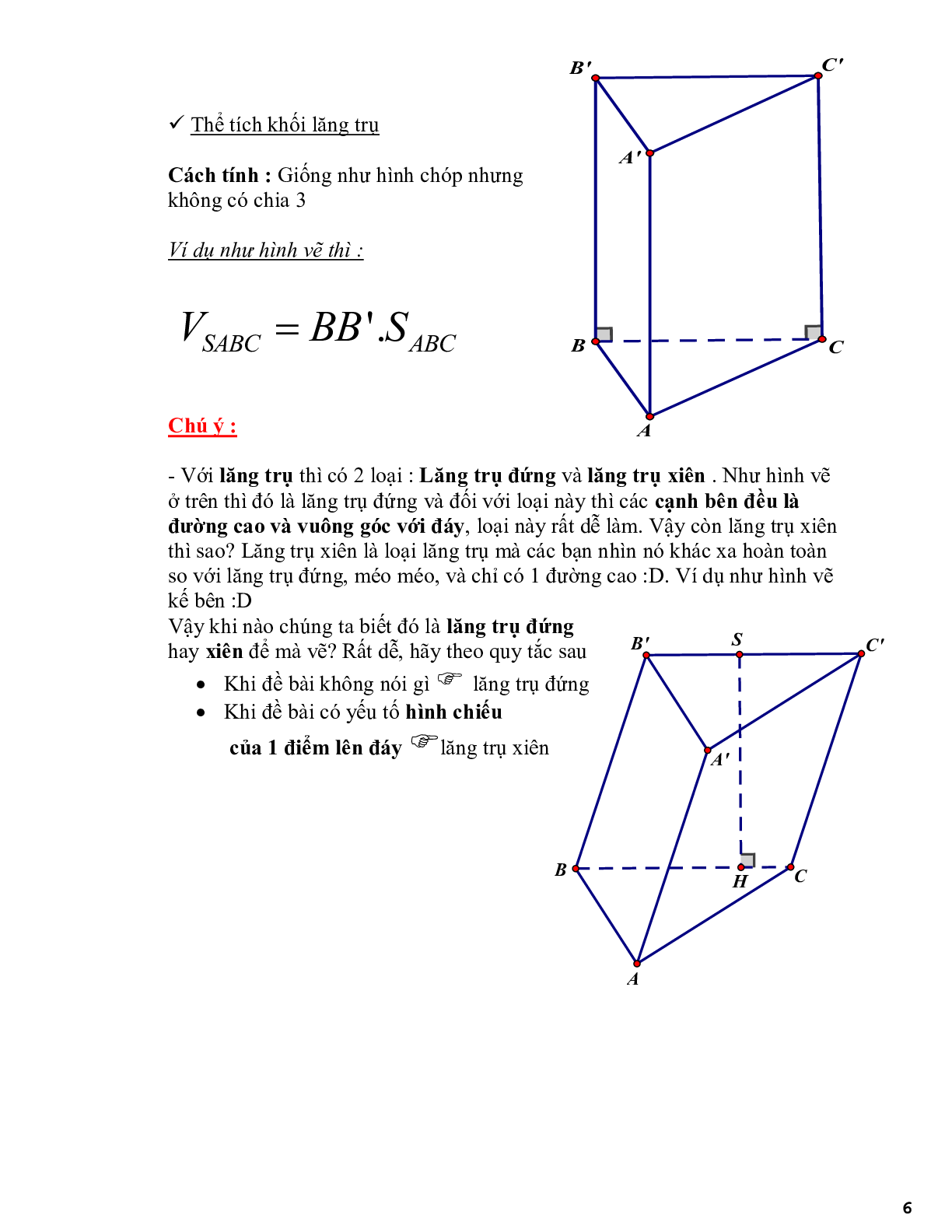
* Thể tích khối lăng trụ

Cách tính: giống như hình chóp nhưng k có chia 3

Ví dụ như hình vẽ thì:

\({V_{SABC}} = BB'.{S_{ABC}}\)

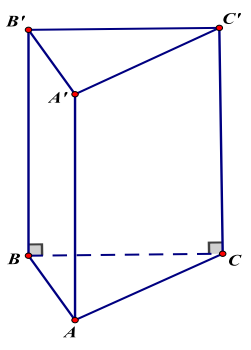
Chú ý :

- Với lăng trụ thì có 2 loại : Lăng trụ đứng và lăng trụ xiên . Như hình vẽ ở trên thì đó là lăng trụ đứng và đối với loại này thì các cạnh bên đều là đường cao và vuông góc với đáy, loại này rất dễ làm. Vậy còn lăng trụ xiên thì sao? Lăng trụ xiên là loại lăng trụ mà các bạn nhìn nó khác xa hoàn toàn so với lăng trụ đứng, méo méo, và chỉ có 1 đường cao :D Ví dụ như hình vẽ kế bên :D

Vậy khi nào chúng ta biết đó là lăng trụ đứng hay xiên để mà vẽ? Rất dễ, hãy theo quy tắc sau:

- Khi đề bài không nói gì lăng trụ đứng

- Khi đề bài có yếu tố hình chiếu của 1 điểm lên đáy lăng trụ xiên

3. Các công thức về hệ truc toa đô OXYZ

* Vecto trong không gian

Cho \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) và \(\vec b = \left( {{b_1};{b_2};{b_3}} \right)\)

Độ dài vectơ: \(|\vec a| = \sqrt {a_1^2 + a_2^2 + a_3^2} \)

Tổng hiệu 2 vectơ \(\quad \vec a \pm \vec b = \left( {{a_1} \pm {b_1};{a_2} \pm {b_2};{a_3} \pm {b_3}} \right)\)

Nhân một số với 1 vectơ: \(k \cdot \vec a = \left( {k{a_1};k{a_2};k{a_3}} \right)\)

Hai vectơ bằng nhau \(\quad \vec a = \vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_1} = {b_1}}\\{{a_2} = {b_2}}\\{{a_3} = {b_3}}\end{array}} \right.\)

\(\vec a\) cùng phương \(\vec b \Leftrightarrow \frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}}\)

Ba vectơ đồng phẳng \([\vec a,\vec b]\vec c = 0\)

Tích vô hướng \(\quad \vec a \cdot \vec b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\)

Tích có hướng \([\vec a,\vec b] = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\)

Góc tạo bởi 2 vectơ

\(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a| \cdot |\vec b|}} = \frac{{{a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}}}{{\sqrt {a_1^2 + a_2^2 + a_3^2}  \cdot \sqrt {b_1^2 + b_2^2 + b_3^2} }}\)

Thể tích tứ diện ABCD đôi khi nhiều bài cần dùng