Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 4 Bài 4: Bất phương trình bậc nhất một ẩn. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 4:Bất phương trình bậc nhất một ẩn. Mời các bạn đón xem:
Bài tập Toán 8 Chương 4 Bài 4: Bất phương trình bậc nhất một ẩn
A. Bài tập Bất phương trình bậc nhất một ẩn
I. Bài tập trắc nghiệm
Bài 1: Bất phương trình ax + b > 0 vô nghiệm khi
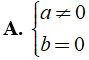
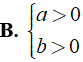
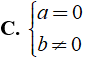
Nếu a > 0 thì ax + b > 0 ⇔ x > - nên
Nếu a < 0 thì ax + b > 0 ⇔ x < - nên
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.
Bài 2: Tập nghiệm S của bất phương trình: 5x - 1 ≥ + 3 là?
A. S = R
B. x > 2
C. x < -
D. x ≥ ;
Ta có: 5x - 1 ≥ + 3 ⇔ 25x - 5 ≥ 2x + 15 ⇔ 23x ≥ 20 ⇔ x ≥ .
Vậy tập nghiệm của bất phương trình là x ≥ ;
Chọn đáp án D.
Bài 3: Bất phương trình có bao nhiêu nghiệm nguyên lớn hơn - 10 ?
A. 4
B. 5
C. 9
D. 10
Ta có:
Vì x ∈ Z, - 10 < x ≤ - 5 nên có 5 nghiệm nguyên.
Chọn đáp án B.
Bài 4: Tập nghiệm S của bất phương trình: (1 - )x < là?
A. x > 2
B. x >
C. x < -
D. S = R
Vậy tập nghiệm của bất phương trình là: x >
Chọn đáp án B.
Bài 5: Bất phương trình ( 2x - 1 )( x + 3 ) - 3x + 1 ≤ ( x - 1 )( x + 3 ) + x2 - 5 có tập nghiệm là?
A. x < -
B. x ≥ -
C. S = R
D. S = Ø
Ta có: ( 2x - 1 )( x + 3 ) - 3x + 1 ≤ ( x - 1 )( x + 3 ) + x2 - 5
⇔ 2x2 + 5x - 3 - 3x + 1 ≤ x2 + 2x - 3 + x2 - 5 ⇔ 0x ≤ - 6
⇔ x ∈ Ø → S = Ø
Chọn đáp án D.
Bài 6: Giải bất phương trình : 2x + 4 < 16
A. x > 6
B. x < 6
C. x < 8
D. x > 8
Chọn đáp án B
Bài 7: Giải bất phương trình: 8x + 4 > 2(x+ 5)
A. x > 2
B. x < -1
C. x > -1
D. x > 1
Ta có: 8x + 4 > 2( x +5 )
⇔ 8x + 4 > 2x + 10
⇔ 8x – 2x > 10 - 4
⇔ 6x > 6
⇔ x > 6 : 6
⇔ x > 1
Chọn đáp án D
Bài 8: Giải bất phương trình:
Chọn đáp án C
Bài 9: Giải bất phương trình: (x + 2).(x – 3) > (2- x). (6 - x)
Chọn đáp án A
Bài 10: Tìm m để x = 2 là nghiệm bất phương trình: mx + 2 < x + 3 + m
A. m = 2
B. m < 3
C. m > 1
D. m < - 3
Do x = 2 là nghiệm của bất phương trình đã cho nên:
⇔ 2m + 2 < 2 + 3 + m
⇔ 2m – m < 2 + 3- 2
⇔ m < 3
Chọn đáp án B
II. Bài tập tự luận có giải
Bài 1: Bất phương trình 2(x + 2)2 < 2x(x + 2) + 4 có tập nghiệm là?
Lời giải
2(x + 2)2 < 2x(x + 2) + 4
⇔ 2x2 + 8x + 8 < 2x2 + 4x + 4
⇔ 4x < -4
⇔ x < -1.
Bài 2 Bất phương trình (x + 2)2 < x + x2 - 3 có nghiệm là?
Lời giải
Bài 3 Nghiệm của bất phương trình (x + 3)(x + 4) > (x - 2)(x + 9) + 25?
Lời giải
Ta có (x + 3)(x + 4) > (x - 2)(x + 9) + 25
⇔ x2 + 7x + 12 > x2 + 7x - 18 + 25
⇔ x2 + 7x + 12 - x2 - 7x + 18 - 25 > 0
⇔ 5 > 0
Vì 5 > 0 (luôn đúng) nên bất phương trình vô số nghiệm x R.
Bài 4 Nghiệm của bất phương trình (x + 3) (x + 4) > (x - 2)(x + 9) + 25 là?
Lời giải
Ta có: (x + 3)(x + 4) > (x - 2)(x + 9) + 25
⇔ x2 + 7x + 12 > x2 + 7x - 18 + 25
⇔ x2 + 7x + 12 - x2 - 7x + 18 - 25 > 0
⇔ 5 > 0
Vì 5 > 0 (luôn đúng) nên bất phương trình vô số nghiệm x R.
Bài 5 Tìm x để phân thức 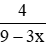
Lời giải
Phân thức 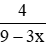
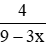
Vì 4 > 0 nên
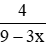
Vậy để phân thức 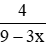
Bài 6 Trong các bất phương trình sau, hãy cho biết bất phương trình nào là bất phương trình bậc nhất một ẩn:
a) 2x – 3 < 0;
b) 0 . x + 5 > 0;
c) 5x – 15 ≥ 0;
d) x2 > 0.
Lời giải
Các bất phương trình a, b, c là các bất phương trình bậc nhất một ẩn
Bài 7 Giải các bất phương trình sau:
a) x + 12 > 21;
b) -2x > -3x – 5.
Lời giải
a) x + 12 > 21 ⇔ x > 21 - 12 ⇔ x > 9
Vậy tập nghiệm của bất phương trình x + 12 > 21 là {x|x > 9}
b) -2x > -3x – 5 ⇔ -2x + 3x > -5 ⇔ x > -5
Vậy tập nghiệm của bất phương trình -2x > -3x – 5 là {x|x > -5}
Bài 8 Giải các bất phương trình sau (dùng quy tắc nhân):
a) 2x < 24;
b) -3x < 27.
Lời giải
a) 2x < 24 ⇔ 2x. < 24.
⇔ x < 12
Vậy tập nghiệm của bất phương trình 2x < 24 là {x|x < 12}
b) -3x < 27 ⇔ -3x. > 27.
⇔ x > -9
Vậy tập nghiệm của bất phương trình - 3x < 27 là {x|x > -9}
Bài 9 Giải thích sự tương đương:
a) x + 3 < 7 ⇔ x – 2 < 2;
b) 2x < - 4 ⇔ -3x > 6.
Lời giải
a) x + 3 < 7 ⇔ x + 3 - 5 < 7-5 ⇔ x – 2 < 2
b) 2x < -4 ⇔ 2x. > -4.
⇔ -3x > 6
Bài 10 Giải bất phương trình - 4x – 8 < 0 và biểu diễn tập nghiệm trên trục số.
Lời giải
- 4x – 8 < 0 ⇔ -4x < 8 ⇔ x > -2
Vậy tập nghiệm của bất phương trình -4x – 8 < 0 là {x|x > -2}
Biểu diễn trên trục số
Bài 11 Giải bất phương trình -0,2x – 0,2 > 0,4x – 2.
Lời giải
- 0,2x – 0,2 > 0,4x – 2
⇔ 0,4x – 2 < -0,2x – 0,2
⇔ 0,4x + 0,2x < -0,2 + 2
⇔ 0,6x < 1,8
⇔ x < 3
Vậy tập nghiệm của bất phương trình -0,2x – 0,2 > 0,4x – 2 là {x|x < 3}
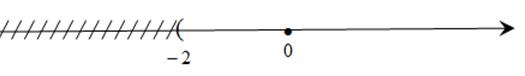
III. Bài tập vận dụng
Bài 1 Giải các bất phương trình (theo quy tắc chuyển vế):
a) x - 5 > 3
b) x - 2x < -2x + 4
c) -3x > -4x + 2
d) 8x + 2 < 7x - 1
Bài 2 Giải các bất phương trình (theo quy tắc nhân):
a) 0,3x > 0,6 ; b) -4x < 12
c) -x > 4 ; d) 1,5x > -9
Bài 3 Giải thích sự tương đương sau:
a) x - 3 > 1 ⇔ x + 3 > 7
b) -x < 2 ⇔ 3x > -6
Bài 4 Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 1,2x < -6 ; b) 3x + 4 > 2x + 3
Bài 5 Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 2x - 3 > 0; b) 3x + 4 < 0
c) 4 - 3x ≤ 0; d) 5 - 2x ≥ 0
Bài 6 Giải các bất phương trình:
a) 2x - 1 > 5; b) 3x - 2 < 4
c) 2 - 5x ≤ 17; d) 3 - 4x ≥ 19
Bài 7 Giải các bất phương trình:
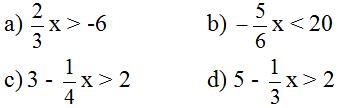
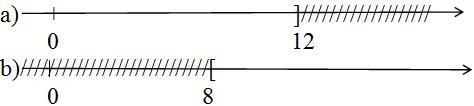
Bài 8 Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (Kể ba bất phương trình có cùng tập nghiệm).
Bài 9 Đố: Kiểm tra xem giá trị x = -2 có là nghiệm của bất phương trình sau không?
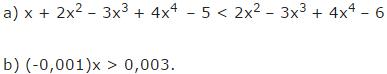
Bài 10 Cho bất phương trình x2 > 0.
a) Chứng tỏ x = 2, x = -3 là nghiệm của bất phương trình đã cho.
b) Có phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho hay không?
B. Lý thuyết Bất phương trình bậc nhất một ẩn
Bất phương trình bậc nhất một ẩn là bất phương trình có dạng (hoặc ) trong đó a, b là hai số đã cho và .
* Các quy tắc
- Quy tắc chuyển vế; Khi chuyển một hạng tử từ một vế của bất phương trình sang vế còn lại, ta phải đổi dấu hạng tử đó.
Ví dụ
- Quy tắc nhân (hoặc chia) với một số khác 0: Khi nhân (hoặc chia) hai vế của bất phương trình với một số khác 0 ta phải giữ nguyên chiều bất phương trình (nếu số đó dương) hoặc đổi chiều bất phương trình (nếu số đó âm) ta được bất phương trình mới tương đương với bất phương trình đã cho.
Ví dụ:
với .
với .
với .
với .
* Cách giải bất phương trình bậc nhất 1 ẩn
Ta có:
(sử dụng quy tắc chuyển vế)
(sử dụng quy tắc chia cho một số dương)
* Tương tự cho các trường hợp còn lại (chú ý tuân thủ hai quy tắc ở trên)