Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 7 sách Kết nối tri thức năm 2025 – 2026. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THCS dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 1 Toán 7. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 7 Kết nối tri thức bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Bộ 10 đề thi học kì 1 Toán lớp 7 Kết nối tri thức có đáp án - Đề 1
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Kết nối tri thức
Năm học ................
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 1)
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Kết quả của phép tính: là:
A. B. C. D.
Câu 2: Số nào dưới đây là số vô tỉ?
A. B. C. D.
Câu 3: Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thể giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 . (Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
A. B. C. D.
Câu 4: Kết quả của phép tính: là:
A. B. C. D.
Câu 5: Tính số đo của góc trong hình vẽ dưới đây:
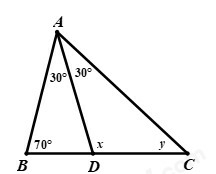
A. B. C. D.
Câu 6: Quan sát hình vẽ sau:
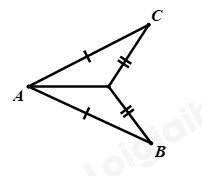
Tính số đo của góc , biết .
A. B. C. D.
Câu 7: Cho tam giác và tam giác có . Cần thêm một điều kiện gì để tam giác và tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông?
A. B. C. D.
Câu 8: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:
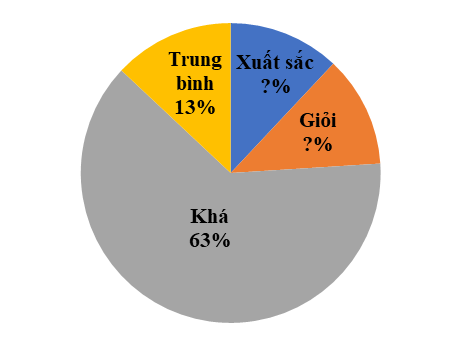
Tìm tỉ số phần trăm số học sinh xuất sắc và số hóc inh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi.
A. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
B. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
C. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
D. Số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) b)
c) d)
Bài 2: (2,0 điểm)
Tìm , biết:
a) b)
c) d)
Bài 3: (1,0 điểm) Trong hình vẽ bên dưới có . Biết
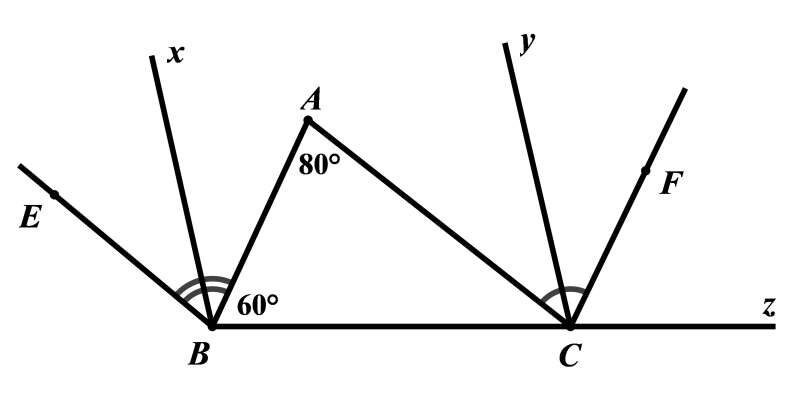
a) Chứng minh rằng ;
b) Tính số đo của các góc và .
c) Gọi lần lượt là tia phân giác của các góc và . Chứng minh rằng .
Bài 4: (1,5 điểm) Cho tam giác nhọn, lấy điểm là trung điểm của cạnh , lấy điểm là trung điểm của cạnh . Trên tia đối của tia lấy điểm sao cho . Chứng minh rằng:
a) Hai tam giác bằng nhau;
b) song song với ;
c) .
Bài 5: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức:
Hướng dẫn giải:
Phần I: Trắc nghiệm
|
1.B |
2.A |
3.C |
4.A |
5.C |
6.A |
7.C |
8.D |
Câu 1
Phương pháp:
Sử dụng quy ước: với
Thực hiện phép cộng với số hữu tỉ.
Cách giải:
Chọn B.
Câu 2
Phương pháp:
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Cách giải:
Ta có: là số thập phân vô hạn tuần hoàn
không phải là số vô tỉ
là số hữu tỉ.
Do đó, là số vô tỉ.
Chọn A.
Câu 3
Phương pháp:
Gọi độ dài cạnh hình vuông là
Tính căn bậc hai số học của là độ dài cạnh đáy của kim tự tháp cần tìm.
Cách giải:
Gọi độ dài cạnh hình vuông là
Theo giả thiết, ta có:
Vậy độ dài cạnh đáy của kim tự tháp xấp xỉ 228,5m.
Chọn C.
Câu 4
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực:
Cách giải:
Ta có:
Vì nên do đó,
Suy ra
Do đó,
Ta có:
Chọn A.
Câu 5
Phương pháp:
Áp dụng định lý góc ngoài của tam giác: góc ngoài của tam giác bằng tổng hai góc trong không kề với nó, tính số đo của .
Áp dụng định lý tổng ba góc trong một tam giác, tính số đo của
Cách giải:
*Tam giác có là góc ngoài tại đỉnh , ta có:
(góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
*Xét tam giác có: (định lý tổng ba góc trong một tam giác)
Vậy
Chọn C.
Câu 6
Phương pháp:
Vận dụng định lí: Nếu ba cạnh của tam giác bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Cách giải:
Xét và có:
(giả thiết)
(giả thiết)
là cạnh chung
Suy ra
Do đó, (hai góc tương ứng)
Mà nên
Chọn A.
Câu 7
Phương pháp:
Áp dụng định lý: Nếu cạnh huyền và một cạnh góc vuông của tam giác này bằng cạnh huyền và một cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Cách giải:
Hai tam giác và có mà lầm lượt là hai cạnh góc vuông của hai tam giác và nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là .
Chọn C.
Câu 8
Phương pháp:
Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn.
Cách giải:
Gọi số phần trăm học sinh xuất sắc là (điều kiện: ). Vì số học sinh xuất sắc bằng số học sinh giỏi nên số phần trăm học sinh giỏi là (điều kiện: ).
Ta có:
Vậy số học sinh xuất sắc chiếm , số học sinh giỏi chiếm .
Chọn D.
Phần II. Tự luận:
Bài 1
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ.
b) Tính căn bậc hai của một số.
Lũy thừa của một số hữu tỉ: .
Thực hiện các phép toán với số hữu tỉ.
c) Thực hiện tính căn bậc hai của một số.
d) Vận dụng kiến thức giá trị tuyệt đối của một số thực:
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a)
b)
c)
d)
Bài 2
Phương pháp:
a) Giải:
Trường hợp 1: Giải
Trường hợp 2: Giải
b) Giải
Trường hợp 1:
Trường hợp 2:
c) Giải:
Trường hợp 1: Giải
Trường hợp 2: Giải
Vận dụng kiến thức giá trị tuyệt đối của một số thực:
d) vận dụng kiến thức giá trị tuyệt đối của một số thực:
Cách giải:
|
a) Trường hợp 1:
Vì với mọi nên với mọi Do đó, với mọi Vậy không có thỏa mãn . Trường hợp 2:
Vậy
|
b)
|
|||||
|
Trường hợp 1:
Vậy
|
Trường hợp 2:
|
|||||
|
c)
Vậy |
d)
Vậy |
|||||
Bài 3
Phương pháp:
a) Vận dụng tính chất của hai đường thẳng song song.
b) Hai góc kề bù có tổng số đo bằng .
Vận dụng định lý tổng ba góc trong một tam giác.
c) Vận dụng dấu hiệu nhận biết của hai đường thẳng song song.
Cách giải:
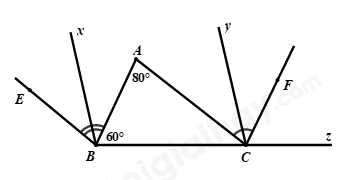
a) Vì (giả thiết) nên (hai góc so le trong)
Vì (giả thiết) nên (hai góc so le trong)
Suy ra (vì cùng bằng )
b) Vì (giả thiết) nên (hai góc đồng vị)
Ta có và là hai góc kề bù nên
Xét tam giác có: (định lí tổng ba góc trong một tam giác)
Vậy .
c) Ta có:
là tia phân giác của (giả thiết) suy ra (tính chất tia phân giác của một góc)
là tia phân giác của (giả thiết) suy ra (tính chất tia phân giác của một góc)
Ta có:
và là hai góc kề nhau nên
và là hai góc kề nhau nên
Vì mà hai góc này ở vị trí đồng vị nên (dấu hiệu nhận biết hai đường thẳng song song).
Bài 4
Phương pháp:
a) Vận dụng định lý: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau theo trường hợp cạnh – góc – cạnh (c.g.c).
b) Vận dụng dấu hiệu nhận biết của hai đường thẳng song song.
c) Vận dụng định lý: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau theo trường hợp cạnh – góc – cạnh (c.g.c).
Vận dụng tính chất trung điểm của đoạn thẳng, tính chất bắc cầu.
Cách giải:
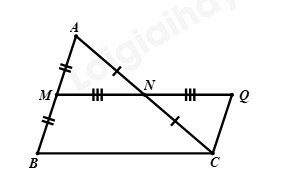
a) Vì là trung điểm của nên
Xét và có:
(chứng minh trên)
(hai góc đối đỉnh)
(giả thiết)
Suy ra
b) Vì (chứng minh a), suy ra (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên
Suy ra (điều phải chứng minh)
c) Vì (chứng minh a), suy ra (hai cạnh tương ứng)
Lại có, là trung điểm của nên
Suy ra, (vì cùng bằng )
Vì (chứng minh b) nên (hai góc so le trong)
Xét và có:
(chứng minh trên)
(chứng minh trên)
là cạnh chung
Suy ra (hai cạnh tương ứng)
Vì . Do đó, (điều phải chứng minh)
Bài 5
Phương pháp:
Vận dụng kiến thức lũy thừa của một số và căn bậc hai số học của một số.
Cách giải:
Ta có:
Dấu “=” xảy ra khi và chỉ khi .
Vậy giá trị nhỏ nhất của là khi
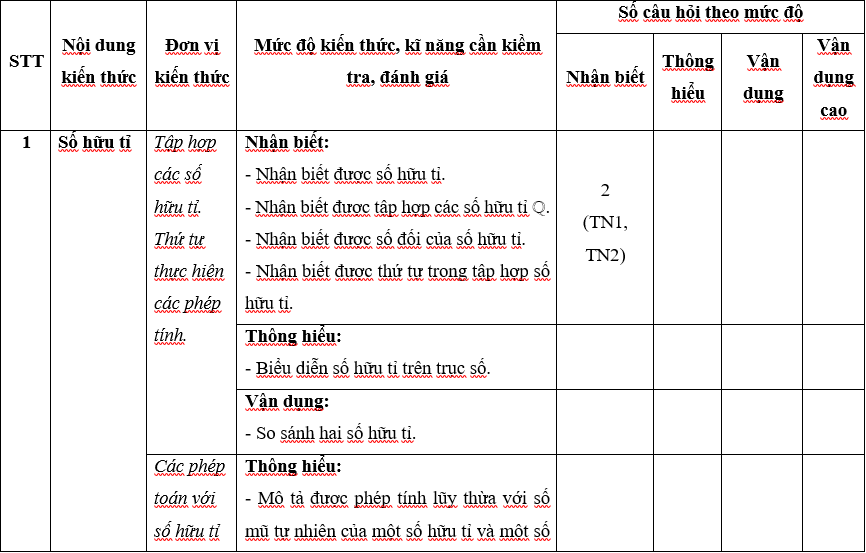
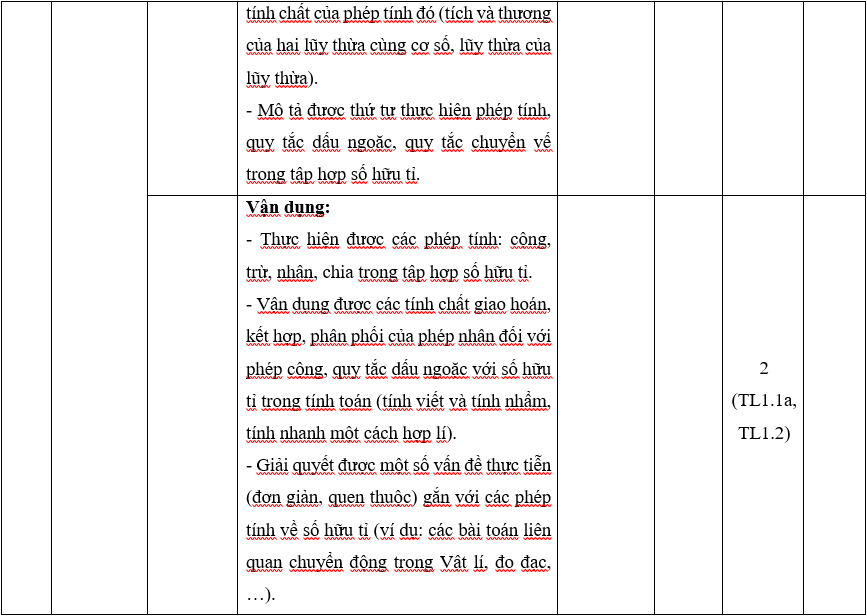
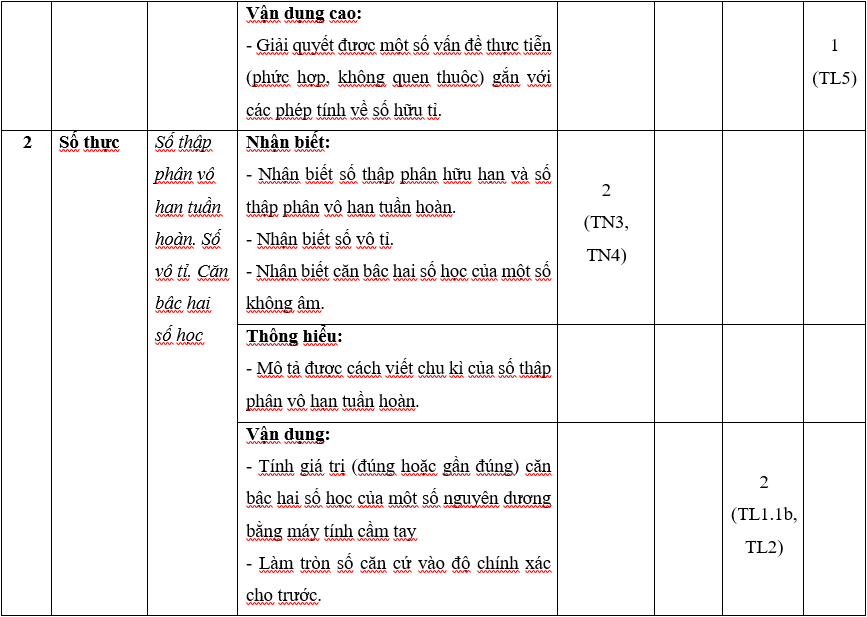
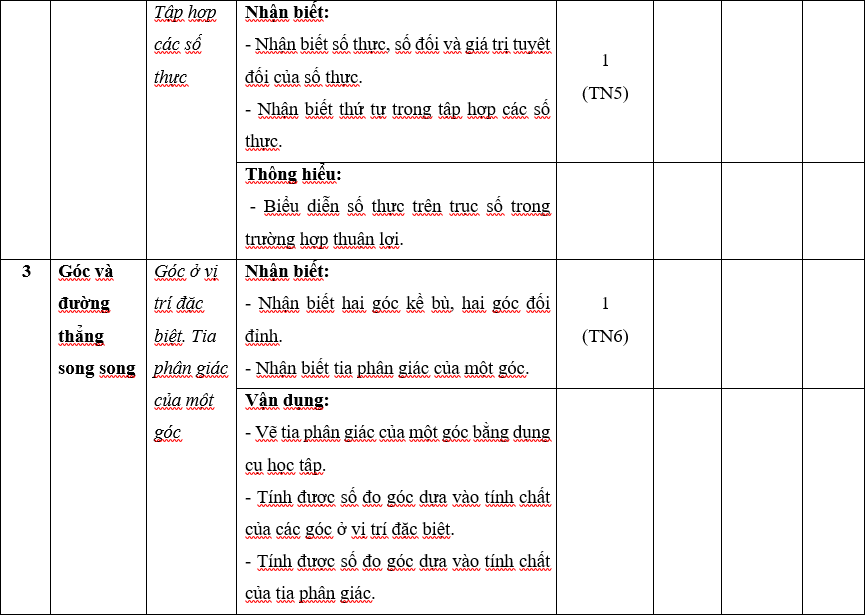
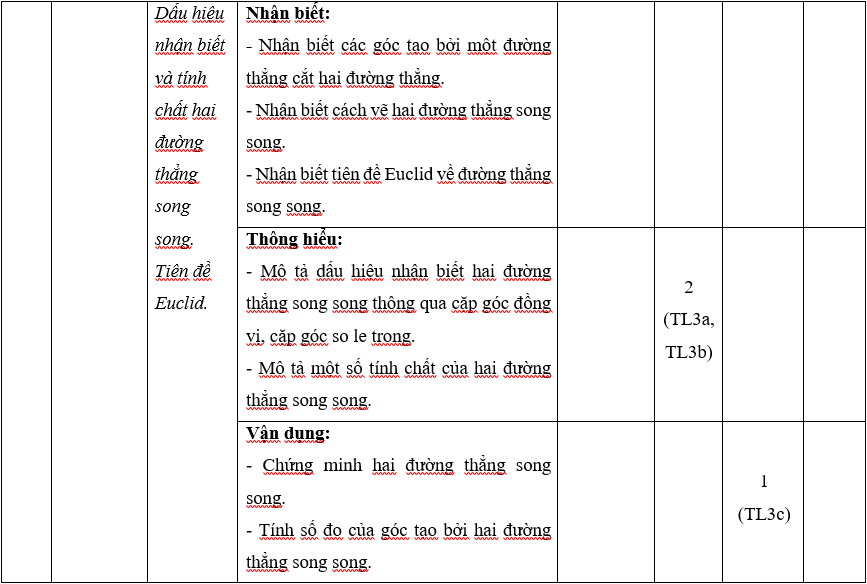
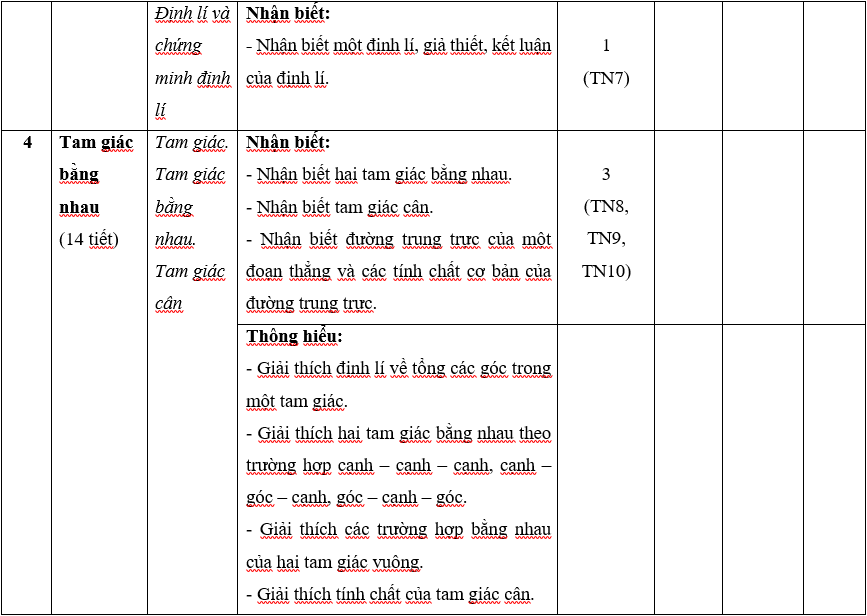
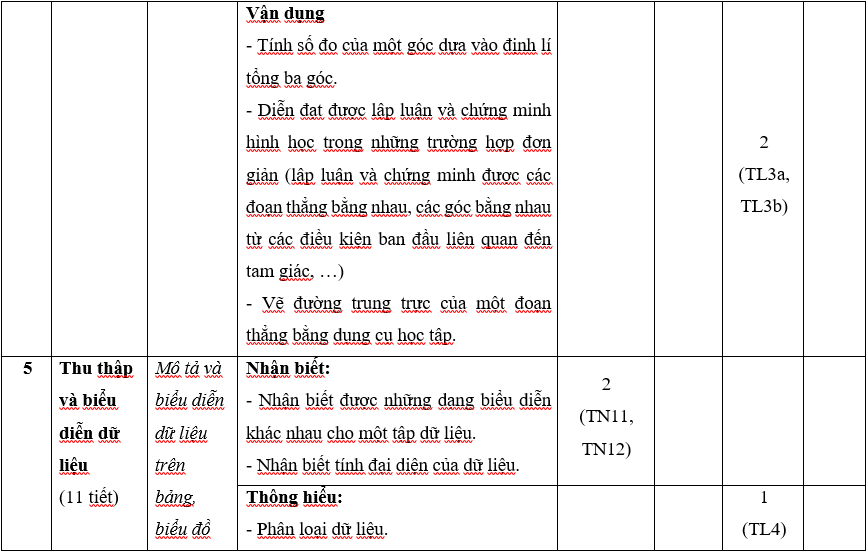
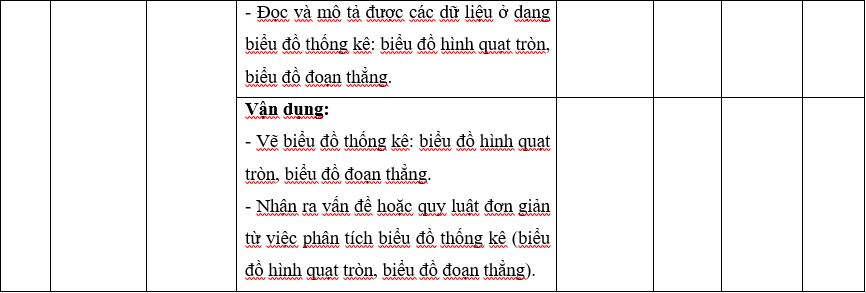
Ma trận 1 đề thi Học kì 1 môn Toán lớp 7 (Kết nối tri thức)
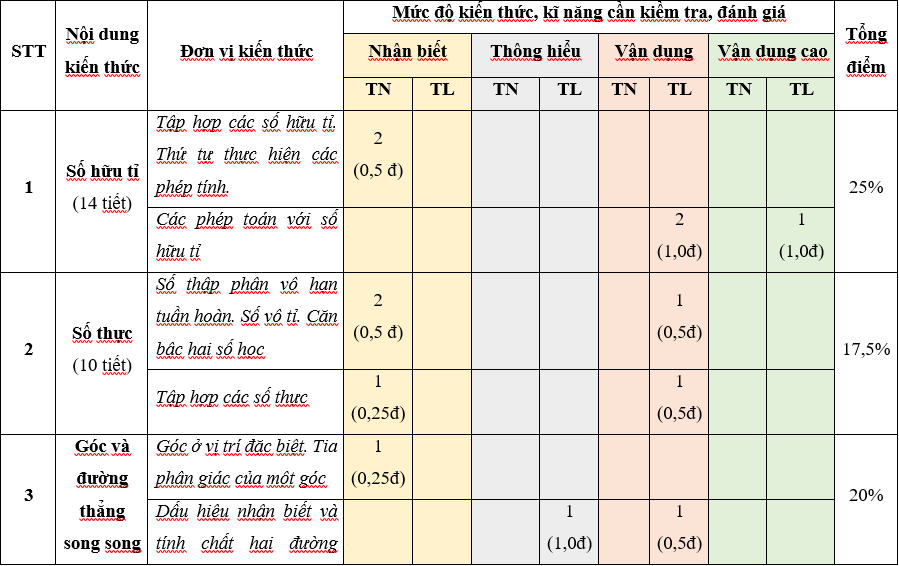
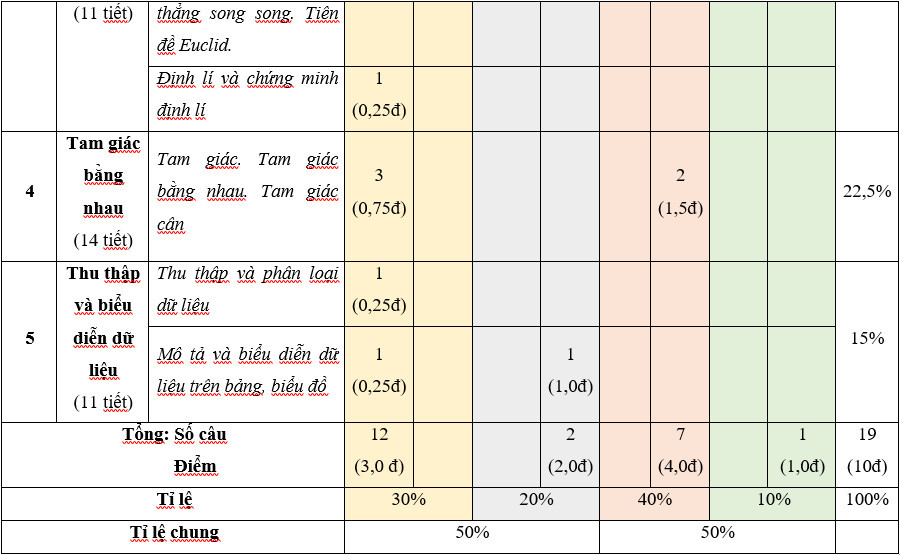
A.1. Bảng đặc ma trận 1 đề thi Học kì 1 môn Toán lớp 7 (Kết nối tri thức)
Bộ 10 đề thi học kì 1 Toán lớp 7 Kết nối tri thức có đáp án - Đề 2
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Kết nối tri thức
Năm học ................
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 2)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Số nào dưới đây đang biểu diễn số hữu tỉ?
A. ;
B. ;
C. ;
D. .
Câu 2. Trong các số sau, số nào biểu diễn số đối của số hữu tỉ –0,5?
A. ;
B. ;
C. 2;
D. –2.
Câu 3. Số là số:
A. Số thập phân vô hạn không tuần hoàn;
B. Số thập phân hữu hạn;
C. Số thập phân vô hạn tuần hoàn;
D. Số vô tỉ.
Câu 4. bằng:
A. ± 8;
B. –8;
C. 8;
D. 64.
Câu 5. Nếu |x| = 2 thì:
A. x = 2;
B. x = –2;
C. x = 2 hoặc x = –2;
D. Không có giá trị nào của x thỏa mãn.
Câu 6. Quan sát hình vẽ.
Có tất cả bao nhiêu góc kề bù với ?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 7. Trong các câu sau, câu nào không phải định lí?
A. Nếu hai góc bằng nhau thì chúng đối đỉnh;
B. Nếu hai góc kề bù thì tổng số đo của chúng bằng 180°;
C. Nếu hai góc bù nhau thì tổng số đo của chúng bằng 180°;
D. Nếu hai góc đối đỉnh thì chúng bằng nhau.
Câu 8. Tổng số đo ba góc của một tam giác là
A. 45°;
B. 60°;
C. 90°;
D. 180°.
Câu 9. Phát biểu nào dưới đây là sai?
A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau;
B. Hai tam giác bằng nhau thì có các góc tương ứng bằng nhau;
C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau thì hai tam giác đó bằng nhau.
D. Hai tam giác bằng nhau là hai tam giác có các cạnh bằng nhau và có các góc bằng nhau.
Câu 10. Cho các hình vẽ sau:
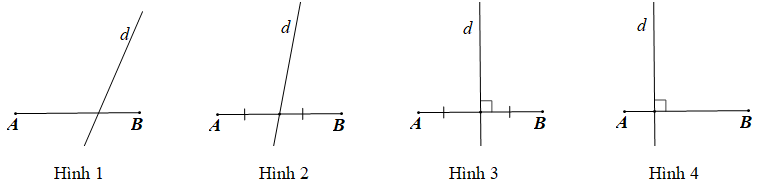
Hình vẽ nào minh họa đường thẳng d là đường trung trực của đoạn thẳng AB?
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 11. Thân nhiệt (°C) của bạn An trong cùng khung giờ 7h sáng các ngày trong tuần được ghi lại trong bảng sau:
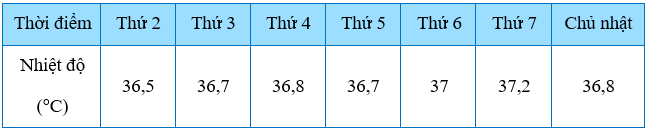
Bạn An đã thu được dữ liệu trên bằng cách nào?
A. Xem tivi;
B. Lập bảng hỏi;
C. Ghi chép số liệu thống kê hằng ngày;
D. Thu thập từ các nguồn có sẵn như: sách, báo, web.
Câu 12. Kết quả tìm hiểu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C cho bởi bảng thống kê sau:

Kết quả tìm hiểu về khả năng chơi bóng đá của các bạn học sinh nữ của lớp 7C được cho bởi bảng thống kê sau:

Khẳng định nào dưới đây là đúng?
A. Dữ liệu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;
B. Dữ liệu về khả năng chơi bóng đá của các bạn học sinh nữ lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;
C. Dữ liệu về khả năng chơi cầu lông và bóng đá được thống kê chưa đủ đại diện cho khả năng chơi thể thao của các bạn lớp 7C;
D. Lớp 7C có 35 học sinh.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
1. Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
a)
b)
2. Tìm x, biết: 2x – 3 – 3.2x = – 92.
Bài 2. (0,5 điểm) Kết quả điểm môn Toán của Mai trong học kỳ 1 như sau:
Điểm đánh giá thường xuyên: 7; 8; 8; 9;
Điểm đánh giá giữa kì: 8;
Điểm đánh giá cuối kì: 10.
Hãy tính điểm trung bình môn Toán của Mai và làm tròn với độ chính xác 0,05.
Bài 3. (3,0 điểm) Cho tam giác ABC, lấy M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
a) Chứng minh DAMB = DDMC;
b) Chứng minh AC // BD;
c) Kẻ AH ⊥ BC, DK ⊥ BC (H, K thuộc BC). Chứng minh BK = CH;
d) Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của DE.
Bài 4. (1,0 điểm) Cho biểu đồ sau:
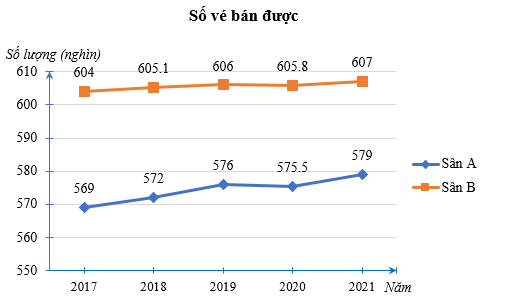 a) Trục đứng ở biểu đồ trên biểu diễn đại lượng gì? Dữ liệu về đại lượng này thuộc loại nào?
a) Trục đứng ở biểu đồ trên biểu diễn đại lượng gì? Dữ liệu về đại lượng này thuộc loại nào?
b) Lập bảng thống kê cho dữ liệu được biểu diễn trên biểu đồ.
c) Sân nào được bán nhiều vé hơn? Giải thích.
Bài 5. (1,0 điểm) Một cửa hàng bán trái cây nhập về số cam với giá 15 000 đồng/kg và niêm yết giá bán 22 000 đồng/kg. Quản lí cửa hàng đưa ra ba phương án kinh doanh (tính trên mỗi lô hàng trái cây là 20 kg) như sau:
Phương án 1: Cửa hàng bán 8 kg cam đầu tiên với giá niêm yết 22 000 đồng/kg và 12 kg còn lại với giá giảm 15% so với giá niêm yết.
Phương án 2: Cửa hàng bán 5 kg cam đầu tiên với giá giảm 7% so với giá niêm yết, bán 9 kg cam tiếp theo với giá giảm 10% so với giá niêm yết và bán 6 kg cam cuối cùng với giá giảm 15% so với giá niêm yết.
Phương án 3: Cửa hàng bán cả 20 kg cam với giá giảm 10% so với giá niêm yết.
Theo em, cửa hàng nên chọn phương án nào để có lãi nhất? Biết rằng chi phí vận hành không đáng kể.
Đáp án đề thi Học kì 1 môn Toán lớp 7 Kết nối tri thức - (Đề số 2)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
A |
A |
C |
C |
B |
B |
A |
D |
A |
C |
C |
C |
Hướng dẫn giải phần trắc nghiệm
Câu 1.
Đáp án đúng là: A
Số hữu tỉ là số viết được dưới dạng phân số , với a, b ∈ ℤ; b ≠ 0.
Do đó ta sẽ đi tìm phân số có tử số, mẫu số đều là số nguyên và mẫu số khác 0.
Trong tất cả các phương án chỉ có phân số thỏa mãn điều kiện trên nên là số biểu diễn số hữu tỉ.
Vậy ta chọn phương án A.
Câu 2.
Đáp án đúng là: A
Ta có
Vậy số đối của số hữu tỉ –0,5 là .
Ta chọn phương án A.
Câu 3.
Đáp án đúng là: C
Ta có:
Số –0,(3) là số thập phân vô hạn tuần hoàn chu kì 3.
Do đó số là số thập phân vô hạn tuần hoàn.
Ta chọn phương án C.
Câu 4.
Đáp án đúng là: C
Ta có .
Vậy ta chọn phương án C.
Câu 5.
Đáp án đúng là: B
Ta có |x| = 2
Suy ra x = 2 hoặc x = –2.
Vậy ta chọn phương án B.
Câu 6.
Đáp án đúng là: B
Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.
Do đó các góc kề bù với là
Vậy có tất cả 2 góc kề bù với .
Ta chọn phương án B.
Câu 7.
Đáp án đúng là: A
Hai góc bù nhau là hai góc có tổng số đo bằng 180° nên C đúng.
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau mà hai góc bù nhau là hai góc có tổng số đo bằng 180° nên B đúng.
Hai góc đối đỉnh thì bằng nhau nên D đúng.
Hai góc bằng nhau chưa chắc đã đối đỉnh nên khẳng định này sai.
Chẳng hạn:
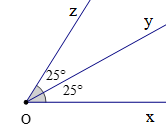
Ví dụ: (cùng bằng 25°) nhưng là hai góc kề nhau, không phải là hai góc đối đỉnh.
Do đó phương án A không phải là một định lí nên A sai.
Vậy ta chọn phương án A.
Câu 8.
Đáp án đúng là: D
Theo định lí: Tổng số đo ba góc của một tam giác bằng 180°.
Vậy ta chọn phương án D.
Câu 9.
Đáp án đúng là: A
Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau thì hai tam giác đó bằng nhau. Ngược lại, hai tam giác bằng nhau thì có các cạnh tương ứng bằng nhau và có các góc tương ứng bằng nhau.
Do đó phương án A là sai, hai tam giác có các góc tương ứng bằng nhau chưa chắc là hai tam giác bằng nhau.
Vậy ta chọn phương án A.
Câu 10.
Đáp án đúng là: C
Đường thẳng d là đường trung trực của đoạn thẳng AB nếu đường thẳng d vuông góc với AB tại trung điểm của AB.
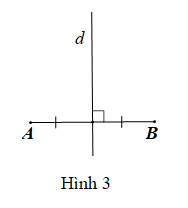
Vậy ta chọn phương án C.
Câu 11.
Đáp án đúng là: C
Bạn An đo thân nhiệt cơ thể mình lúc 7h sáng bằng nhiệt kế, sau đó ghi chép số liệu thống kê theo từng ngày.
Vậy ta chọn phương án C.
Câu 12.
Đáp án đúng là C
Dữ liệu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C chưa đủ đại diện cho học sinh cả lớp 7C vì chưa thống kê khả năng chơi cầu lông của các bạn nữ. Do đó A sai.
Dữ liệu về khả năng chơi bóng đá của các bạn học sinh nữ lớp 7C chưa đủ đại diện cho học sinh cả lớp 7C vì chưa thống kê khả năng chơi bóng đá của các bạn nam. Do đó B sai.
Dữ liệu về khả năng chơi cầu lông và bóng đá được thống kê chưa đủ đại diện cho khả năng chơi cầu lông và bóng đá nên cũng không thể đại diện cho khả năng chơi thể thao của các bạn lớp 7C. Do đó C đúng.
Tổng số học sinh lớp 7C là: 2 + 15 + 3 + 15 + 3 = 38 (bạn). Do đó phương án D sai.
Vậy ta chọn phương án C.
PHẦN II. TỰ LUẬN (7,0 điểm)
Hướng dẫn giải phần tự luận
Bài 1.
1.1.
a)
b)
1.2.
2x – 3 – 3.2x = – 92
Suy ra x = 5.
Vậy x = 5.
Bài 2.
Ta biết rằng điểm môn Toán được tính theo ba hệ số khác nhau.
Điểm đánh giá thường xuyên sẽ là hệ số 1; điểm đánh giá giữa kì sẽ là hệ số 2; điểm đánh giá cuối kì sẽ là hệ số 3.
Điểm trung bình môn Toán của Mai là:
(điểm)
Để làm tròn điểm trung bình môn Toán của Mai với độ chính xác 0,05 thì ta làm tròn kết quả trên đến hàng phần mười, khi đó ta được số 8,7.
Vậy điểm trung bình môn Toán của Mai với độ chính xác 0,05 là 8,7.
Bài 3.
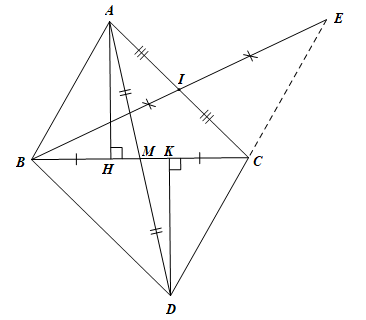
a) Xét DAMB và DDMC có:
MA = MD (giả thiết);
(hai góc đối đỉnh);
MB = MC (do M là trung điểm của BC).
Vậy DAMB = DDMC (c.g.c).
b) Xét DAMC và DDMB có:
MA = MD (giả thiết);
(hai góc đối đỉnh);
MB = MC (do M là trung điểm của BC).
Do đó DAMC = DDMB (c.g.c).
Suy ra (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên AC // BD.
c) Vì DAMB = DDMC (chứng minh câu a)
Nên AB = CD (hai cạnh tương ứng) và (hai góc tương ứng)
Xét DAHB và DDKC có:
AB = CD (chứng minh trên);
(do ).
Do đó DABH = DDKC (cạnh huyền – góc nhọn).
Suy ra BH = CK (hai cạnh tương ứng).
Khi đó BH + HK = CK + HK hay BK = CH.
d) Xét DAIB và DCIE có:
IA = IC (do I là trung điểm của AC);
(hai góc đối đỉnh);
IB = IE (do I là trung điểm của BE).
Do đó DAIB = DCIE (c.g.c).
Suy ra (hai góc tương ứng) và AB = CE hai cạnh tương ứng).
Mà hai góc ở vị trí so le trong nên AB // CE.
Mặt khác (chứng minh câu b) và hai góc này ở vị trí so le trong nên AB // CD.
Qua điểm C, có CE // AB và CD // AB nên theo tiên đề Euclid ta có CE trùng CD
Hay ba điểm E, C, D thẳng hàng.
Lại có CE = CD (cùng bằng AB)
Từ đó suy ra C là trung điểm của DE.
Bài 4.
a) Trục đứng ở biểu đồ trên biểu diễn số lượng (nghìn) vé bán được ở sân vận động A và sân vận động B từ năm 2017 đến năm 2021. Dữ liệu về đại lượng này là dữ liệu số.
b) Bảng thống kê như sau:
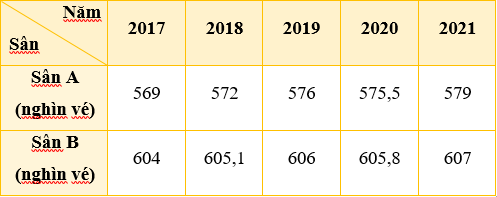
c) Quan sát biểu đồ trên, ta thấy đường nối bởi các điểm hình vuông luôn nằm trên đường nối bởi các điểm hình thoi nên sân vận động B bán được nhiều vé hơn sân vận động A.
Bài 5.
Số tiền cửa hàng nhập cam về là:
20 . 15 = 300 (nghìn đồng)
• Xét phương án 1:
Cửa hàng bán 8 kg cam đầu tiên với giá niêm yết 22 000 đồng/kg thì thu được số tiền là:
8 . 22 = 176 (nghìn đồng)
Cửa hàng bán 12 kg còn lại với giá giảm 15% so với giá niêm yết thì thu được số tiền là:
12 . (100% – 15%) . 22 = 224,4 (nghìn đồng)
Tiền lãi cửa hàng thu được sau khi bán một lô cam là:
176 + 224,4 – 300 = 100,4 (nghìn đồng).
• Xét phương án 2:
Cửa hàng bán 5 kg cam đầu tiên với giá giảm 7% so với giá niêm yết thì thu được số tiền là:
5 . (100% – 7%) . 22 = 102,3 (nghìn đồng)
Cửa hàng bán 9 kg cam tiếp theo với giá giảm 10% so với giá niêm yết thì thu được số tiền là:
9 . (100% – 10%) . 22 = 178,2 (nghìn đồng)
Cửa hàng bán 6 kg cam cuối cùng với giá giảm 15% so với giá niêm yết thì thu được số tiền là:
6 . (100% – 15%) . 22 = 112,2 (nghìn đồng)
Tiền lãi cửa hàng thu được sau khi bán một lô cam là:
102,3 + 178,2 + 112,2 – 300 = 92,7 (nghìn đồng).
• Xét phương án 3:
Cửa hàng bán 20 kg còn lại với giá giảm 10% so với giá niêm yết thì thu được số tiền là:
20 . (100% – 10%) . 22 = 396 (nghìn đồng)
Tiền lãi cửa hàng thu được sau khi bán một lô cam là:
396 – 300 = 96 (nghìn đồng).
• Ta thấy 100,4 > 96 > 92,7 nên theo phương án 1 thì cửa hàng thu được nhiều lãi nhất.
Vậy cửa hàng nên chọn phương án 1 mà quản lí đã đưa ra để có lãi nhất.
Bộ 10 đề thi học kì 1 Toán lớp 7 Kết nối tri thức có đáp án - Đề 3
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Kết nối tri thức
Năm học ................
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 3)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Số hữu tỉ là số viết được dưới dạng phân số với:
A. a = 0, b ≠ 0;
B. a, b ∈ ℤ; b ≠ 0;
C. a, b ∈ ℕ;
D. a ∈ ℕ; ; b ≠ 0.
Câu 2. Số đối của số hữu tỉ là
A. ;
B.
C.
D.
Câu 3. Dạng số thập phân hữu hạn của phân số là:
A. 0,(66);
B. – 0,(6);
C.
D. 0,6.
Câu 4. Căn bậc hai số học của là:
A.
B.
C.
D.
Câu 5. Nhận định nào sau đây là đúng?
A. 1,516 < 1,(516);
B. 1,516 = 1,(516);
C. 1,516 > 1,(516);
D. 1,516 ≈ 1,(516).
Câu 6. Cho hình vẽ
Chọn khẳng định đúng:
A. OA là tia phân giác của ;
B. OB là tia phân giác của ;
C. OC là tia phân giác của ;
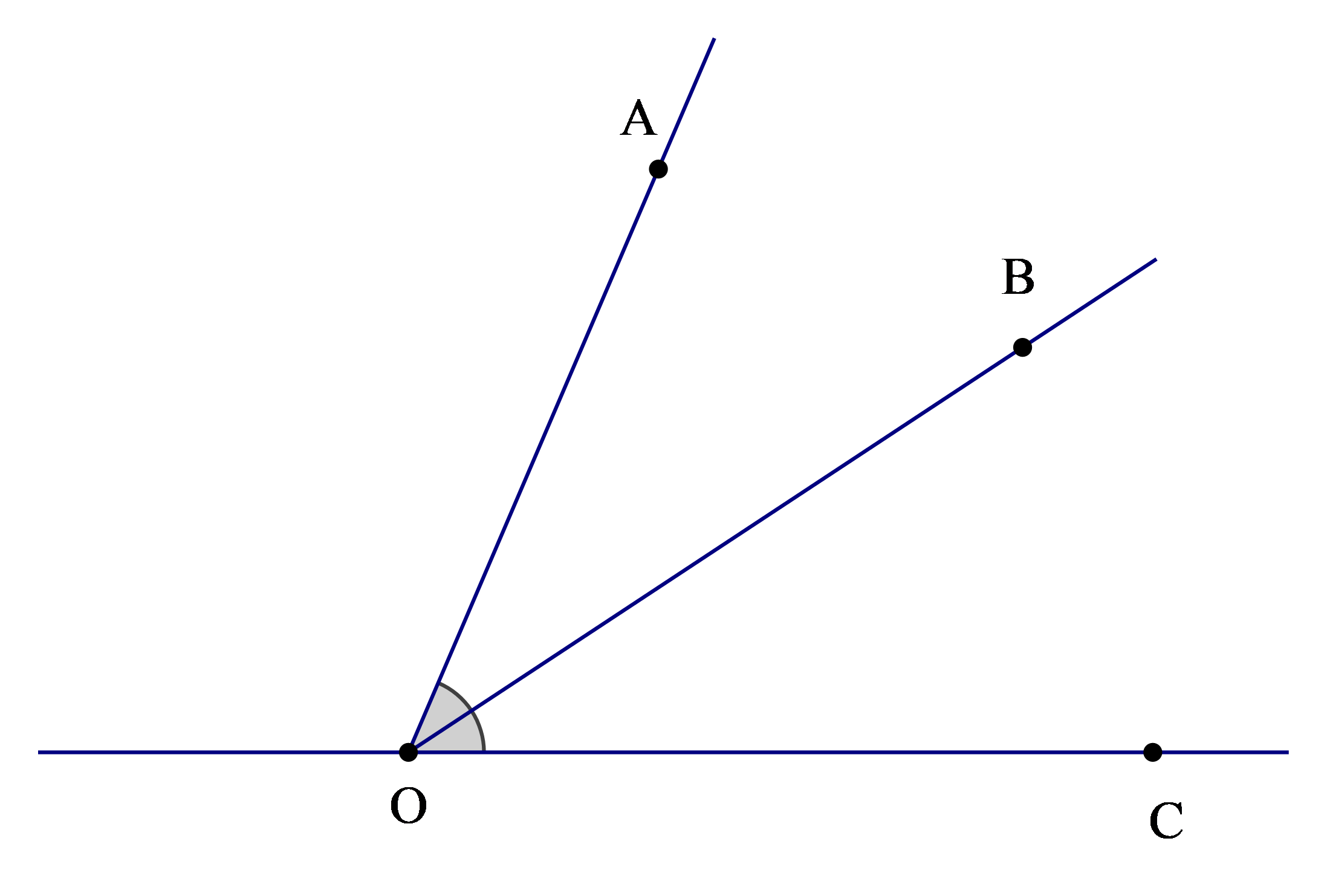
D. Cả 3 phương án đều đúng.
Câu 7. Chọn cách viết đúng giả thiết và kết luận của định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.”
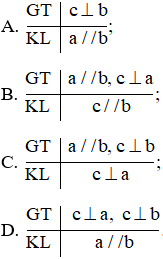
Câu 8. Tam giác ABC vuông tại A thì:
A.
B.
C.
D.
Câu 9. Cho DABC = DA’B’C’. Trong các khẳng định sau, khẳng định nào là đúng?
A. Hai đỉnh A và A’ gọi là hai đỉnh tương ứng;
B. Hai góc B và C’ gọi là hai góc tương ứng;
C. Hai cạnh AC và A’B’ gọi là hai cạnh tương ứng;
D. Hai cạnh AB và B’C’ gọi là hai cạnh tương ứng.
Câu 10. Điền vào chỗ chấm:
Đường thẳng … một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng ấy.
A. vuông góc với, một điểm;
B. cắt, một điểm;
C. cắt, trung điểm;
D. vuông góc với, trung điểm.
Câu 11. Dãy dữ liệu về cân nặng (đơn vị: kilôgam) của 7 học sinh lớp 7A: 25; 30; 32; 28; 29; 31; 27 thuộc loại dữ liệu nào?
A. Dữ liệu không là số;
B. Dữ liệu định tính;
C. Dữ liệu định lượng;
D. Dữ liệu kilôgam.
Câu 12. Thầy giáo muốn điều tra môn thể thao yêu thích của học sinh khối lớp 7 (gồm ba lớp 7A, 7B, 7C). Cách điều tra nào sau đây đảm bảo được tính đại diện?
A. Lấy ý kiến của các bạn nam;
B. Lấy ý kiến của các bạn nữ;
C. Lấy ý kiến của các bạn lớp 7A;
D. Lấy ý kiến ngẫu nhiên của các bạn trong cả ba lớp 7A, 7B, 7C.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
1. Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
a)
b)
2. Tìm x, biết:
Bài 2. (0,5 điểm) Cho biết 1 m = 3,28 feet. Hỏi một chú dơi Kitti dài 0,83 feet thì dài khoảng bao nhiêu xăngtimét (lấy độ chính xác d = 0,005)?
Bài 3. (3,0 điểm) Cho tam giác ABC. Gọi I là trung điểm của AB. Trên tia đối của tia IC, lấy điểm M sao cho IM = IC.
a) Chứng minh rằng DAIM = DBIC. Từ đó suy ra AM = BC và AM // BC.
b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh AN // BC.
c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
Bài 4. (1,0 điểm) Một nghiên cứu đã đưa ra tỉ lệ học sinh cấp THCS nghiện điện thoại di động trong những năm gần đây như biểu đồ sau:
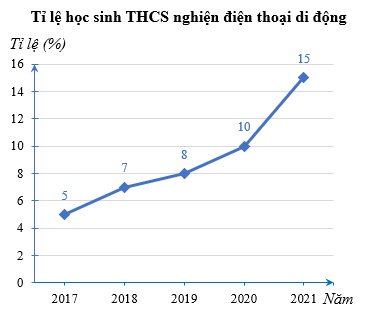
a) Trục đứng biểu diễn đại lượng gì? Dữ liệu về đại lượng này thuộc loại nào?
b) Năm 2021, một trường THCS có 600 học sinh. Hãy ước lượng số học sinh nghiện điện thoại di động của trường THCS đó.
Bài 5. (1,0 điểm) Giá niêm yết của một chiếc điện thoại tại một cửa hàng vào tháng 10 là 12 000 000 đồng. Cứ sau một tháng thì giá của điện thoại lại giảm 5% so với giá bán niêm yết ở tháng trước. Sau hai tháng, cửa hàng bán chiếc điện thoại đó vẫn nhận được lãi 830 000 đồng so với giá nhập về. Hỏi giá nhập về của chiếc điện thoại này là bao nhiêu?
Đáp án đề thi Học kì 1 môn Toán lớp 7 Kết nối tri thức - (Đề số 3)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
B |
C |
D |
C |
A |
B |
C |
B |
A |
C |
C |
D |
Hướng dẫn giải phần trắc nghiệm
Câu 1.
Đáp án đúng là: B
Số hữu tỉ là số viết được dưới dạng phân số với a, b ∈ ℤ; b ≠ 0.
Vậy ta chọn phương án B.
Câu 2.
Đáp án đúng là: C
Ta Số đối của số hữu tỉ là
Vậy ta chọn phương án C.
Câu 3.
Đáp án đúng là: D
Ta có
Vậy ta chọn phương án C.
Câu 4.
Đáp án đúng là: C
Ta có
Vậy ta chọn phương án C.
Câu 5.
Đáp án đúng là: A
Ta có 1,516 = 1,51600… và 1,(516) = 1,516516…
So sánh 1,51600… và 1,516516… ta thấy cặp chữ số cùng hàng đầu tiên khác nhau của hai số là hàng phần chục nghìn.
Do 0 < 5 nên 1,51600… < 1,516516… hay 1,516 < 1,(516).
Vậy ta chọn phương án A.
Câu 6.
Đáp án đúng là: B
Vì tia OB nằm giữa hai tia OA và OC nên tạo thành hai góc tương ứng là và
Mà
Do đó OB là tia phân giác của
Vậy ta chọn phương án B.
Câu 7.
Đáp án đúng là: C
Giả thiết và kết luận của định lí là:
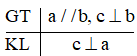
Vậy ta chọn phương án C.
Câu 8.
Đáp án đúng là: B
Tam giác ABC vuông tại A nên ta có (trong tam giác vuông, hai góc nhọn phụ nhau).
Vậy ta chọn phương án B.
Câu 9.
Đáp án đúng là: A
Từ DABC = DA’B’C’ ta có:
• Hai đỉnh A và A’ là hai đỉnh tương ứng;
• Hai góc B và B’ là hai góc tương ứng;
Hai góc C và C’ là hai góc tương ứng;
• Hai cạnh AC và A’C’ là hai cạnh tương ứng;
Hai cạnh AB và A’B’ là hai cạnh tương ứng;
Hai cạnh BC và B’C’ là hai cạnh tương ứng.
Vậy ta chọn phương án A.
Câu 10.
Đáp án đúng là: C
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.
Vậy ta chọn phương án C.
Câu 11.
Đáp án đúng là: C
Dãy dữ liệu về cân nặng (đơn vị: kilôgam) của 7 học sinh lớp 7A là dãy dữ liệu số, hay là dữ liệu định lượng.
Vậy ta chọn phương án C.
Câu 12.
Đáp án đúng là: D
Để đảm bảo được tính đại diện thì các học sinh được chọn một cách ngẫu nhiên.
Vậy cách điều tra cần chọn trong các cách trên là lấy ý kiến ngẫu nhiên của các bạn trong cả ba lớp 7A, 7B, 7C.
PHẦN II. TỰ LUẬN (7,0 điểm)
Hướng dẫn giải phần tự luận
Bài 1.
1.1.
a)
b)
1.2.
Vậy
Bài 2.
Cho biết 1 m = 3,28 feet. Hỏi một chú dơi Kitti dài 0,83 feet thì dài khoảng bao nhiêu xăngtimét (lấy độ chính xác d = 0,005)?
Đổi 1 m = 100 cm = 3,28 feet.
Khi đó 1 feet sẽ bằng (cm).
Chú dơi Kitti dài 0,83 feet thì dài (cm).
Với độ chính xác d = 0,005, ta làm tròn kết quả tới hàng phần trăm được 25,30 (cm).
Vậy chú dơi Kitti dài 0,83 feet thì dài khoảng 25,30 cm.
Bài 3.
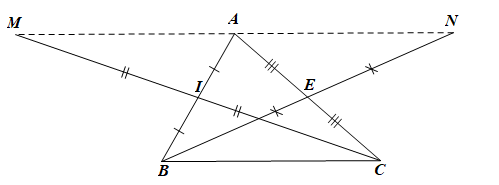
a) Xét DAIM và DBIC có:
IA = IB (do I là trung điểm của AB);
(hai góc đối đỉnh);
IM = IC (giả thiết).
Do đó DAIM = DBIC (c.g.c)
Suy ra AM = BC (hai cạnh tương ứng) và (hai góc tương ứng)
Mà là hai góc ở vị trí so le trong nên AM // BC.
b) Xét DANE và DCBE có:
EA = EC (do E là trung điểm của AC);
(hai góc đối đỉnh);
EN = EB (giả thiết).
Do đó DANE = DCBE (c.g.c)
Suy ra (hai góc tương ứng)
Mà là hai góc ở vị trí so le trong nên AN // BC.
c) Ta có AM // BC (theo câu a) và AN // BC (theo câu b)
Do đó qua điểm A có hai đường thẳng song song với BC nên theo tiên đề Euclid, hai đường thẳng AM và AN trùng nhau hay ba điểm A, M, N thẳng hàng.
Lại có DANE = DCBE (theo câu b) nên AN = CB (hai cạnh tương ứng)
Mặt khác AM = BC (theo câu a)
Do đó AM = AN (cùng bằng BC)
Mà ba điểm A, M, N thẳng hàng nên A là trung điểm của MN.
Bài 4.
a) Trục đứng biểu diễn tỉ lệ học sinh THCS nghiện điện thoại di dộng. Dữ liệu này là dữ liệu số.
b) Quan sát biểu đồ ta thấy, tỉ lệ học sinh THCS nghiện điện thoại di dộng năm 2021 là 15%
Số học sinh của trường THCS đó nghiện điện thoại di dộng khoảng:
600 . 15% = 600 . = 90 (học sinh).
Bài 5.
Giá bán của chiếc điện thoại ở tháng 11 là:
12 000 000 . (100% – 5%) = 11 400 000 (đồng).
Giá bán của chiếc điện thoại ở tháng 12 là:
11 400 000 . (100% – 5%) = 10 830 000 (đồng).
Sau hai tháng, cửa hàng vẫn lãi 830 000 đồng so với giá nhập về nên giá nhập về là:
10 830 000 – 830 000 = 10 000 000 (đồng).
Vậy giá nhập về của chiếc điện thoại này là 10 000 000 đồng.
Bộ 10 đề thi học kì 1 Toán lớp 7 Kết nối tri thức có đáp án - Đề 4
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Kết nối tri thức
Năm học ................
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 4)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Số nào dưới đây là số hữu tỉ âm?
A.
B.
C.
D.
Câu 2. Phân số biểu diễn số hữu tỉ – 3,25 là
A.
B.
C.
D.
Câu 3. Phân số được viết dưới dạng số thập phân vô hạn tuần hoàn là
A. 0,3838…;
B. 0,8333;
C. 0,(3)8;
D. 0,(8)3.
Câu 4. Có bao nhiêu số vô tỉ trong các số
A. 1;
B. 2;
C. 3;
D. 4.
Câu 5. Giá trị của biểu thức A = |– 120| + |20| là
A. –100;
B. 100;
C. –140;
D. 140.
Câu 6. Khẳng định nào dưới đây là đúng?
A. Hai góc đối đỉnh thì phụ nhau;
B. Hai góc đối đỉnh thì bằng nhau;
C. Hai góc đối đỉnh thì bù nhau;
D. Hai góc đối đỉnh thì kề nhau.
Câu 7. Điền vào chỗ trống để phát biểu sau là khẳng định đúng:
“Qua một điểm nằm ngoài một đường thẳng … đường thẳng song song với đường thẳng đó”.
A. không có;
B. có duy nhất một;
C. có hai;
D. có vô số.
Câu 8. Tam giác ABC vuông tại A. Phát biểu nào dưới đây là đúng khi nói về góc B?
A. Góc B là góc tù;
B. Góc B là góc vuông;
C. Góc B là góc nhọn;
D. Góc B là góc bẹt.
Câu 9. Cho tam giác ABC và tam giác IHK có AB = IH, BC = HK. Cần thêm điều kiện gì để DABC = DIHK theo trường hợp cạnh – góc – cạnh?
A.
B.
C.
D. AC = IK.
Câu 10. Cho tam giác ABC có AB = 16 cm, AC = 25 cm. Vẽ đường trung trực của BC cắt AC tại D. Chu vi của tam giác ABD là
A. 41 cm;
B. 48 cm;
D. 51 cm;
D. Cả A, B, C đều sai.
Câu 11. Hãy cho biết dữ liệu về mức độ yêu thích môn Toán của các học sinh ở một trường THCS (từ không yêu thích đến rất yêu thích) thuộc loại dữ liệu nào?
A. Dữ liệu là số;
B. Dữ liệu không là số, không thể sắp thứ tự;
C. Dữ liệu không là số, có thể sắp thứ tự;
D. Không phải là dữ liệu.
Câu 12. Tỉ lệ các loại từ trong Tiếng Anh được biểu diễn trong biểu đồ dưới đây:
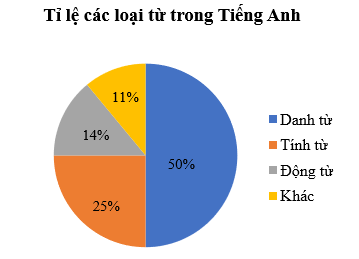
(Nguồn: http://lemongrad.com/english-language-statistics/)
Loại từ nào xuất hiện nhiều nhất trong Tiếng Anh?
A. Danh từ;
B. Tính từ;
C. Động từ;
D. Loại từ khác.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
1. Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
a)
b)
2. Tìm x, biết:
Bài 2. (0,75 điểm) Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 9 cm, chiều rộng là 6 cm. Tính độ dài đường chéo của hình chữ nhật (lấy kết quả với độ chính xác 0,005).
Bài 3. (3,0 điểm) Cho tam giác ABC có AB = AC, M là trung điểm của BC.
a) Chứng minh DAMB = DAMC.
b) Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Chứng minh tam giác ADE cân.
c) Trên tia đối của tia ED lấy điểm F sao cho EF = MC, gọi H là trung điểm của EC. Chứng minh ba điểm M, H, F thẳng hàng.
Bài 4. (1,0 điểm) Bản tin dịch COVID-19 ngày 12/12/2021 của Bộ Y tế cho biết số ca mắc bệnh ở một số tỉnh/ thành phố như bảng sau:
|
Số ca mắc COVID-19 ở một số tỉnh/ thành phố ngày 11/12/2021 |
||||
|
Tỉnh/thành phố |
Tp. Hồ Chí Minh |
Tây Ninh |
Đồng Tháp |
Cần Thơ |
|
Số ca mắc |
1 216 |
920 |
745 |
669 |
Hãy vẽ biểu đồ đoạn thẳng biểu diễn bảng thống kê trên.
Bài 5. (0,75 điểm) Một công ty phát triển kĩ thuật có một số thông báo rất hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 17 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:
– Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 170 triệu đồng;
– Phương án 2: Ngày đầu tiên nhận 3 đồng, ngày sau nhận gấp 3 lần ngày trước đó.
Em hãy giúp nhóm kỹ thuật viên lựa chọn phương án để nhận được nhiều tiền công hơn và giải thích tại sao chọn phương án đó.
Bộ 10 đề thi học kì 1 Toán lớp 7 Kết nối tri thức có đáp án - Đề 5
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Kết nối tri thức
Năm học ................
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 5)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Số đối của số là
A.
B.
C.
D.
Câu 2. Trong các phát biểu dưới đây, phát biểu nào sai?
A. Nếu a ∈ ℕ thì a ∈ ℚ;
B. Nếu a ∈ ℚ thì a ∈ ℤ;
C. Nếu a ∈ ℤ thì a ∈ ℚ;
D. Nếu a ∈ ℚ thì a ∉ ℕ.
Câu 3. Phân số nào dưới đây biểu diễn được dưới dạng số thập phân vô hạn tuần hoàn?
B.
C.
D.
Câu 4. Giá trị của biểu thức là
A.
B.
C.
D.
Câu 5. Nhận xét nào sau đây là sai?
A. |x| ≤ x với mọi x;
B. |x| ≥ x với mọi x;
C. |x| = x với x ≥ 0;
D. |x| = – x với x < 0.
Câu 6. Hai tia phân giác của hai góc đối đỉnh là
A. hai tia trùng nhau;
B. hai tia vuông góc;
C. hai tia đối nhau;
D. hai cạnh của góc 60°.
Câu 7. Cho định lí: “Hai đường thẳng a và b song song với nhau nếu hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc đồng vị bằng nhau”. Phần kết luận của định lí trên là
A. Hai đường thẳng a và b song song với nhau;
B. Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc đồng vị bằng nhau;
C. Trong các góc tạo thành có một cặp góc đồng vị bằng nhau;
D. Hai đường thẳng a, b cắt đường thẳng c.
Câu 8. Một tam giác cân có số đo góc ở đáy bằng 50°, số đo góc ở đỉnh là
A. 60°;
B. 80°;
C. 90°;
D. 100°.
Câu 9. Cho tam giác ABC và tam giác NPM có BC = PM, Cần thêm điều kiện gì để DABC = DNPM theo trường hợp cạnh huyền – cạnh góc vuông?
A. BA = PM;
B. BA = PN;
C. CA = MN;
D.
Câu 10. Cho tam giác ABC có Số đo của góc B là
A. 34°;
B. 35°;
C. 60°;
D. 90°.
Câu 11. Dữ liệu về số học sinh trong từng lớp học thuộc loại dữ liệu nào?
A. Dữ liệu là số;
B. Dữ liệu không là số, có thể sắp thứ tự;
C. Dữ liệu không là số, không thể sắp thứ tự;
D. Không phải là dữ liệu.
Câu 12. Dữ liệu nào sau đây là dữ liệu định tính?
A. Số dân của các nước Đông Nam Á;
B. Màu sắc yêu thích của học sinh lớp 7A;
C. Nhiệt độ trung bình (đơn vị: độ C) trong một tuần của thành phố Đà Nẵng;
D. Số lượng ti vi bán được trong một tuần của cửa hàng.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
1. Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
a)
b)
2. Tìm x, biết:
Bài 2. (0,5 điểm) Một khu vườn hình vuông có diện tích 200 m2. Tính độ dài mỗi cạnh của khu vườn với độ chính xác 0,005.
Bài 3. (3,0 điểm) Cho tam giác ABC vuông tại A (AB < AC). Vẽ AH ⊥ BC (H ∈ BC). Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA.
a) Chứng minh rằng DBAH = DBDH và tia BC là tia phân giác của góc ABD.
b) Qua D vẽ đường thẳng song song với AB, cắt BC tại M và cắt AC tại K. Chứng minh rằng AD là đường trung trực của đoạn thẳng BM.
c) Vẽ đường thẳng CN vuông góc với đường thẳng AM (N ∈ AM). Chứng minh ba điểm C, N, D thẳng hàng.
Bài 4. (1,0 điểm) Quan sát biểu đồ đoạn thẳng sau:
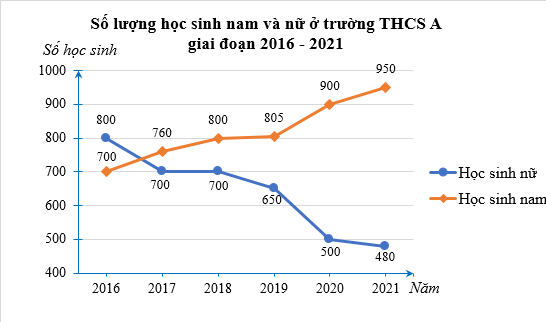
a) Biểu đồ trên cho ta biết thông tin gì?
b) Trong giai đoạn 2016 – 2021, năm nào trường THCS A có số học sinh nữ cao hơn số học sinh nam?
c) Xác định xu thế tăng, giảm số học sinh nam và nữ của trường THCS A đó trong giai đoạn 2016 – 2021.
Bài 5. (1,0 điểm) Tìm giá trị nhỏ nhất của biểu thức M = |x – 22| + |x + 12|.
Bộ 10 đề thi học kì 1 Toán lớp 7 Kết nối tri thức có đáp án - Đề 6
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Kết nối tri thức
Năm học ................
Môn: Toán 7
Thời gian làm bài: 90 phút
(Đề số 6)
Câu 1 : Căn bậc hai số học của 16 là
Câu 2 : Số nào là số vô tỉ trong các số sau:
Câu 3 : Trong các số sau có bao nhiêu số hữu tỉ dương?
Câu 4 : Kết quả của phép tính là:
Câu 5 : Cho = 25 thì giá trị của x là:
Câu 6 : Kết quả làm tròn số 17,8569 đến hàng phần trăm là:
Câu 7 : Cho điểm thuộc trung trực của đoạn thẳng . Biết . Độ dài đoạn thẳng là
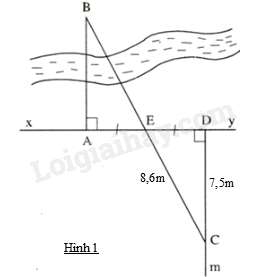
Câu 8 : Trên hình 1, khoảng cách giữa hai địa điểm và là bao nhiêu ?
Câu 9 : Một tam giác cân có số đo góc ở đáy gấp hai lần số đo góc ở đỉnh. Số đo góc ở đỉnh của tam giác cân đó là:
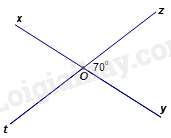
Câu 10 : Trong hình vẽ dưới đây, góc xOt có số đo bằng:
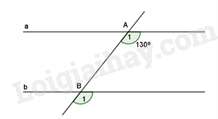
Câu 11 : Cho hình vẽ bên, biết a // b. Số đo là:
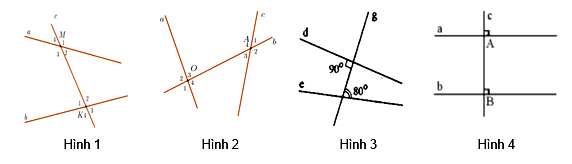
Câu 12 : Hình vẽ nào sau đây có hai đường thẳng song song?
Câu 1 : Thực hiện phép tính (Tính hợp lý nếu có thể):
a)
b)
Câu 2 : Tìm số hữu tỉ x biết:
Câu 3 : Tại cửa hàng bán hoa, giá bán ban đầu của một bó hoa là 80 000 đồng. Vào ngày Quốc tế phụ nữ 8/3, cửa hàng đã quyết định giảm giá 20% cho mỗi bó hoa so với giá bán ban đầu và nếu khách hàng mua 10 bó trở lên thì từ bó thứ 10 trở đi, mỗi bó hoa khách hàng sẽ chỉ phải trả với giá bằng 75% của giá đã giảm trước đó. Một công ty muốn đặt 50 bó hoa để tặng cho các nhân viên nữ. Tính tổng số tiền công ty phải trả.
Câu 4 : Cho biểu đồ sau:
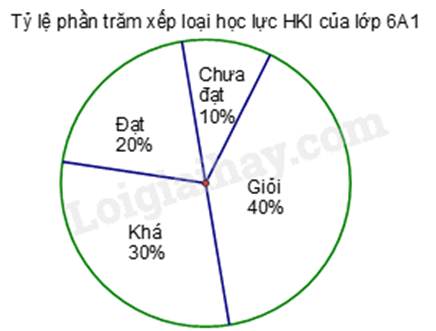
a) Biểu đồ biểu diễn thông tin về vấn đề gì? Tỉ lệ % của mỗi đối tượng so với toàn thể là bao nhiêu?
b) Tính tổng số học sinh giỏi và khá của lớp 6A1 biết lớp có 50 học sinh.
Câu 5 : Cho có . Trên tia BA lấy điểm D sao cho . Tia phân giác cắt AC ở E. Gọi K là trung điểm của DC.
a) Chứng minh .
b) Chứng minh .
c) Chứng minh B, K, E thẳng hàng.
d) Kẻ . cần thêm điều kiện gì để .
ĐÁP ÁN
| Câu 1-B | Câu 2-A | Câu 3-C | Câu 4-A |
| Câu 5-D | Câu 6-C | Câu 7-A | Câu 8-A |
| Câu 9-B | Câu 10-B | Câu 11-C | Câu 12-D |
Câu 1 :
a)
b)
Câu 2 :
Suy ra hoặc
TH1.
TH2.
Vậy .
Câu 3 :
Giá 1 bó hoa sau khi giảm 20%: 80 000.80% = 64000 đồng
Giá 1 bó hoa từ bó thứ 10 trở đi: 64 000.75% = 48000 đồng
Vậy tổng số tiền công ty phải trả khi mua 50 bó hoa:
64 000.9 + 48000.41 = 2 544 000 đồng
Câu 4 :
a) Biểu đồ biểu diễn "Tỉ lệ phần trăm xếp loại học lực HKI của lớp 9A1".
Bảng biểu diễn tỉ lệ % của mỗi đối tượng :

(Có thể lựa chọn vẽ bảng hoặc liệt kê phần trăm)
b) Tổng số phần trăm học sinh giỏi và khá là : 40% + 30% = 70%.
Số học sinh giỏi và khá của lớp 6A1 là : 50.70% = 35 (học sinh).
Câu 5 :
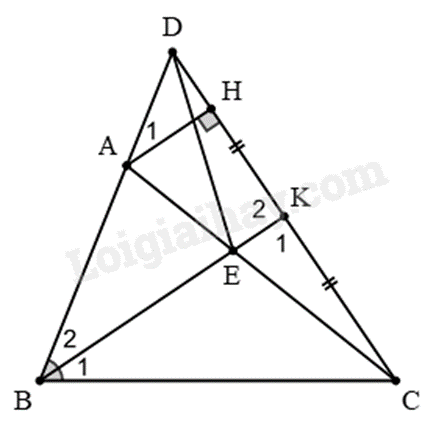
a) Xét và có:
BD = BC (gt)
(BE là tia phân giác của )
BE chung
(c.g.c) (đpcm)
(hai cạnh tương ứng)
b) Xét và có:
ED = EC (cmt)
EK chung
DK = KC (K là trung điểm của DC)
(c.c.c)
(hai cặp góc tương ứng)
Mà và là hai góc kề bù nên hay . (1) (đpcm)
c) Xét và có:
BD = BC (gt)
BK chung
DK = KC (K là trung điểm của DC)
(c.c.c)
(hai cặp góc tương ứng)
Mà và là hai góc kề bù nên hay (2)
Từ (1) và (2) suy ra B, E, K thẳng hàng. (đpcm)
d) Ta có: ;
(hai góc đồng vị).
Để thì , mà nên hay tam giác ABC vuông tại B.
Vậy tam giác ABC tam giác cân tại B thì ta có .