Với tóm tắt lý thuyết Toán lớp 10 Chương 1: Mệnh đề và Tập hợp sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.
Lý thuyết Toán lớp 10 Chương 1: Mệnh đề và Tập hợp
A. Lý thuyết Chương 1: Mệnh đề và Tập hợp
1. Mệnh đề, mệnh đề chứa biến
1.1. Mệnh đề
- Những khẳng định có tính đúng hoặc sai gọi là mệnh đề logic (gọi tắt là mệnh đề). Những câu không xác định được tính đúng sai không phải là mệnh đề.
- Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai.
Ví dụ 1:
Câu “Hoa hồng rất đẹp nhất trong các loài hoa” là câu khẳng định nhưng không xác định được tính đúng sai nên câu này không là mệnh đề.
Câu “Bây giờ là mấy giờ?” là một câu hỏi không xác định được tính đúng sai nên câu này không là mệnh đề.
Câu “8 + 1 > 9” là một câu khẳng định có thể xác định được tính đúng sai nên câu này là mệnh đề.
Câu “Số 1 tỉ là số rất lớn” là một câu khẳng định tuy nhiên câu này mang tính quan điểm cá nhân không xác định đước tính đúng sai nên không là mệnh đề.
Chú ý:
- Người ta thường sử dụng các chữ cái P, Q, R, … để biểu thị các mệnh đề.
- Những mệnh đề liên quan đến toán học được gọi là mệnh đề toán học.
- Những câu nghi vấn, câu cảm thán, câu cầu khiến không phải là mệnh đề.
Ví dụ 2:
+ “Hà Nội là thủ đô của Việt Nam” là một mệnh đề nhưng không phải mệnh đề toán học vì không phải sự kiện trong toán học.
+ “Số π là một số hữu tỉ” là mệnh đề toán học.
1.2. Mệnh đề chứa biến
- Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập D nào đó mà với mỗi giá trị của biến thuộc vào D ta được một mệnh đề.
- Ta thường kí hiệu mệnh đề chứa biến n là P(n); mệnh đề chứa biến x, y là P(x, y), ….
Ví dụ:
+ “Với mọi giá trị thực của biến x, |x| ≥ x”: không phải là mệnh đề chứa biến vì:
Ta có |x| ≥ x với mọi giá trị thực của biến x nên đây là khẳng định đúng. Do đó phát biểu này là một mệnh đề không phải mệnh đề chứa biến.
+ “5n chia hết cho 2” là mệnh đề chứa biến.
Khi n = 4 thì mệnh đề này là mệnh đề đúng, khi n = 5 thì mệnh đề này là mệnh đề sai.
2. Mệnh đề phủ định
- Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Ta kí hiệu mệnh đề phủ định của mệnh đề P là .
- Mệnh đề P và mệnh đề là hai phát biểu trái ngược nhau. Nếu P đúng thì sai, còn nếu P sai thì đúng.
Ví dụ: “5 không chia hết cho 3” là mệnh đề phủ định của mệnh đề “5 chia hết cho 3”;
“3 là hợp số” là mệnh đề phủ định của mệnh đề “3 không là hợp số”.
3. Mệnh đề kéo theo, mệnh đề đảo
3.1. Mệnh đề kéo theo
- Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo và kí hiệu là P ⇒ Q.
- Các định lí toán học là những mệnh đề đúng và thường có dạng P ⇒ Q. Khi đó ta nói:
P là giả thiết của định lí, Q là kết luận của định lí hoặc
“P là điều kiện đủ để có Q”, hoặc “Q là điều kiện cần để có P”.
Chú ý: Mệnh đề P ⇒ Q chỉ sai khi P đúng và Q sai. Do đó ta chỉ cần xét tính đúng sai của mệnh đề P ⇒ Q khi P đúng. Khi đó, nếu Q đúng thì P ⇒ Q đúng, nếu Q sai thì P ⇒ Q sai.
Ví dụ: Cho 2 mệnh đề: P: “9 chia hết cho 9”; Q: “9 chia hết cho 3”.
“Nếu 9 chia hết cho 9 thì 9 chia hết cho 3” là mệnh đề kéo theo của P và Q.
P là mệnh đề đúng và Q là mệnh đề đúng nên mệnh đề kéo theo P ⇒ Q là mệnh đề đúng.
3.2. Mệnh đề đảo
- Mệnh đề Q ⇒ P được gọi là mệnh đề đảo của mệnh đề P ⇒ Q.
Nhận xét: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
Ví dụ: Cho 2 mệnh đề: P: “n = 0”; Q: “n là số nguyên”.
Mệnh đề kéo theo P ⇒ Q được phát biểu là: “Nếu n = 0 thì n là số nguyên”.
Mệnh đề đảo Q ⇒ P được phát biểu là “Nếu n là số nguyên thì n = 0”.
- Mệnh đề P ⇒ Q là mệnh đề đúng còn mệnh đề Q ⇒ P không đúng.
4. Mệnh đề tương đương
- Mệnh đề “P nếu và chỉ nếu Q” được gọi là một mệnh đề tương đương và kí hiệu P ⇔ Q .
Nhận xét:
- Nếu cả hai mệnh đề Q ⇒ P và P ⇒ Q đều đúng thì hai mệnh đề tương đương P ⇔ Q đúng. Khi đó ta nói “P tương đương với Q” hoặc “P là điều kiện cần và đủ để có Q” hoặc “P khi và chỉ khi Q”.
Ví dụ: Cho 2 mệnh đề: P: “Tứ giác ABCD là hình bình hành”; Q: “Tứ giác ABCD có hai cặp cạnh đối song song”.
“Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai cặp cạnh đối song song” là mệnh đề P ⇒ Q.
“Nếu tứ giác ABCD có hai cặp cạnh đối song song thì tứ giác ABCD là hình bình hành” là mệnh đề Q ⇒ P.
Hai mệnh đề này đều đúng nên P và Q là hai mệnh đề tương đương.
Khi đó mệnh đề P ⇔ Q được phát biểu như sau: “Tứ giác ABCD là hình bình hành khi và chỉ khi tứ giác ABCD có hai cặp cạnh đối song song”.
5. Mệnh đề có chứa kí hiệu ∀ và ∃
- Kí hiệu ∀ đọc là “với mọi”.
- Kí hiệu ∃ đọc là “có một” hoặc “tồn tại”.
- Cho mệnh đề “ ”.
+ Phủ định của mệnh đề “ ” là mệnh đề “ ”.
+ Phủ định của mệnh đề “ ” là mệnh đề “ ”.
Chú ý:
+ Phát biểu “Với mọi số tự nhiên n” có thể kí hiệu là .
+ Phát biểu “Tồn tại số tự nhiên n” có thể kí hiệu là .
Ví dụ:
Phủ định của mệnh đề “ ” là mệnh đề: “ ”.
6. Các khái niệm cơ bản về tập hợp
6.1. Tập hợp
• Có thể mô tả một tập hợp bằng một trong hai cách sau:
Cách 1. Liệt kê các phần tử của tập hợp;
Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
ü a ∈ S: phần tử a thuộc tập hợp S.
ü a ∉ S: phần tử a không thuộc tập hợp S.
Chú ý: Số phần tử của tập hợp S được kí hiệu là n(S).
Ví dụ:
- Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2, lớn hơn 5 và nhỏ hơn 15.
+ Ta mô tả tập hợp A bằng hai cách như sau:
Cách 1: Liệt kê các phần tử của tập hợp: A = {6; 8; 10; 12; 14};
Cách 2: Chỉ ra tính chất đặc trưng của các phẩn tử: A = { | n ⁝ 2, 5 < n < 15}.
+ Tập hợp A có 5 phần tử, ta viết: n(A) = 5.
+ 10 thuộc tập hợp A, ta viết 10 ∈ A.
+ 15 không thuộc tập hợp A, ta viết 15 ∉ A.
• Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là .
Ví dụ:
+ Tập hợp các nghiệm của phương trình x2 + 1 = 0 là tập rỗng;
+ Tập hợp những người sống trên Mặt Trời là tập rỗng.
6.2. Tập hợp con
• Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và viết là T ⊂ S (đọc là T chứa trong S hoặc T là tập con của S).
- Thay cho T ⊂ S, ta còn viết S ⊃ T (đọc là S chứa T).
- Kí hiệu T ⊄ S để chỉ T không là tập con của S.
Nhận xét:
- Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng:
∀ x, x ∈ T ⇒ x ∈ S.
- Quy ước tập rỗng là tập con của mọi tập hợp.
• Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.
Minh họa T là một tập con của S như sau:
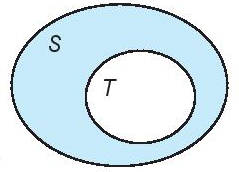
Ví dụ: Cho các tập hợp: T = {2; 3; 5}, S = {2; 3; 5; 7; 9}, M = {2; 3; 4; 5}.
- Tập hợp T là tập con của tập hợp S (do mọi phần tử của T đều thuộc S).
- Tập hợp M không là tập hợp con của tập hợp S (do có phần tử 4 thuộc M nhưng không thuộc S).
6.3. Hai tập hợp bằng nhau
- Hai tập hợp S và T được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần tử của tập hợp S và ngược lại. Kí hiệu là S = T.
- Nếu S ⊂ T và T ⊂ S thì S = T.
Ví dụ: Cho 2 tập hợp: S = {n | n là bội chung của 2 và 3; n < 20} và T = {n | n là bội của 6; n < 20}.
Ta có: S = {0; 6; 12; 18};
T = {0; 6; 12; 18}.
Vậy S = T.
7. Các tập hợp số
7.1. Mối quan hệ giữa các tập hợp số
- Tập hợp các số tự nhiên ℕ = {0; 1; 2; 3; 4; ....}.
- Tập hợp các số nguyên ℤ gồm các số tự nhiên và số nguyên âm:
ℤ = {...; – 3; – 2; – 1; 0; 1; 2; 3}.
- Tập hợp các số hữu tỉ ℚ gồm các số được viết dưới dạng phân số , với a, b ∈ ℤ, b ≠ 0.
Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
- Tập hợp các số thực ℝ gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn.
- Mối quan hệ giữa các tập hợp số: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.
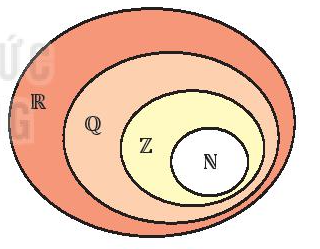
Ví dụ: Cho tập hợp B = {– 1; 2; 4; 10}.
- Tập hợp B chứa số – 1 không phải là số tự nhiên nên B không là tập con của ℕ.
- Tập hợp B gồm các số nguyên: – 1; 2; 4; 10 nên B là tập con của ℤ.
- Các số nguyên cũng là các số hữu tỉ và cũng là các số thực, nên B cũng là tập con của ℚ và ℝ.
7.2. Các tập con thường dùng của ℝ
- Một số tập con thường dùng của tập số thực ℝ:
+ Khoảng:




+ Đoạn

+ Nửa khoảng




- Kí hiệu + ∞: Đọc là dương vô cực (hoặc dương vô cùng).
- Kí hiệu – ∞: Đọc là âm vô cực (hoặc âm vô cùng).
- a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.
Ví dụ:
+ Ta có: 5 < x ≤ 10 thì ta viết x ∈ (5; 10].
+ Ta có: D = {x | x < 3} = (– ∞; 3).
8. Các phép toán trên tập hợp
8.1. Giao của hai tập hợp
Tập hợp gồm các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T, kí hiệu là S ∩ T.
S ∩ T ={x | x ∈ S và x ∈ T}.
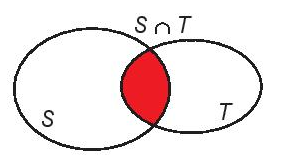
Ví dụ: Cho 2 tập hợp: A = {5; 7; 8} và B = {1; 2; 4; 5; 8}.
Giao của 2 tập hợp trên là tập hợp C = A ∩ B = {5; 8}.
8.2. Hợp của hai tập hợp
- Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T gọi là hợp của hai tập hợp S và T, kí hiệu là S ∪ T.
S ∪ T = {x | x ∈ S hoặc x ∈ T}.
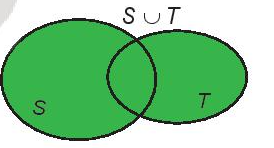
Ví dụ: Cho 2 tập hợp: S = {1; 2; 3; 5} và T = {2; 4; 6; 7}.
Tập hợp là hợp của hai tập hợp trên là K = S ∪ T = {1; 2; 3; 4; 5; 6; 7}.
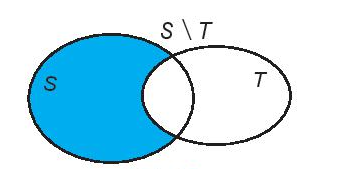
8.3. Hiệu của hai tập hợp
- Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc S nhưng không thuộc T, kí hiệu là S \ T.
S \ T = {x | x ∈ S và x ∉ T}.
- Nếu T ⊂ S thì S \ T được gọi là phần bù của T trong S, kí hiệu CST.
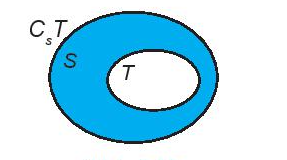
Chú ý: .
Ví dụ: Cho các tập hợp: S = {1; 2; 3; 4; 5; 7; 8}; T = {4; 5; 6; 7; 8; 9}; X = {x | x là các số nguyên dương nhỏ hơn 9}.
Ta có: S \ T = {1; 2; 3};
T \ S = {6; 9}.
Lại có: X = {1; 2; 3; 4; 5; 6; 7; 8}
Vì mọi phần tử của tập S đều thuộc tập X nên S ⊂ X.
Phần bù của S trong X là X \ S = CXS = {6}.
B. Bài tập tự luyện
B1. Bài tập tự luận
Bài 1. Cho các tập hợp: và .
a) Viết tập hợp A và B bằng cách liệt kê các phần tử của tập hợp.
b) Xác định các tập hợp A ∩ B, A ∪ B, A \ B, B \ A.
Hướng dẫn giải
a) Vì nên A là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 10.
Do đó: A = {0; 3; 6; 9}.
Vì nên B là tập hợp các số tự nhiên chia hết cho 2 và nhỏ hơn 10.
Do đó: B = {0; 2; 4; 6; 8}.
b) A ∩ B = {x | x ∈ A và x ∈ B} = {0; 6};
A ∪ B = {x | x ∈ A hoặc x ∈ B} = {0; 2; 3; 4; 6; 8; 9};
A \ B = {x | x ∈ A và x ∉ B} = {3; 9};
B \ A = {x | x ∈ B và x ∉ A} = {2; 4; 8}.
Bài 2. Phát biểu các mệnh đề sau và lập mệnh đề phủ định của nó dưới dạng kí hiệu:
a) P(x): “ ”.
b) Q(x): “ ”.
Hướng dẫn giải
a)
+ Phát biểu mệnh đề P(x): “Mọi số nguyên đều có bình phương lớn hơn hoặc bằng 0”.
+ Phủ định của mệnh đề P(x) là : “ ”.
b)
+ Phát biểu mệnh đề Q(x): “Có một số nguyên nhỏ hơn 0”.
+ Phủ định của mệnh đề Q(x) là : “ ”.
Bài 3. Cho tứ giác ABCD. Xét tính đúng sai của mệnh đề P ⇒ Q với:
a) P: “ABCD là một hình vuông”,
Q: “ABCD là một hình bình hành”;
b) P: “ABCD là một hình thoi”,
Q: “ABCD là một hình chữ nhật”.
Hướng dẫn giải
a) Mệnh đề P ⇒ Q: “Nếu ABCD là một hình vuông thì ABCD là một hình bình hành”. Mệnh đề này là mệnh đề đúng.
b) Mệnh đề P ⇒ Q: “Nếu ABCD là một hình thoi thì ABCD là một hình chữ nhật”. Mệnh đề này là mệnh đề sai.
Bài 4. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề phủ định đó:
a) “Số 50 chia hết cho 3”.
b) “Số 10 là hợp số”.
Hướng dẫn giải
a) Mệnh đề phủ định của mệnh đề “Số 50 chia hết cho 3” là “Số 50 không chia hết cho 3”. Mệnh đề phủ định này là mệnh đề đúng.
b) Mệnh đề phủ định của mệnh đề “Số 10 là hợp số” là “Số 10 không phải là hợp số”. Mệnh đề phủ định này là mệnh đề sai.
Bài 5. Những quan hệ nào trong các quan hệ sau đây là đúng?
a) A ⊂ (A ∪ B);
b) A ⊂ (A ∩ B);
c) (A ∩ B) ⊂ (A ∪ B);
d) (A ∪ B) ⊂ B;
e) (A ∩ B) ⊂ A.
Hướng dẫn giải
a) A ⊂ (A ∪ B) đúng vì A ∪ B chứa toàn bộ các phần tử của tập hợp A.
b) A ⊂ (A ∩ B) sai vì A ∩ B chỉ chứa những phần tử chung của A và B.
Sửa lại (A ∩ B) ⊂ A.
c) (A ∩ B) ⊂ (A ∪ B) đúng.
d) (A ∪ B) ⊂ B sai vì A ∪ B chứa cả những phần tử thuộc A.
e) (A ∩ B) ⊂ A đúng.
Bài 6. Dùng kí hiệu ∀ hoặc ∃ để viết các mệnh đề sau:
a) Có một số nguyên không chia hết cho chính nó.
b) Mọi số thực cộng với 0 đều bằng chính nó.
Hướng dẫn giải
a) “ ”.
b) “ ”.
Bài 7. Cho A = {3; 5}, B = {3; x}, C = {5; y} và D = {m; n}. Tìm x, y, m, n để A = B = C và .
Hướng dẫn giải
+ Ta có: A = B = C khi mọi phần tử của A đều thuộc B và C.
Do đó: x = 5 và y = 3.
+ Để thì m và n phải khác 3 và 5.
Bài 8. Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) [– 3; 1) ∪ (0; 4];
b) (− 2; 15) ∪ (3; + ∞);
c) (− 12; 3] ∩ [− 1; 4];
d) \ (2; + ∞).
Hướng dẫn giải
a) [– 3; 1) ∪ (0; 4] = [– 3; 4]

b) (− 2; 15) ∪ (3; + ∞) = (− 2; +∞)
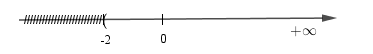
c) (− 12; 3] ∩ [− 1; 4] = [− 1; 3]

d) \ (2; + ∞) = (− ∞; 2]
![]()
Bài 9. Cho tam giác ABC. Xét các mệnh đề:
P: “Tam giác ABC có 3 cạnh bằng nhau”.
Q: “Tam giác ABC là tam giác đều”.
Hai mệnh đề P và Q có tương đương không? Nếu có, phát biểu bằng nhiều cách?
Hướng dẫn giải
+ P ⇒ Q: “Nếu tam giác ABC có 3 cạnh bằng nhau thì tam giác ABC là tam giác đều”. Đây là mệnh đề đúng.
+ Q ⇒ P: “Nếu tam giác ABC là tam giác đều thì tam giác ABC có 3 cạnh bằng nhau”. Đây là mệnh đề đúng.
Do đó: P và Q là hai mệnh đề tương đương.
Ta phát biểu mệnh đề P ⇔ Q như sau:
+ “Tam giác ABC có 3 cạnh bằng nhau tương đương với tam giác ABC là tam giác đều”.
+ “Tam giác ABC có 3 cạnh bằng nhau khi và chỉ khi tam giác ABC là tam giác đều”.
+ “Tam giác ABC có 3 cạnh bằng nhau là điều kiện cần và đủ để có tam giác ABC là tam giác đều”.
Bài 10. Hãy viết tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử.
a) A là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 20.
b) B là tập hợp các tỉnh thuộc vùng Bắc Trung Bộ.
Hướng dẫn giải
a) Các số tự nhiên chia hết cho 3 và nhỏ hơn 20 là: 0, 3, 6, 9, 12, 15, 18.
Ta viết tập hợp A bằng cách liệt kê các phần tử như sau:
A = {0; 3; 6; 9; 12; 15; 18}.
Tập hợp A có 7 phần tử, ta viết n(A) = 7.
Ngoài ra ta cũng có thể viết tập hợp A bằng cách chỉ ra tính chất đặc trưng là:
A = {x | x ⁝ 3; x < 20}.
b) Các tỉnh thuộc vùng Bắc Trung Bộ là: Thanh Hóa, Nghệ An, Hà Tĩnh, Quảng Bình, Quảng Trị.
Do đó: B = {Thanh Hóa; Nghệ An; Hà Tĩnh; Quảng Bình; Quảng Trị}.
Tập hợp B có 5 phần tử, ta viết n(B) = 5.
B2. Bài tập trắc nghiệm
Bài 1. Cho hai tập A = [–1 ; 3); B = [a; a + 3]. Với giá trị nào của a thì .
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: A
.
Bài 2. Cho A = {0; 1; 2; 3; 4}; B = {2; 3; 4; 5; 6}. Tìm tập
A. {5; 6};
B. {1; 2};
C. {2; 3; 4};
D. {0; 1; 5; 6}.
Hướng dẫn giải
Đáp án đúng là: D
Ta có tập hợp A\B là tập các phần tử thuộc tập A nhưng không thuộc tập B nên .
Tập hợp B\A là tập các phần tử thuộc tập B nhưng không thuộc tập A nên .
.
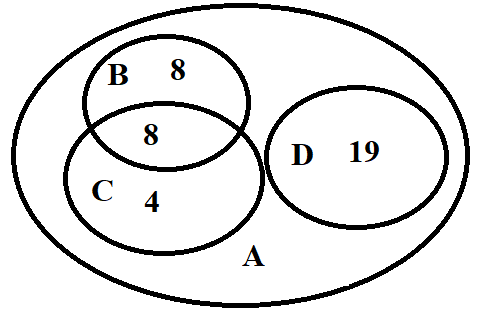
Bài 3. Một lớp học có 16 học sinh học giỏi môn Toán; 12 học sinh học giỏi môn Văn; 8 học sinh vừa học giỏi môn Toán và Văn; 19 học sinh không học giỏi cả hai môn Toán và Văn. Hỏi lớp học có bao nhiêu học sinh?
A. 31;
B. 54;
C. 39;
D. 47.
Hướng dẫn giải
Đáp án đúng là: C
Gọi A là tập hợp gồm các học sinh trong lớp; B là tập số học sinh giỏi Toán; C là tập số học sinh giỏi Văn; D là tập số học sinh không giỏi cả 2 môn Toán và Văn.
Khi đó n(B) = 16, n(C) = 12, n(B∩C) = 8, n(D) = 19.
Số học sinh trong lớp giỏi ít nhất một trong hai môn Toán hoặc Văn là:
n(B∪C) = n(B) + n(C) - n(B∩C) = 16 + 12 – 8 = 20.
Ta có A =
Số học sinh trong lớp là: n(A) = n(B∪C) + n(D) = 20 + 19 = 39 (học sinh).
Được thể hiện trong biểu đồ Ven như sau:
Bài 4. Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu a và b cùng chia hết cho c thì a + b chia hết cho c;
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau;
C. Nếu a chia hết cho 3 thì a chia hết cho 9;
D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5.
Hướng dẫn giải
Đáp án đúng là: C
- Mệnh đề đảo của A là: Nếu a + b chia hết cho c thì a và b cùng chia hết cho c.
Chọn a = 5, b = 2, c = 7 thì a + b = 5 + 2 = 7 chia hết cho c = 7. Nhưng 2 không chia hết cho 7 và 5 cũng không chia hết cho 7. Do đó mệnh đề đảo của A sai.
- Mệnh đề đảo của B là: Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.
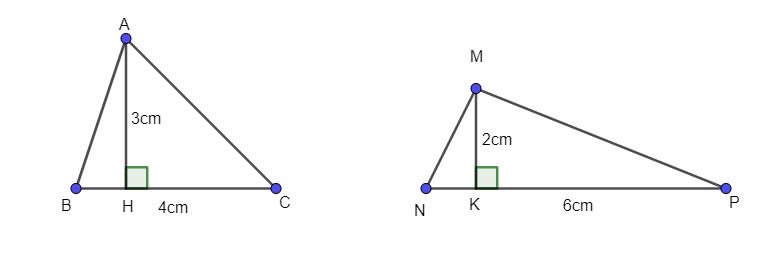
Hai tam giác ABC và MNP có cùng diện tích là 12 cm2. Tuy nhiên hai tam giác này không bằng nhau. Do đó mệnh đề đảo của B là sai.
- Mệnh đề đảo của C là: “Nếu a chia hết cho 9 thì a chia hết cho 3” là mệnh đề đúng.
- Mệnh đề đảo của D là: “Nếu số đó chia hết cho 5 thì số đó có chữ số tận cùng là 0”. Ví dụ số 25 chia hết cho 5 nhưng số này có tận cùng là 5 chứ không phải 0. Do đó mệnh đề đảo của D sai.
Bài 5. Cho mệnh đề A: “ ”. Mệnh đề phủ định của A là:
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: D
Phủ định của là
Phủ định của < là ≥
Do đó phủ định của mệnh đề A: “ ” là : “ ”.
Bài 6. Với giá trị thực nào của x mệnh đề chứa biến P(x): “2x2 – 1 < 0” là mệnh đề đúng
A. 0;
B. 5;
C. 1;
D. .
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
P(0) = 2.02 – 1 < 0 hay -1 < 0 (đúng). Do đó với x = 0 ta được một mệnh đề đúng.
P(5) = 2.52 – 1 < 0 hay 49 < 0 (sai). Do đó với x = 5 ta được một mệnh đề sai.
P(1) = 2.12 – 1 < 0 hay 1 < 0 (sai). Do đó với x = 1 ta được một mệnh đề sai.
P( ) = 2. – 1 < 0 hay (sai). Do đó với x = ta được một mệnh đề sai.
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Kết nối tri thức hay, chi tiết khác: