Tài liệu Bộ đề thi Toán lớp 12 giữa học kì 2 năm học 2024 - 2025 gồm 20 đề thi tổng hợp từ đề thi môn Toán 12 của các trường THPT trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi giữa học kì 2 Toán lớp 12. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi giữa kì 2 Toán 12 bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 1
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 1)
Câu 1. Nguyên hàm của hàm số 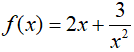 là:
là:
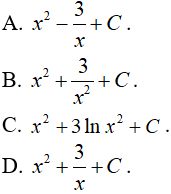
Câu 2. Tìm 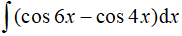 là:
là:
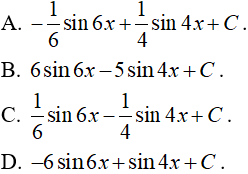
Câu 3. F(x) là nguyên hàm của hàm số y = sin4x.cosx. F(x) là hàm số nào sau đây?
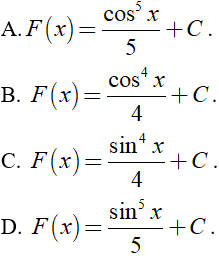
Câu 4. Để tính 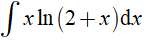 theo phương pháp tính nguyên hàm từng phần, ta đặt:
theo phương pháp tính nguyên hàm từng phần, ta đặt:
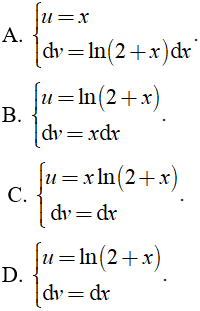
Câu 5. Kết quả của 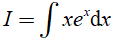 là:
là:
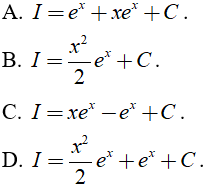
Câu 6. Giả sử 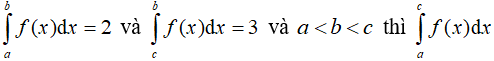 bằng bao nhiêu ?
bằng bao nhiêu ?
A. 5
B. 1
C. -1
D. -5
Câu 7. Cho hàm số f liên tục trên R và số thực dương a. Trong các đẳng thức sau, đẳng thức nào luôn đúng?
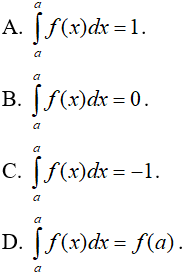
Câu 8. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [0;2]. Biết rằng F(0) = 0, F(2) = 1, G(0) = -2, G(2) = 1 và 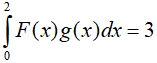 . Tích phân
. Tích phân 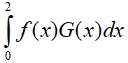 có giá trị bằng
có giá trị bằng
A. 3
B. 0
C. -2
D. - 4
Câu 9. Tính 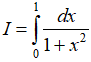
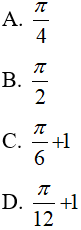
Câu 10. Tích phân 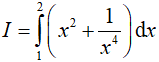 bằng
bằng
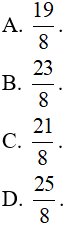
Câu 11. Tích phân 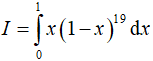 bằng
bằng
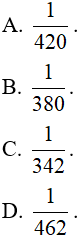
Câu 12. Biết rằng 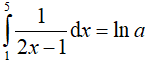 . Giá trị của a là :
. Giá trị của a là :
A. 9
B. 3
C. 27
D. 81
Câu 13. Tích phân 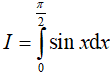 bằng:
bằng:
A. –1
B. 1
C. 2
D. 0
Câu 14. Cho 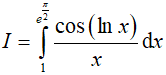 , ta tính được:
, ta tính được:
A. I = cos1
B. I = 1
C. I = sin1
D. Một kết quả khác
Câu 15. Tích phân 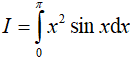 bằng :
bằng :
A. π2 - 4
B. π2 + 4
C. 2π2 - 3
D. 2π2 + 3
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 2
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 2)
Câu 1. Nguyên hàm của hàm số 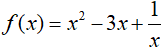 là:
là:
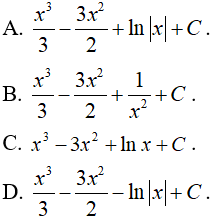
Câu 2. Tìm một nguyên hàm F(x) của hàm số 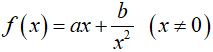 , biết rằng F(-1) = 1, F(1) = 4, ƒ(1) = 0. F(x) là biểu thức nào sau đây
, biết rằng F(-1) = 1, F(1) = 4, ƒ(1) = 0. F(x) là biểu thức nào sau đây
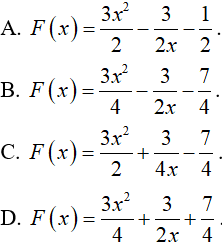
Câu 3. Nguyên hàm của hàm số 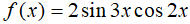 là :
là :
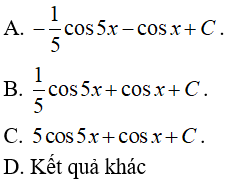
Câu 4. Gọi F(x) là một nguyên hàm của hàm số 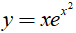 . Hàm số nào sau đây không phải là F(x):
. Hàm số nào sau đây không phải là F(x):
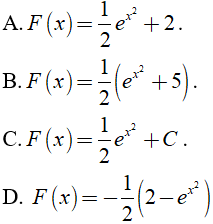
Câu 5. Tính nguyên hàm 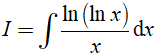 được kết quả nào sau đây?
được kết quả nào sau đây?
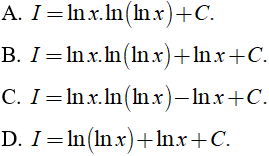
Câu 6. Cho 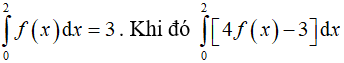 bằng
bằng
A. 2.
B. 4.
C. 6.
D. 8.
Câu 7. Cho hàm số f liên tục trên đoạn [a;b] có một nguyên hàm là hàm F trên đoạn [a;b]. Trong các phát biểu sau, phát biểu nào sai ?
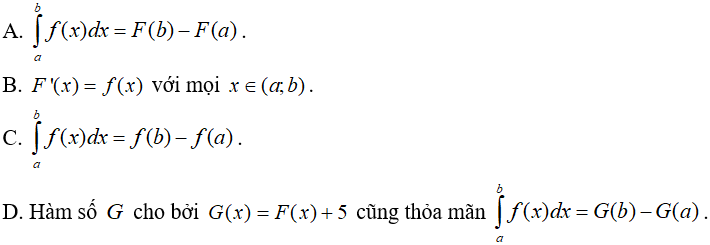
Câu 8. Tích phân 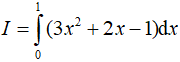 bằng
bằng
A. I = 1
B. I = 2
C. I = 3
D. I = -1
Câu 9. Tích phân 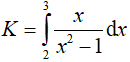 bằng
bằng
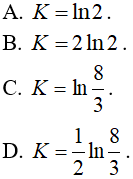
Câu 10. Biết 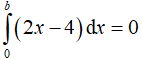 . Khi đó nhận giá trị bằng:
. Khi đó nhận giá trị bằng:
A. b = 0 hoặc b = 2.
B. b = 0 hoặc b = 4.
C. b = 1 hoặc b = 2.
D. b = 1 hoặc b = 4.
Câu 11. Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn 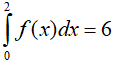 . Giá trị của tích phân
. Giá trị của tích phân 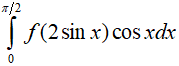 là
là
A. -6
B. 6
C. -3
D. 3
Câu 12. Tích phân 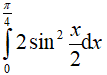 bằng:
bằng:
Câu 13. Tích phân 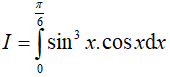 bằng:
bằng:
A. 6
B. 5
C. 4
D. 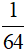
Câu 14. Tích phân 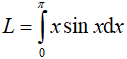 bằng:
bằng:
A. L = π B. L = -π
C. L = -2 D. L= 0
Câu 15. Để hàm số ƒ(x) = asinπx + b thỏa mãn 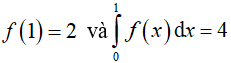 và thì a, b nhận giá trị
và thì a, b nhận giá trị
A. a = π, b = 0
B. a = π, b = 2
C. a = 2π, b = 2
D. a = 2π, b = 3
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 3
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 3)
Câu 1. Nguyên hàm của hàm số 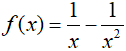 là :
là :
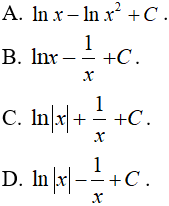
Câu 2. Nguyên hàm F(x) của hàm số 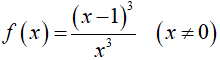 là
là
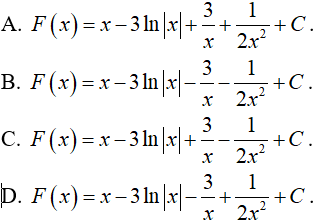
Câu 3. Tính 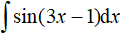 , kết quả là:
, kết quả là:
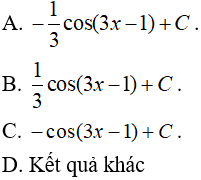
Câu 4. F(x) là một nguyên hàm của hàm số y = ℮sin x cos x.
Nếu F(π) = 5 thì 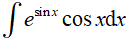 bằng:
bằng:
A. F(x) = ℮sin x + 4
B. F(x) = ℮sin x + C
C. F(x) = ℮cos x + 4
D. F(x) = ℮cos x + C
Câu 5. Hàm số ƒ(x) = (x - 1)℮x có một nguyên hàm F(x) là kết quả nào sau đây, biết nguyên hàm này bằng 1 khi x = 0?
A. F(x) = (x - 1)℮x
B. F(x) = (x - 2)℮x
C. F(x) = (x + 1)℮x + 1
D. F(x) = (x - 2)℮x + 3
Câu 6. Giả sử 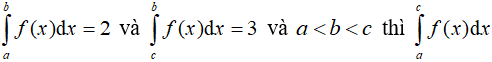 bằng bao nhiêu ?
bằng bao nhiêu ?
A. 5
B. 1
C. -1
D. -5
Câu 7. Cho hai hàm số f và g liên tục trên đoạn [a;b] và số thực k bất kỳ trong R. Trong các phát biểu sau, phát biểu nào sai?
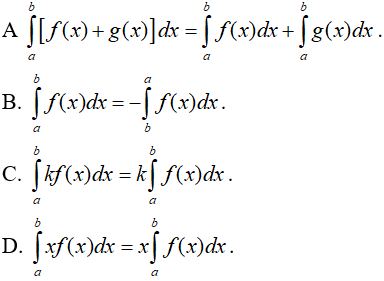
Câu 8. Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2]. Biết rằng 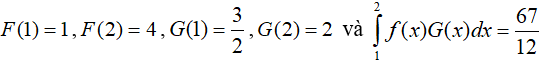 . Tích phân
. Tích phân 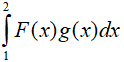 có giá trị bằng
có giá trị bằng
Câu 9. Tích phân 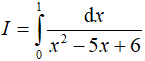 bằng
bằng
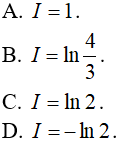
Câu 10. Tích phân 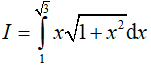 bằng
bằng
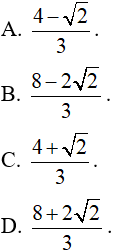
Câu 11. Tính tích phân sau 
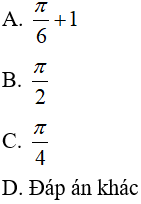
Câu 12. Tập hợp giá trị của m sao cho 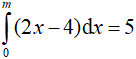 là
là
A. {5}
B. {5;-1}
C. {4}
D. {4;-1}
Câu 13. Tích phân 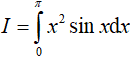 bằng :
bằng :
A. π2 - 4
B. π2 + 4
C. 2π2 - 3
D. 2π2 + 3
Câu 14. Đổi biến x = 2sint tích phân 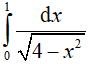 trở thành:
trở thành:
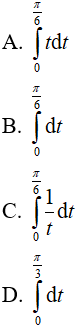
Câu 15. Tích phân 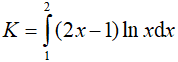 bằng:
bằng:
Đề thi Toán lớp 12 Giữa kì 2 năm 2022 (20 đề) - Đề 4
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 4)
Câu 1. Họ nguyên hàm của hàm số ƒ(x)=x2 - 2x + 1 là
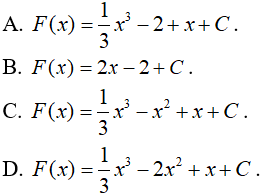
Câu 2. F(x) là một nguyên hàm của hàm số 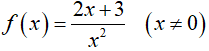 , biết rằng F(1) = 1. F(x). là biểu thức nào sau đây
, biết rằng F(1) = 1. F(x). là biểu thức nào sau đây
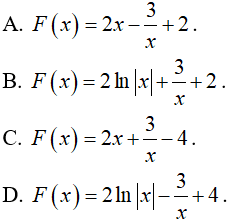
Câu 3. Nguyên hàm của hàm số ƒ(x) = √x + 2x là
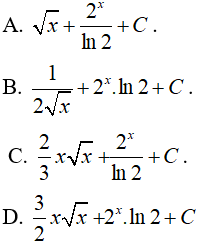
Câu 4. Một nguyên hàm của hàm số ƒ(x) = cos5xcosx là:
Câu 5. F(x) là một nguyên hàm của hàm số 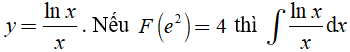 bằng:
bằng:
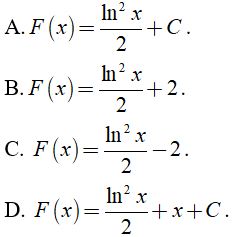
Câu 6. Một nguyên hàm của ƒ(x) = xlnx là kết quả nào sau đây, biết nguyên hàm này triệt tiêu khi x = 1 ?
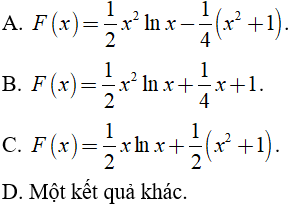
Câu 7. Xét hàm số f liên tục trên R và các số thực a, b, c tùy ý. Trong các khẳng định sau, khẳng định nào sai?
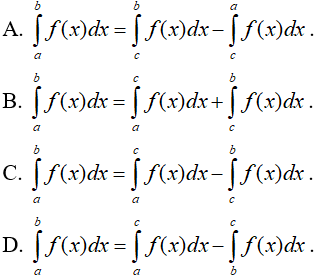
Câu 8. Giả sử 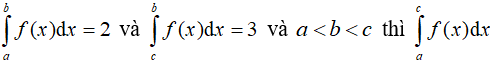 bằng bao nhiêu ?
bằng bao nhiêu ?
A. 5
B. 1
C. -1
D. -5
Câu 9. Tích phân 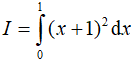 bằng
bằng
A. 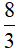
B. 2
C. 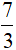
D. 4
Câu 10. Tích phân: 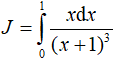 bằng
bằng
A. 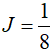
B. 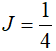
C. J = 2
D. J = 1
Câu 11. Giả sử 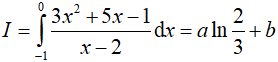 Khi đó giá trị a + 2b là
Khi đó giá trị a + 2b là
A. 30 B. 40 C. 50 D. 60
Câu 12. Tích phân I = 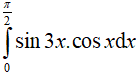 có giá trị là:
có giá trị là:
A. 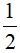
B. 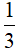
C. 1
D. 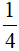
Câu 13. Tích phân 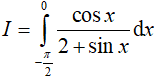 có giá trị là:
có giá trị là:
A. ln 3
B. 0
C. -ln 2
D. ln 2
Câu 14. Tích phân bằng:
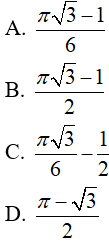
Câu 15. Tích phân 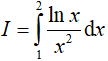 bằng:
bằng:
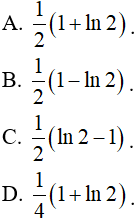
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 5
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 5)
Câu 1: Trong không gian Oxyz . Biết mặt cầu (S) nhận hai điểm A(4;2;0), B(-2;-4;3) làm hai đầu đường kính. Tính tâm I bán kính R của (S)
A. I (2;-2;3),= 9
B. ,
C. ,
D. ,
Câu 2: Tìm họ nguyên hàm của hàm số
A.
B.
C.
D.
Câu 3: Biết đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt có hoành độ lần lượt. Khi đó giá trị bằng:
A. 2 B. 5
C. 3 D. 1
Câu 4: Một người gửi tiết kiệm số tiền 18000000 đồng với lãi suất 6,0%/ năm( lãi suất không thay đổi trong suốt thời gian gửi). Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó rút được cả tiền gốc lẫn tiền lãi gần với con số nào sau đây?
A. 23000000 đồng B. 24088000 đồng C. 22725000 đồng D. 25533000 đồng
Câu 5: Với là số thực khác 0 tùy ý, bằng :
A. 2
B.
C.
D.
Câu 6: Số nghiệm nguyên nhỏ hơn 10 của bất phương trình là:
A. 10 B. 9
C. 8 D. 11
Câu 7: Cho hình trụ có diện tích xung quanh bằng và độ dài đường sinh bằng . Tính thể tích hình trụ đã cho
A. B.
C. D.
Câu 8: Đường tiệm cận ngang của đồ thị hàm số có phương trình là
A. B.
C. D.
Câu 9: Trong không gian , viết phương trình mặt phẳng đi qua điểm , song song với trục và vuông góc với mặt phẳng
A. B.
C. D.
Câu 10: Tìm mệnh đề sai trong các mệnh đề sau:
A.
B.
C.
D.
Câu 11: Trong không gian , viết phương trình mặt phẳng đi qua điểm , song song với trục và vuông góc với mặt phẳng
A.
B.
C.
D.
Câu 12: Cho hàm số liên tục trên . Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục và các đường thẳng ,là:
A.
B.
C.
D.
Câu 13: Cho , là các hàm số xác định và liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
A.
B.
C.
D.
Câu 14: Tích phân có giá trị bằng
A.
B. 2ln2
C.
D.
Câu 15: Trong không gian , cho hai điểm ,. Viết phương trình mặt phẳng trung trực của đoạn
A.
B.
C.
D.
Câu 16: Cho hàm số liên tục trên . Hãy chọn khẳng định đúng:
A. Hàm số luôn có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn
B. Hàm số không có giá trị lớn nhất trên đoạn
C. Hàm số không có giá trị nhỏ nhất trên đoạn
D. Hàm số luôn có cực đại và cực tiểu trên đoạn
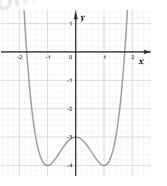
Câu 17: Cho hàm số có bảng biến thiên như sau
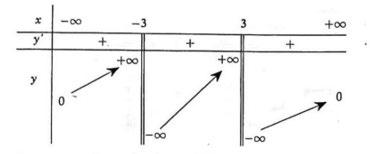
Số đường tiệm cận của đồ thị hàm số là:
A. 4 B. 2 C. 3 D. 1
Câu 18: Tính diện tích của hình phẳng giới hạn bởi các đường cong và
A. B.
C. D.
Câu 19: Trong không gian , cho tam giác có trọng tâm , biết , , . Tìm tọa độ điểm
A. B.
C. D.
Câu 20: Cho hai số thực và dương khác 1 với và . Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Câu 21: Với giá trị nào của thì hàm số xác định
A.
B.
C.
D.
Câu 22: Cho hàm số có đạo hàm trên đoạn , và . Khi đó bằng
A. 1 B. 10 C. -1 D. 11
Câu 23: Diện tích hình phẳng giới hạn bởi đồ thị hàm số và hai trục tọa độ là ( là hai số nguyên tố cùng nhau). Tính
A. B. C. D. 1
Câu 24: Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên tập xác định của nó?
A. 4 B. 3 C. 5 D. 2
Câu 25: Cho lăng trụ tam giác đều có tất cả các cạnh đều bằng . Thể tích của khối lăng trụ đã cho bằng
A. B.
C. D.
Câu 26: Tập nghiệm S của bất phương trình là:
A.
B.
C.
D.
Câu 27: Trong không gian. Biết mặt cầu đi qua gốc tọa độ và các điểm , , . Phương trình
A.
B.
C.
D.
Câu 28: Trong không gian, gọi lần lượt là hình chiếu vuông góc của điểm trên các trục . Viết phương trình mặt phẳng
A.
B.
C.
D.
Câu 29: Tính tích phân
A. B.
C. D.
Câu 30: Trong không gian , tìm hình chiếu của điểm trên mặt phẳng
A. B.
C. D.
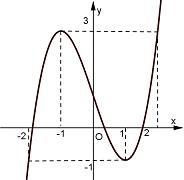
Câu 31: Cho hàm số có đồ thị như hình vẽ bên
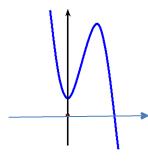
Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
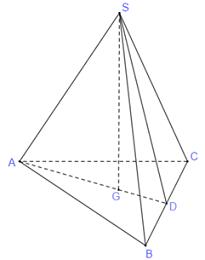
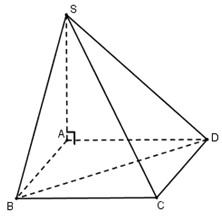
Câu 32: Cho hình chóp có đáy là tam giác đều cạnh 2, ,. Thể tích khối chóp bằng
A. B.
C. D.
Câu 33: Tích phân bằng
A. B. C. D.
Câu 34: Diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng bằng
A. B. C. D.
Câu 35: Cho hình nón bán kính đáy bằng 4 . Biết rằng khi cắt hình nón đã cho bởi mặt phẳng đi qua trục ta được thiết diện là một tam giác đều. Diện tích xung quanh của hình nón đã cho bằng
A. B. C. D.
Câu 36: Gọi và lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tính ?
A. B. C. D.
Câu 37: Giả sử là hàm số liên tục trên khoảng và là ba số bất kỳ trên khoảng . Khẳng định nào sau đây sai?
A. , B.
C. D.
Câu 38: Hàm số có
A. một cực đại và hai cực tiểu B. một cực tiểu và cực đại
C. một cực đại duy nhất D. một cực tiểu duy nhất
Câu 39: Cho đồ thị hàm số như hình vẽ.
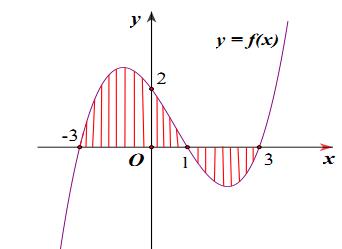
Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số và trục (phần gạch sọc) được tính bởi công thức
A.
B.
C.
D.
Câu 40: Cho hình lập phương có đường chéo bằng . Thể tích mặt cầu ngoại tiếp hình lập phương đó là
A. B.
C. D.
Câu 41: Trong không gian , cho mặt cầu Biết ba điểm nằm trên mặt cầu sao cho . Khi đó diện tích tam giác có giá trị lớn nhất bằng
A. B. C. 2 D. 4
Câu 42: Cho hai số dương thỏa mãn . Tính
A.
B.
C.
D.
Câu 43: Cho hàm số có đồ thị hàm số như hình vẽ. Hàm số đồng biến trên khoảng nào trong các khoảng sau đây
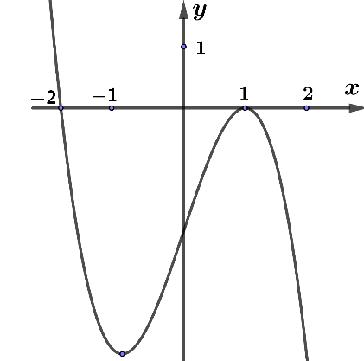
A. B. và
C. D.
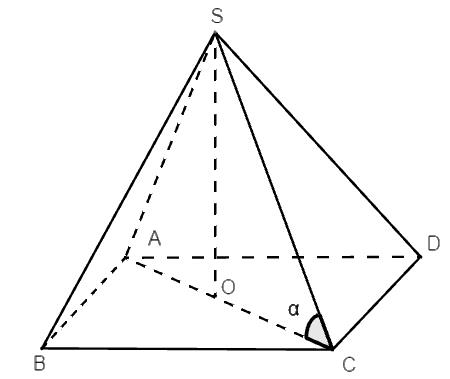
Câu 44: Cho hình chóp tứ giác đều có cạnh đáy bằng , cạnh bên hợp với mặt đáy một góc . Tính bán kính mặt cầu ngoại tiếp hình chóp
A. B.
C. D.
Câu 45: Trong mặt phẳng cho nửa đường tròn tâm . Parabol có đỉnh trùng với tâm (trục đối xứng là trục tung) cắt nửa đường tròn tại hai điểm như hình vẽ. Tính diện tích hình phẳng giới hạn bởi nửa đường tròn và Parabol ( phần gạch sọc)
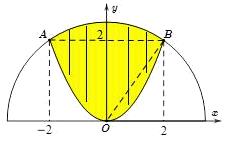
A.
B.
C.
D.
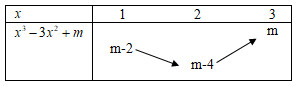
Câu 46: Cho hàm số . Có bao nhiêu số nguyên để
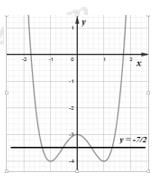
A. 4 B. 10 C. 6 D. 11
Câu 47: Biết là hai nghiệm của phương trình và với là hai số nguyên dương. Tính
A. B.
C. D.
Câu 48: Cho tích phân với là số thực, và là các số nguyên dương, đồng thời là phân số tối giản. Tính giá trị của biểu thức
A. B.
C. D.
Câu 49: Biết rằng hàm số liên tục trên thỏa ;. Tính
A. B.
C. D.
Câu 50: Trong không gian , cho mặt cầu có tâm là gốc tọa độ và bán kính bằng 1. Viết phương trình mặt phẳng đi qua điểm và tiếp xúc với mặt cầu
A.
B.
C.
D.
Lời giải chi tiết
|
1.B |
2.D |
3.B |
4.B |
5.C |
|
6.A |
7.A |
8.B |
9.A |
10.B |
|
11.C |
12.D |
13.D |
14.C |
15.A |
|
16.A |
17.C |
18.D |
19.B |
20A |
|
21.C |
22.C |
23.B |
24.C |
25.B |
|
26.C |
27.C |
28.B |
29.C |
30.A |
|
31.C |
32.A |
33.D |
24.A |
35.D |
|
36.D |
37.C |
38.A |
39.B |
40.D |
|
41.D |
42.B |
43.B |
44.A |
45.D |
|
46.D |
47.C |
48.A |
49.D |
50.B |
Câu 1(NB) – Mặt cầu
Phương pháp:
Sử dụng công thức tính vecto, công thức tính độ dài đoạn thẳng.
Cách giải:
Mặt cầu có tâm là trung điểm của AB ; bán kính
Chọn B
Câu 2(NB) – Nguyên hàm.
Phương pháp:
Sử dụng các công thức tính nguyên hàm.
Cách giải:
Ta có:
Chọn D
Câu 3(TH) – Tương giao đồ thị hàm số.
Phương pháp:
Tìm hoành độ giao điểm của hai đồ thị hàm số.
Áp dụng định lý Vi-et.
Cách giải:
Xét phương trình hoành độ giao điểm:
Phương trình trên có 2 nghiệm (Theo Vi-ét)
Câu 4(TH) – Cấp số cộng, cấp số nhân (lớp 11).
Phương pháp:
Áp dụng công thức tính cấp số nhân.
Cách giải:
Số tiền người đó nhận được: (triệu đồng)
Chọn B
Câu 5(NB) – Hàm logarit.
Phương pháp:
Sử dụng tính chất hàm logarit.
Cách giải:
Ta có:
Chọn C
Câu 6(TH) – Bất phương trình mũ.
Phương pháp
Đặt ẩn phụ, đưa về phương trình bậc 2 và giải tìm nghiệm.
Cách giải:
Đặt , ta được hay
Theo đề bài, nên
Chọn A
Câu 7(NB) – Mặt trụ.
Phương pháp:
Sử dụng các công thức tính diện tích xung quanh và thể tích hình trụ.
Cách giải:
-
-
Chọn A
Câu 8(TH) – Đường tiệm cận.
Phương pháp:
Tìm giới hạn của hàm số và kết luận.
Cách giải:
Vậy là TCN của đồ thị hàm số
Chọn B
Câu 9(TH) – Hệ tọa độ trong không gian.
Phương pháp:
Sử dụng công thức tính vecto trong không gian.
Cách giải:
Ta có:
Chọn A
Câu 10(NB) – Nguyên hàm.
Phương pháp:
Áp dụng công thức tính nguyên hàm.
Cách giải:
Ta thấy:
Chọn B
Câu 11(TH) - Đường thẳng và mặt phẳng trong không gian
Phương pháp:
Sử dụng công thức tính vecto có hướng.
Cách giải:
-
Vecto pháp tuyến của mặt phẳng là :
Mặt phẳng có và đi qua điểm
Chọn C
Câu 12(TH) - Ứng dụng của tích phân trong hình học.
Phương pháp:
Áp dụng công thức tính diện tích hình phẳng giới hạn.
Cách giải:
Công thức tính diện tích hình phẳng cần tìm là :
Chọn D
Câu 13(NB) – Nguyên hàm.
Phương pháp:
Áp dụng các tính chất của nguyên hàm.
Cách giải:
sai do không có tính chất này
Chọn D
Câu 14(TH) – Tích phân.
Phương pháp:
Sử dụng các công thức để tính tích phân.
Cách giải:
Ta có:
Theo công thức giải nhanh
Chọn C
Câu 15(TH) – Phương trình đường thẳng trong không gian.
Phương pháp:
Sử dụng công thức tính vecto trong không gian.
Cách giải:
Trung điểm của đoạn là
Ta có:
Mặt phẳng trung trực của đoạn có và đi qua điểm
Chọn A
Câu 16(NB) – Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Phương pháp:
Dựa vào dữ kiện đề bài.
Cách giải:
Chọn A
Câu 17(TH) – Đường tiệm cận.
Phương pháp:
Sử dụng các công thức tính giới hạn để suy ra tiệm cận của đồ thị hàm số.
Cách giải:
Ta có:
Vậy hàm số có 2 TCĐ là và
Lại có :
Vậy hàm số có 1 TCN là
Đồ thị hs có 3 đường tiện cận
Chọn C
Câu 18(TH) - Ứng dụng của tích phân.
Phương pháp:
Tìm hoành độ giao điểm của hai đồ thị hàm số.
Áp dụng công thức tính diện tích hình phẳng.
Cách giải:
- Xét pt hoành độ giao điểm:
hoặc
Diện tích của hình phẳng là:
Chọn D
Câu 19(NB) – Hệ tọa độ trong không gian.
Phương pháp:
Áp dụng công thức tính tọa độ điểm trong không gian.
Cách giải:
Tọa độ điểm C là
Chọn B
Câu 20(NB) – Hàm số mũ.
Phương pháp:
Sử dụng các tính chất của hàm mũ.
Cách giải:
;
Chọn A
Câu 21(NB) – Hàm số logarit.
Phương pháp:
Áp dụng tính chất hàm logarit.
Cách giải:
Hàm số xác định khi
và hay
Chọn C
Câu 22(NB) – Tích phân.
Phương pháp:
Sử dụng các tính chất của tích phân.
Cách giải:
- Theo bài ra, , mà nên
Chọn C
Câu 23: (TH) – Tích phân
Phương pháp:
Sử dụng công thức tính diện tích hình phẳng
Cách giải:
- Giao điểm của đồ thị hàm số với là
Diện tích S cần tìm :
- Nên
Chọn B
Câu 24: (TH) - Ứng dụng của đạo hàm
Phương pháp:
Ứng dụng của đạo hàm tìm khoảng đồng biến
Cách giải:
-
Hàm số đồng biến trên tập xác định (R) khi
Vậy có 5 giá trị của m thỏa mãn
Chọn C
Câu 25: (NB) – Khối đa diện
Phương pháp:
Áp dụng công thức tính thể tích
Cách giải:
- Thể tích khối lăng trụ tam giác đều :
Chọn B
Câu 26: (NB) – Hàm số logarit
Phương pháp:
Áp dụng tính chất của hàm số log
Cách giải:
- TXĐ :
BPT
Vậy tập nghiệm của BPT là
Chọn C
Câu 27: (TH) – Mặt cầu
Phương pháp:
Áp dụng hệ phương trình 4 ẩn đi qua 4 điểm
Cách giải:
- Gọi phương trình là:
Vì mặt cầu đi qua O nên
A nên
B nên
C nên
Chọn C
Câu 28: (VDT) – Phương trình mặt phẳng
Phương pháp:
Áp dụng công thức tích có hướng
Cách giải:
- Tọa độ các điểm ; ;
-
Vecto pháp tuyến của là
qua và có
Chọn B
Câu 29: (VDT) – Tích phân
Phương pháp:
Nguyên hàm từng phần
Cách giải:
Đặt
Chọn C
Câu 30: (NB) – Hệ tọa độ trong không gian
Phương pháp:
Tìm hình chiếu của điểm
Cách giải:
Gọi H là hình chiếu của trên
Chọn A
Câu 31: (VDT) – Khảo sát đồ thị hàm số
Phương pháp:
Dựa vào các dấu hiệu đồ thị để tìm ẩn
Cách giải:
- Vì đồ thị có dạng đi xuống
- Giao điểm của đồ thị với nằm phía trên trục hoành
- có 2 nghiệm phân biệt và nên
Mà
Chọn C
Câu 32: (TH): Khối đa diện
Phương pháp:
Áp dụng công thức tính thể tích khối đa diện
Cách giải:
- Thê tích khối chóp là:
Chọn B
Câu 33: (VDT) – Tích phân
Phương pháp:
Tích phân từng phần
Cách giải:
Đặt
Chọn D
Câu 34: (TH) - Ứng dụng của tích phân trong hình học
Phương pháp:
Áp dụng công thức tính diện tích hình phẳng
Cách giải:
Diện tích cần tìm:
Chọn A
Câu 35: (NB) – Hình nón
Phương pháp:
Sử dụng công thức tính diện tích xung quanh
Cách giải:
Vì thiết diện cắt qua trục là tam giác đều nên
Chọn D
Câu 36: (VDT) - Ứng dụng của đạo hàm khảo sát hàm số
Phương pháp:
Lập bảng biến thiên rồi tìm min, max
Cách giải:
,
; ;
Ta có BBT
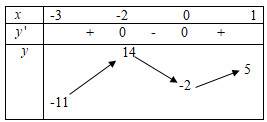
Vậy
Chọn D
Câu 37: (NB) – Tích phân
Phương pháp:
Sử dụng định nghĩa của tích phân
Cách giải:
chứ không thể bằng 1
Chọn C
Câu 38: (TH) - Ứng dụng đạo hàm khảo sát hàm số
Phương pháp:
Lập BBT rồi tìm các cực đại, cực tiểu
Cách giải:
; . Ta có BBT:

Dựa vào BBT hàm số có 1 cực đại và 2 cực tiểu
Chọn A
Câu 39: (TH): Tích phân
Phương pháp:
Sử dụng công thức tính diện tích hình phẳng
Cách giải:
-
Chọn B
Câu 40: (TH) – Mặt cầu
Phương pháp:
Sử dụng công thức tính diện tích mặt cầu
Cách giải:
Mặt cầu ngoại tiếp khối lập phương có tâm là trung điểm đường chéo, bán kính là
Diện tích mặt cầu là:
Chọn D
Câu 41: (VDT) - Mặt cầu
Phương pháp:
Sử dụng tính chất của cung tròn
Cách giải:
Mặt cầu có tâm và
Diện tích tam giác có giá trị lớn nhất khi nằm chính giữa cung . Mà nên là đường kính
Khi đó
Chọn D
Câu 42: (VDT) – Hàm số logarit
Phương pháp:
Sử dụng các công thức về hàm số log
Cách giải:
Đặt
Hệ pt trở thành hay và
Chọn B
Câu 43: (VDT) - Ứng dụng đạo hàm khảo sát hàm số
Phương pháp:
Tìm khoảng đồng biến, nghịch biến của hàm ẩn
Cách giải:
hoặc
Dựa vào đồ thị , ta thấy khi và . Vậy và
Ta có BBT

Dựa vào BBT, nhận thấy đồng biến trên và
Chọn B
Câu 44: (VDT) – Khối đa diện
Phương pháp:
Sử dụng công thức tính bán kính mặt cầu ngoại tiếp
Cách giải:
Gọi là hình chiếu của trên .
Mà
Bán kính mặt cầu ngoại tiếp:
Chọn A
Câu 45: (VDT) - Ứng dụng của tích phân
Phương pháp:
Sử dụng công thức tính diện tích hình phẳng
Cách giải:
Phương trình parabol là
Phương trình nửa đường tròn với dương :
Diện tích cần tìm là:
Chọn D
Câu 46: (VDC) – Giá trị lớn nhất và nhỏ nhất của hàm số
Phương pháp:
Biện luận tìm số nghiệm
Cách giải:
Ta có bảng giá trị:
+
+
( do )
+ (tm)
. Vậy có 11 số
Chọn D
Câu 47: (VDT) – Hàm số logarit
Phương pháp:
Áp dụng các định nghĩa về hàm số logarit
Cách giải:
và
Chọn C
Câu 48: (VDT) – Nguyên hàm
Phương pháp:
Nguyên hàm từng phần
Cách giải:
Đặt
. Vậy
Chọn A
Câu 49: (VDT) - Nguyên hàm
Phương pháp:
Nguyên hàm từng phần.
Cách giải:
Đặt
Chọn D
Câu 50: (VDT) – Phương trình mặt phẳng
Phương pháp:
Áp dụng tính chất của đường thẳng và mặt phẳng
Cách giải:
Vì mặt cầu tiếp xúc với tại nên .
đi qua và có
Chọn B
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 6
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 6)
Câu 1 . Trong không gian Oxyz, cho A(1;1;−1),B(−1;2;0),C(3;−1;−2). Giả sử M(a;b;c) thuộc mặt cầu (S):(x−1)2+y2+(z+1)2=861 sao cho P=2MA2−7MB2+4MC2 đạt giá trị nhỏ nhất. Giá trị T=|a|+|b|+|c| bằng
A. T=47. B. T=55
C. T=51 D. T=49.
Câu 2 Tìm nguyên hàm của hàm số f(x)=3x2+8sinx.
A. ∫f(x)dx=6x−8cosx+C.
B. ∫f(x)dx=6x+8cosx+C.
C. ∫f(x)dx=x3−8cosx+C.
D. ∫f(x)dx=x3+8cosx+C.
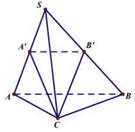
Câu 3 Cho tứ diện đều ABCD có cạnh bằng 4. Hình trụ (T) có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD. Diện tích xung quanh của (T) bằng:
A. 16√2π3. B. 8√2π.
C. 16√3π3. D. 8√3π.
Câu 4 Tập nghiệm của bất phương trình log131−2xx>0 có dạng (a;b). Tính T=3a−2b.
A. T=0. B. T=−1.
C. T=1. D. T=−23.
Câu 5 Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết AC=2a,BD=4a. Tính theo a khoảng cách giữa hai đường thẳng AD và SC.
A. a√152. B. 2a√55.
C. 2a3√153. D. 4a√136591.
Câu 6 Cho hàm số y=x3−3mx2+4m3. Với giá trị nào của m để hàm số có 2 điểm cực trị A,B sao cho AB=√20.
A. m=1;m=2
B. m=1
C. m=±1
D. m=±2
Câu 7 Biết rằng 2∫1x3−1x2+xdx=a+bln3+cln2 với a,b,c là các số hữu tỉ. Tính 2a+3b−4c.
A. −5 B. −19 C. 5 D. 19
Câu 8 . Tìm giá trị cực đại của hàm số y=−x3+3x2+1
A. 2 B. 5 C. 1 D. 0
Câu 9 . Cho hàm số y=f(x) liên tục trên R thỏa mãn 7∫0f(x)dx=10 và 3∫0f(x)dx=6. Tính I=3∫−2f|3−2x|dx.
A. 16 B. 3 C. 15 D. 8
Câu 10 . Cho bất phương trình log13(x2−2x+6)≤−2. Mệnh đề nào sau đây là đúng?
A. Tập nghiệm của bất phương trình là nửa khoảng.
B. Tập nghiệm của bất phương trình là một đoạn.
C. Tập nghiệm của bất phương trình là hợp của hai đoạn.
D. Tập nghiệm của bất phương trình là hợp của hai nửa khoảng.
Câu 11 . Ngày 20/01/2020, bà T gửi 100 triệu đồng vào ngân hàng theo hình thức lãi kép và lãi suất 0,7% mỗi tháng. Ngày 20/5/2020, lãi suất ngân hàng thay đổi với lãi suất mới là 0,75% mỗi tháng. Hỏi đến ngày 20/8/2020, số tiền bà T nhận về (cả vốn và lãi) gần nhất với số nào sau đây?
A. 105.160.500 đồng B. 105.212.812 đồng
C. 105.160.597 đồng D. 104.429.590 đồng
Câu 12 .Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng √2a. Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 43a3. Tính khoảng cách h từ B đến mặt phẳng (SCD).
A. h=23a B. h=43a
C. h=83a D. h=34a
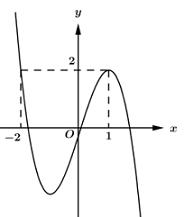
Câu 13 . Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(1−f(x))=2 là:
A. 2 B. 3 C. 5 D. 4
Câu 14 . Cho hàm số y=ax3+bx2+cx+d có đồ thị như hình bên dưới.
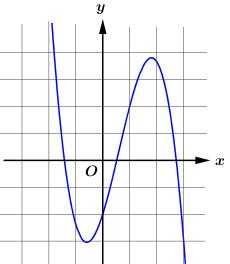
Trong các số a,b,c,d có bao nhiêu số dương?
A. 1 B. 0 C. 2 D. 3
Câu 15. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số y=2−x+3.
A. y=0 B. y=−2
C. x=3 D. x=−2
Câu 16 . Cho 1∫0dx√x+1+√x=23(√a−b) với a,b là các số nguyên dương. Giá trị của biểu thức T=a+b là:
A. 10 B. 7 C. 6 D. 8
Câu 17 . Tìm số nghiệm x thuộc [0;100] của phương trình sau :
2cosπx−1+12=cosπx+log4(3cosπx−1)
A. 51 B. 49 C. 50 D. 52
Câu 18 . Cho hàm số y=f(x). Đồ thị hàm số y=f′(x) như hình bên dưới. Hàm số g(x)=f(2+ex)nghịch biến trên khoảng nào trong các khoảng sau đây?
A. (−1;3) B. (−∞;0)
C. (0;+∞) D. (−2;1)
Câu 19. Cho hình chóp S.ABCD có đáy là hình chữ nhật, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, AB=a;AD=a√3. Thể tích khối chóp S.ABCD bằng
A. 3a22. B. a3
C. a36. D. a32
Câu 20 .Viết phương trình tiếp tuyến của đồ thị hàm số y=2x−1x−2, biết tiếp tuyến có hệ số góc k=−3.
A. y=−3x−14,y=−3x−2
B. y=−3x−4
C. y=−3x+4
D. y=−3x+14;y=−3x+2
Câu 21 . Cho ba điểm A(2;1;−1),B(−1;0;4),C(0;−2;−1). Mặt phẳng đi qua A và vuông góc với BC có phương trình là
A. x−2y−5z+5=0
B. x−2y−5z−5=0
C. 2x−y+5z+5=0
D. x−2y−5z=0
Câu 22 . Tính thể tích V của khối nón có độ dài đường sinh l=5a và bán kính của đường tròn đáy là r=3a
A. V=36πa3 B. V=12πa3
C. V=15πa3 D. V=45πa3
Câu 23 . Diện tích hình phẳng giới hạn bơi đường thẳng y=x+3 và parabol y=2x2−x−1 bằng:
A. 9 B. 136 C. 133 D. 92
Câu 24 . Họ nguyên hàm của hàm số f(x)=x2+2x là:
A. 13x3+2x+C B. 2x+2+C
C. x3+x2+C D. 13x3+x2+C
Câu 25 .Tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường thẳng 3x−2 và đồ thị hàm số y=x2 quanh quanh trục Ox.
A. 16 B. π6 C. 45 D. 4π5
Câu 26 . Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a và mặt phăng (DBC’) hợp với mặt đáy (ABCD) một góc 600. Tính theo a thể tích của khối lăng trụ ABCD.A’B’C’D’.
A. √6a32 B. √6a3 C. √6a36 D. √6a33
Câu 27 . Giá trị nhỏ nhất của hàm số f(x)=x4−12x2−4 trên đoạn [0;9] bằng:
A. −39 B. −40 C. −36 D. −4
Câu 28 . Làng gốm truyền thống Bát Tràng dự kiến làm một bức tranh gồm hình vuông cạnh 4(m), thiết kế có 4 đường parabol chung đỉnh tại tâm của hình vuông, tạo nên bốn cánh hoa (tham khảo hình vẽ). Phần diện tích cánh hoa (phần tô đậm) sẽ được tráng một lớp men đặc biệt. Chi phí tráng lớp men đó có đơn giá là 24 triệu đồng/m2. Tính số tiền phải trả để tráng men cho 4 cánh hoa.
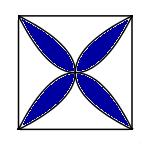
A. 132 triệu
B. 96 triệu
C. 32 triệu
D. 128 triệu
Câu 29 . Có bao nhiêu giá trị nguyên dương của m không vượt quá 2021 để phương trình 4x−1−m.2x−2+1=0 có nghiệm?
A. 2019 B. 2018 C. 2021 D. 2017
Câu 30 . Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn x<y và 4x+4y=32y−32x+48.
A. 5 B. 4 C. 2 D. 1
Câu 31. Trong không gian Oxyz, cho mặt phẳng (P):2x−y+2z+1=0 và hai điểm A(1;0;−2),B(−1;−1;3). Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình là
A. 3x+14y+4z−5=0.
B. 2x−y+2z−2=0.
C. 2x−y+2z+2=0.
D. 3x+14y+4z+5=0.
Câu 32 . Trong không gian Oxyz, cho hai điểm A(1;1;2),B(2;0;1). Mặt phẳng đi qua A và vuông góc với đường thẳng AB có phương trình là:
A. x+y−z=0.
B. x−y−z−2=0.
C. x+y+z−4=0.
D. x−y−z+2=0.
Câu 33 . Nghiệm của phương trình 3x−1=9 là
A. x=−2. B. x=3.
C. x=2. D. x=−3.
Câu 34 . Cho hình chóp S.ABC có đáy là tam giác cân tại A, mặt bên (SBC) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi (α) là mặt phẳng đi qua điểm B và vuông góc với SC, chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
A. 12 B. 13 C. 23 D. 14
Câu 35 . Trong một lô hàng có 12 sản phẩm khác nhau, trong đó có đúng 2 phế phẩm. Lấy ngẫu nhiên 6 sản phẩm từ lô hàng đó. Hãy tính xác suất để trong 6 sản phẩm được lấy ra có không quá một phế phẩm?
A. P=1721 B. P=2224
C. P=2150 D. P=1722
Câu 36 . Trong không gian Oxyz, cho đường thẳng d:x−34=y+1−2=z+23. Vectơ nào dưới đây là một vectơ chỉ phương của d?
A. →u3=(3;−1;−2).
B. →u4=(4;2;3).
C. →u2=(4;−2;3).
D. →u1=(3;1;2).
Câu 37. Họ nguyên hàm của hàm sốy=xsinx là
A. −xcosx−sinx+C
B. xcosx−sin2x+C
C. −xcosx+sinx+C
D. xcosx−sinx+C
Câu 38 . Nghiệm của phương trình sinx=1 là:
A. x=−π2+k2π B. x=π2+kπ
C. x=kπ D. x=π2+k2π
Câu 39 . Viết phương trình mặt phẳng vuông góc với (P):x−z+y=0 và chứa giao tuyến của hai mặt phẳng (Q):2x+2y−z+1=0 và (R):x+2y−2z+2=0.
A. x+z−1=0
B. x+y−z−1=0
C. x+z=0
D. x+z+1=0
Câu 40 . Trong không gian Oxyz, mặt phẳng (P) chứa hai đường thẳng d1:x−22=y+3−1=z−5−3 và d2:x+1−2=y+31=z−23. Khi đó phương trình mặt phẳng (P) là:
A. x−5y−z+18=0
B. x−5y+z−22=0
C. x+5y−z+18=0
D. x+3y−z+12=0
Câu 41 . Cho 2 đường thẳng song song d1,d2. Trên d1 có 6 điểm phân biệt được tô màu đỏ. Trên d2 có 4 điểm phân biệt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên 1 tam giác, khi đó xác suất để thu được tam giác có 2 đỉnh màu đỏ là:
A. 59. B. 532. C. 58. D. 57.
Câu 42 . Có bao nhiêu giá trị nguyên của m để hàm số y=mx+4x+m nghịch biến trên khoảng (−1;1)?
A. 4 B. 2 C. 5 D. 0
Câu 43 . Cho một khối lập phương biết rằng khi tăng độ dài cạnh của khối lập phương thêm 2cm thì thể tích của nó tăng thêm 98cm3. Hỏi cạnh của khối lập phương đã cho bằng:
A. 3cm B. 4cm C. 6cm D. 5cm
Câu 44 . Cho số tự nhiên n thỏa mãn C0n+C1n+C2n=11. Số hạng chứa x7 trong khai triển của (x3−1x2)n bằng:
A. −4 B. (9{x^2} C. −4x7 D. −12x7
Câu 45 .Trong không gian Oxyz phương trình đường thẳng đi qua hai điểm A(−3;1;2), B(1;−1;0) có dạng:
A. x+32=y−11=z−2−1
B. x−1−2=y+1−1=z1
C. x−12=y+1−1=z−1
D. x+32=y−1−1=z−2−1
Câu 46 . Cho hàm số f(x)=ax3+bx2+cx+d có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số g(x)=(x2−3x+2)√x−1x[f2(x)−f(x)] có bao nhiêu tiệm cận đứng?
A. 4 B. 3 C. 5 D. 2
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho A(−3;0;0),B(0;0;3),C(0;−3;0). Điểm M(a;b;c) nằm trên mặt phẳng Oxy sao cho MA2+MB2−MC2 nhỏ nhất. Tính a2+b2−c2.
A. 18 B. 0 C. 9 D. -9
Câu 48 . Tìm khoảng đồng biến của hàm số y=−x3+3x2−1.
A. (0;2). B. (0;3).
C. (−1;3). D. (−2;0).
Câu 49 . Trong không gian Oxyz, cho A(0;0;2),B(1;1;0) và mặt cầu (S):x2+y2+(z−1)2=14. Xét điểm M thay đổi thuộc (S). Giá trị nhỏ nhất của biểu thức MA2+2MB2 bằng:
A. 12 B. 34 C. 214 D. 194
Câu 50 . Hàm số y=2x3−3(m+1)x2+6mx+1 nghịch biến trên khoảng (1;3) khi và chỉ khi:
A. m≥1 B. 1<m<3 C. m>3 D. m≥3
Lời giải chi tiết
| 1.A | 2.C | 3.A | 4.D | 5.D |
| 6.C | 7.D | 8.B | 9.D | 10.D |
| 11.C | 12.B | 13.D | 14.C | 15.A |
| 16.A | 17.A | 18.B | 19.D | 20.D |
| 21.B | 22.B | 23.A | 24.A | 25.D |
| 26.A | 27.B | 28.D | 29.B | 30.D |
| 31.D | 32.D | 33.B | 34.A | 35.D |
| 36.C | 37.C | 38.D | 39.A | 40.C |
| 41.C | 42.B | 43.A | 44.C | 45.C |
| 46.B | 47.A | 48.A | 49.D | 50.D |
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 7
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 7)
Câu 1. Trong không gian , cho mặt cầu : và mặt phẳng với m là tham số. Gọi T là tập tất cả các giá trị thực của tham số m để mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn có chu vi bằng . Tổng giá trị của tất cả các phần tử thuộc T bằng
A. 4 B. 24 C. -20 D. -16
Câu 2. Đường thẳng là tiệm cận đứng của đồ thị hàm số nào dưới đây?
A. B.
C. D.
Câu 3. Hàm số có đạo hàm là
A.
B.
C.
D.
Câu 4. Một lớp học có 38 học sinh. Hỏi có bao nhiêu cách chọn ngẫu nhiên hai bạn học sinh trong lớp?
A. 406 B. 703
C. 360 D. 38
Câu 5. Cho hàm số . Tính giá trị biểu thức .
A. B.
C. C.
Câu 6. Đồ thị trong hình bên là của hàm số
S là diện tích hình phẳng (phần tô đậm trong hình) là
A.
B.
C.
D.
Câu 7. Số nghiệm nguyên của bất phương trình là
A. 6 B. 7 C. 8 D. 9
Câu 8. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng để hàm số đồng biến trên khoảng ?
A. 2021 B. 2020
C. 2018 D. 2019
Câu 9. Trong không gian , cho điểm và mặt phẳng . Mặt phẳng đi qua A và song song với mặt phẳng có phương trình là
A.
B.
C.
D.
Câu 10. Cho tứ diện ABCD, trên các cạnh BC, BD, AC lần lượt lấy các điểm M, N, P sao cho . Mặt phẳng chia khối tứ diện ABCD thành hai khối đa diện có thể tích là , trong đó khối đa diện chứa cạnh CD có thể tích là . Tính tie số .
A. B.
C. D.
Câu 11. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ tam giác đều có tất cả các cạnh bằng a
A. B.
C. D.
Câu 12. Hình lập phương có bao nhiêu mặt phẳng đối xứng?
A. 6 B. 7 C. 8 D. 9
Câu 13. Cho hàm số có đồ thị như hình vẽ
Số nghiệm của phương trình là
A. 3 B. 1 C. 2 D. 0
Câu 14. Cho hàm số biết . liên tục trên và . Tính .
A. 9 B. 10 C. 8 D. 7
Câu 15. Cho hàm số có đồ thị và đường thẳng . Đường thẳng cắt đồ thị tại 3 điểm phân biệt có hoành độ . Tìm giá trị lớn nhất của biểu thức .
A.
B.
C.
D.
Câu 16. Cho hai số thực x, y thỏa mãn : . Tìm giá trị nhỏ nhất của biểu thức
A. 4 B. -4 C. D.
Câu 17. Trong không gian , cho ba điểm , , . Mặt phẳng đi qua điểm nào sau đây?
A. B.
C. D.
Câu 18. Biết đồ thị hàm số đối xứng với đồ thị hàm số . Qua điểm . Tính
A. -2020 B. 2014
C. -2014 D. 2020
Câu 19. Cho hàm số có đồ thị (C). có bao nhiêu tiếp tuyến của (C) song song với đường thẳng ?
A. 3 B. 1 C. 0 D. 2
Câu 20. Trong không gian , cho mặt cầu . Bán kính R của mặt cầu bằng
A. B.
C. D.
Câu 21. Cho cấp số cộng biết . Công sai d của cấp số cộng là
A. B.
C. D.
Câu 22. Tính chiều cao của khối lăng trụ tam giác đều biết thể tích bằng , cạnh đáy bằng a.
A. B. C. D.
Câu 23. Một khối nón có thể tích bằng . Tính bán kính R đáy khối nón khi diện tích xung quanh nhỏ nhất.
A. B.
C. D.
Câu 24. Gọi m là giá trị nhỏ nhất của hàm số trên khoảng . Tìm m?
A. B.
C. D.
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, AC=a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA=a. Tính thể tích V của khối chóp S.ABCD.
A. B.
C. D.
Câu 26. Cho hàm số có đạo hàm trên thỏa mãn và đồ thị hàm số có dạng như hình dưới.
Hàm số đạt cực đại tại điểm nào?
A. B.
C. D.
Câu 27. Trong không gian , cho hai điểm , . Vectơ có tọa độ là
A. B.
C. D.
Câu 28. Cho khối chóp S.ABC, mặt bên SBC là tam giác vuông cân tại S có BC=2a, cạnh và tạo với mặt phẳng một góc . Tính thể tích của khối chóp S.ABC.
A. B.
C. D.
Câu 29. Tập nghiệm của phương trình là
A. B.
C. D.
Câu 30. Cho hàm số có đồ thị như hình vẽ
Giá trị cực đại của hàm số bằng
A. -2 B. 0 C. -1 D. 1
Câu 31. Cho hình nón có độ dài đường sinh , bán kính đáy . Diện tích xung quanh hình nón bằng
A. B.
C. D.
Câu 32. Trong không gian Oxyz, cho mặt phẳng . Một vectơ pháp tuyến của có tọa độ là
A. B.
C. D.
Câu 33. Cho hình trụ có trục , chiều cao bằng a. Trên hai đường tròn đáy và lần lượt lấy hai điểm A, B sao cho khoảng cách giữa hai đường thẳng AB và OO’ bằng . Góc giữa hai đường thẳng AB và OO’ bằng . Tính thể tích của khối trụ đã cho.
A. B.
C. D.
Câu 34. Cho hình hộp có đáy là hình chữ nhật với . Hình chiếu vuông góc của lên trùng với giao điểm của AC và BD. Tính khoảng cách từ B’ đến mặt phẳng .
A. B.
C. D.
Câu 35. Cho hàm số xác định và có đạo hàm cấp một và cấp hai trên khoảng và . Khẳng định nào sau đây sai?
A. Hàm số đạt cực đại tại thì .
B. và thì là điểm cực tiểu của hàm số.
C. và thì không là điểm cực trị của hàm số.
D. và thì là điểm cực trị của hàm số.
Câu 36. Tìm hệ số của số hạng chứa trong khai triển nhị thức Newton của biết rằng: (n nguyên dương).
A. 13440 B. -13440
C. 210 D. -120
Câu 37. Cho hàm số đồng biến và có đạo hàm cấp hai trên đoạn và thỏa mãn với . Biết , tính tích phân bằng
A. B.
C. D.
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và . Biết . Tính góc giữa SC và mặt phẳng .
A. B. C. D.
Câu 39. Trong không gian Oxyz cho 3 điểm và mặt phẳng . Gọi là điểm thuộc mặt phẳng (P) sao cho biểu thức đạt giá trị nhỏ nhất. Tính giá trị của biểu thức .
A. B.
C. D.
Câu 40. Tổng các nghiệm của phương trình trên đoạn bằng
A. B.
C. D.
Câu 41. Tìm tập xác định D của hàm số .
A. B.
C. D.
Câu 42. Gọi là một nguyên hàm của hàm số . Tìm khẳng định đúng.
A.
B.
C.
D.
Câu 43. Cho hình hộp chữ nhật có đáy là hình vuông cạnh a và . Thể tích khối tứ diện .
A. B. C. D.
Câu 44. Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình có 3 nghiệm phân biệt là . Tính .
A. 0 B. C. -2 D.
Câu 45. Nếu là một nguyên hàm của hàm số trên khoảng thì có giá trị bằng
A. B. 0 C. 2 D. 4
Câu 46. Cho là các hàm số liên tục trên và thỏa mãn , . Tích phân bằng
A. B.
C. D.
Câu 47. Một bình cắm hoa dạng khối tròn xoay, biết đáy bình và miệng bình có đường kính lần lượt là và . Mặt xung quanh của bình là một phần của mặt tròn xoay có đường sinh là đồ thị hàm số . Tính thể tích của bình cắm hoa đó.
A. B.
C. D.
Câu 48. Trong không gian Oxyz, cho hai điểm . Phương trình mặt cầu đường kính AB là
A.
B.
C.
D.
Câu 49. Đặt . Khi đó bằng
A. B.
C. D.
Câu 50. Tính thể tích V của khối trụ có bán kính đáy bằng 6 và chiều cao bằng 3.
A. B.
C. D.
Lời giải chi tiết
|
1.D |
2.D |
3.C |
4.B |
5.C |
|
6.D |
7.B |
8.D |
9.B |
10.A |
|
11.A |
12.D |
13.A |
14.B |
15.A |
|
16.C |
17.A |
18.C |
19.D |
20.A |
|
21.C |
22.D |
23.A |
24.B |
25.D |
|
26.C |
27.A |
28.D |
29.B |
30.C |
|
31.C |
32.C |
33.D |
34.D |
35.C |
|
36.A |
37.B |
38.A |
39.B |
40.B |
|
41.B |
42.C |
43.D |
44.B |
45.C |
|
46.A |
47.D |
48.A |
49.A |
50.B |
Câu 1(TH) – Hệ tọa độ trong không gian.
Phương pháp:
Tìm tâm I và bán kính mặt cầu (S).
Tìm khoảng cách từ I xuống mặt phẳng (P).
Áp dụng định lý Pytago để tìm m.
Cách giải:
Mặt cầu (S): có tâm và bán kính
Ta có mặt phẳng (P):
Mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn có chu vi bằng .
Ta có
Chọn D.
Câu 2(NB) – Đường tiệm cận.
Phương pháp:
Tìm giới hạn của các hàm số.
Cách giải:
Ta thấy là đường tiệm cận đứng của đồ thị hàm số
Chọn D.
Câu 3(NB) – Đạo hàm của hàm số.
Phương pháp:
Áp dụng công thức tính đạo hàm của hàm số mũ.
Cách giải:
Ta có
Chọn C.
Câu 4(NB) – Xác suất, chỉnh hợp, tổ hợp.
Phương pháp:
Áp dụng công thức tính tổ hợp.
Cách giải:
Chọn 2 bạn trong 38 học sinh thì có
Chọn B.
Câu 5(TH) – Đạo hàm của hàm số.
Phương pháp:
Tìm đạo hàm của hàm số.
Cách giải:
Ta có
Khi đó
Chọn C.
Câu 6(TH) - Ứng dụng của nguyên hàm, tích phân.
Phương pháp:
Áp dụng công thức tính diện tích hình phẳng.
Cách giải:
Ta có diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành là:
Chọn D.
Câu 7(NB) – Bất phương trình logarit.
Phương pháp:
Áp dụng các tính chất của hàm logarit.
Cách giải:
Ta có ĐKXĐ:
Khi đó có 7 giá trị thỏa mãn.
Chọn B.
Câu 8(VD) – Sự đồng biến và nghịch biến của hàm số.
Phương pháp:
Tìm đạo hàm của hàm số. Tìm nghiệm phương trình .
Cách giải:
Ta có hàm số có:
Bảng biến thiên:

Hàm số đồng biến trên khoảng khi có 2019 giá trị nguyên của m thỏa mãn bài toán.
Chọn D.
Câu 9(TH) – Phương trình mặt phảng.
Phương pháp:
Áp dụng tính chất của hai mặt phẳng song song.
Cách giải:
Mặt phẳng (Q) song song với mặt phẳng (P):
Nên mặt phẳng (Q) có dạng , đí qua
Nên
Mặt phăng(Q) có dạng
Chọn B.
Câu 10(VD) – Tỉ số thể tích.
Phương pháp:
Chia khối đa diện
Áp dụng định lý Menelaus.
Áp dụng tính chất về tỉ số thể tích.
Cách giải:
Trong gọi
Trong gọi
Khi đó thiết diện của hình chóp khi cắt bởi mặt phẳng là tứ giác MNQP.
Áp dụng định lí Menelaus trong tam giác BCD có:
Áp dụng định lý Menelaus trong tam giác ACD có:
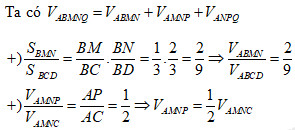
Nên
Gọi là thể tích phần còn lại
Chọn A.
Câu 11(TH) – Mặt cầu.
Phương pháp:
Tìm tâm của mặt cầu.
Áp dụng công thức tính diện tích mặt cầu.
Cách giải:
Gọi hình lăng trụ tam giác đều đó là
Gọi O là tâm tam giác ABC; O’ là tâm tam giác
Gọi I là trung điểm của OO’
Khi đó ;
Khi đó bán kính mặt cầu ngoai tiếp hình lăng trụ là
Nên diện tích mặt cầu đó là
Chọn A.
Câu 12(NB) – Khối đa diện.
Phương pháp:
Áp dụng các tính chất của hình lập phương để chỉ ra mặt phẳng đối xứng.
Cách giải:
Hình lập phương là hình có 12 cạnh bằng nhau nên có
3 mặt phẳng đối xứng đi qua trung điểm 4 cạnh song song với nhau chia hình lập phương thành 2 khối hộp chữ nhật.
6 mặt còn lại chia khối lập phương thành 2 khối lăng trụ tam giác bằng nhau.
Vậy tổng có 9 mặt phẳng đối xứng.
Chọn D.
Câu 13(TH) – Tương giao đồ thị hàm số và biện luận nghiệm của phương trình.
Phương pháp:
Dựa vào đồ thị hàm số để xác định nghiệm của phương trình.
Cách giải:
Ta có
Số nghiệm của phương trình trên là số giao điểm của đồ thị hàm số và đường thẳng
Dựa vào đồ thị hàm số ta thấy 2 đồ thị trên giao nhau tại 3 điểm phân biệt
Vậy phương trình có 3 nghiệm phân biệt.
Chọn A.
Câu 14(TH) – Nguyên hàm, tích phân.
Phương pháp:
Áp dụng tính chất của nguyên hàm, tích phân.
Cách giải:
Ta có
mà
Chọn B.
Câu 15(VD) – Giá trị lớn nhất và nhỏ nhất của hàm số.
Phương pháp:
Tìm giao điểm của hai đồ thị hàm số.
Tìm nghiệm của phương trình và tìm quan hệ của các nghiệm.
Cách giải:
Hoành độ giao điểm của đồ thị hàm số và đường thẳng là nghiệm của phương trình
Từ (1) có
Khi đó
Nên
Chọn A.
Câu 16(VD) – Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Phương pháp:
Áp dụng tính chất hàm logarit.
Tìm mối quan hệ của x và y.
Cách giải:
Ta có
Khi đó
Xét
Khi đó
Chọn C.
Câu 17(TH) – Hệ tọa độ trong không gian.
Phương pháp:
Tìm các vecto của mặt phẳng.
Áp dụng công thức tính vecto có hướng.
Cách giải:
Ta có
Nên
Do đó vecto pháp tuyến của mặt phẳng (ABC) là
Khi đó phương trình mặt phẳng (ABC) là
Nên thuộc mặt phẳng trên.
Chọn A.
Câu 18(TH)
Phương pháp:
Áp dụng tính chất đối xứng.
Cách giải:
Đồ thị hàm số đối xứng với đồ thị hàm số qua điểm
Gọi là điểm thuộc đồ thị hàm số và điểm đối xứng của nó qua là
Nên
Khi đó
Chọn C.
Câu 19(TH) – Phương trình tiêp tuyến.
Phương pháp:
Tìm đạo hàm của hàm số.
Áp dụng tính chất song song.
Cách giải:
Ta có
Nên hệ số góc của tiếp tuyến là
Tiếp tuyến song song với đường thẳngnên ta có
Chọn D.
Câu 20(NB) – Mặt cầu.
Phương pháp:
Tìm tâm của mặt cầu.
Áp dụng công thức tính bán kính mặt cầu.
Cách giải:
Ta cócó tâm là
Khi đó bán kính
Chọn A.
Câu 21(NB) – Cấp số cộng.
Phương pháp:
Áp dụng công thức của cấp số cộng.
Cách giải:
Ta có
Chọn C.
Câu 22(NB) – Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích khối lăng trụ tam giác đều.
Cách giải:
Khối lăng trụ tam giác đều là khối lăng trụ có đáy là tam giác đều cạnh a
Nên
Chọn D.
Câu 23(TH) – Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích khối nón.
Cách giải:
Khối nón có thể tích bằng , bán kính đáy R
Nên
Diện tích xung quanh hình nón là
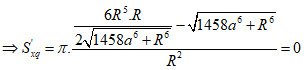
Chọn A.
Câu 24(TH) – Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Phương pháp:
Tìm đạo hàm của hàm số.
Xác định tính đơn điệu của hàm số trên khoảng đã cho
Cách giải:
Ta có
Bảng biến thiên trên khoảng
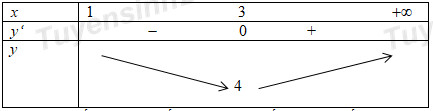
Dựa vào bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số là
Chọn B.
Câu 25(TH) – Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích khối chóp.
Cách giải:
Vì ABCD là hình thoi cạnh a và nên tam giác ABC là tam giác đều cạnh a.
Khi đó thể tích khối chóp là
Chọn D.
Câu 26(VD) – Tương giao đồ thị hàm số và tìm nghiệm của phương trình.
Phương pháp:
Tìm đạo hàm của hàm số .
Dựa vào đồ thị hàm số để biện luận.
Cách giải:
Ta có
Bảng biến thiên của hàm số

Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại điểm
Chọn C.
Câu 27(NB) – Hệ tọa độ trong không gian.
Phương pháp:
Áp dụng công thức tính vecto trong không gian.
Cách giải:
Ta có
Chọn A.
Câu 28(TH) - Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích khối chóp.
Cách giải:
Gọi h là chiều cao hạ từ A xuống mặt phẳng
Ta có
Tam giác SBC vuông cân tại S có
Khi đó thể tích khối chóp S.ABC là
Chọn D.
Câu 29(NB) – Phương trình hàm mũ.
Phương pháp:
Đưa 2 vế của phương trình về dạng cùng cơ số.
Cách giải:
Ta có
Chọn B.
Câu 30(NB) – Cực trị của hàm số.
Phương pháp:
Dựa vào đồ thị hàm số để xác định.
Cách giải:
Dưạ vào đồ thị hàm số ta thấy giá trị cực đại của hàm số là
Chọn C.
Câu 31(TH) – Mặt nón.
Phương pháp:
Áp dụng công thức tính diện tích xung quanh mặt nón.
Cách giải:
Hình nón có đường sinh , bán kính đáy thì diện tích xung quanh là
Chọn C.
Câu 32(NB) – Phương trình mặt phẳng.
Phương pháp:
Mặt phẳng có dạng là vecto pháp tuyến của nó.
Cách giải:
Mặt phẳng có vecto pháp tuyến là
Chọn C.
Câu 33(VD) – Mặt trụ.
Phơng pháp:
Áp dụng các công thức của hình trụ.
Cách giải:
Kẻ đường sinh
Gọi H là trung điểm
Ta có
Ta có
Mà
Khi đó thể tích khối trụ là
Chọn D.
Câu 34(VD) – Khoảng cách( lớp 11).
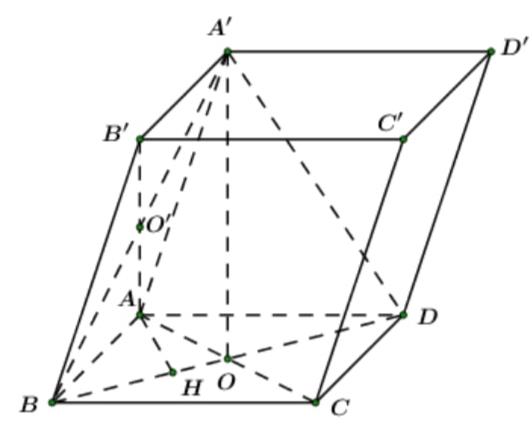
Phương pháp:
Áp dụng các công thức tính khoảng cách.
Cách giải:
Gọi O’ là giao điểm của A’B và AB’
Ta có
Kẻ
Ta có
Áp dụng hệ thực lượng trong tam giác ABD vuông tại A có đường cao AH ta có:
Chọn D.
Câu 35(NB) – Đạo hàm của hàm số.
Phương pháp:
Áp dụng tính chất của hàm số.
Cách giải:
Câu C sai vì vẫn có thể là cực trị của hàm số.
Chọn C.
Câu 36(VD) – Nhị thức Niuton.
Phương pháp:
Áp dụng công thức khai triển nhị thức Niuton.
Cách giải:
Ta có
Khi đó
Số hạng chứa là
Hệ số của số hạng chứa là
Chọn A.
Câu 37)VD) – Nguyên hàm, tích phân.
Phương pháp:
Áp dụng các tính chất của nguyên hàm, tích phân.
Cách giải:
Giả sử
Ta có
Do đó hàm số có dạng
Mà
Nên
Khi đó
Chọn B.
Câu 38(TH) – Góc giữa đường thẳng và mặt phẳng.
Phương pháp:
Áp dụng các tính chất vuông góc và công thức lượng giác.
Cách giải:
Ta có là hình chiếu của S trên mặt phẳng ABCD
Nên
Hình vuông ABCD có cạnh a nên
Tam giác SAC vuông nên
Chọn A.
Câu 39(VD) – Hệ tọa độ trong không gian.
Phương pháp:
Áp dụng công thức tính tọa độ trong không gian.
Cách giải:
Gọi I là điểm bất kì sao cho
Khi đó đạt giá trị nhỏ nhât khi
M là hình chiếu của I trên mặt phẳng
Khi đó
Chọn B.
Câu 40(VD) – Phương trình lượng giác.
Phương pháp:
Áp dụng các tính chất của phương trình lượng giác.
Cách giải:
Ta có
Mà
Dấu bằng xảy ra khi
có 1285 nghiệm
Khi đó tổng các nghiệm của phương trình là
Chọn B.
Câu 41(NB) – Hàm số mũ.
Phương pháp:
Áp dụng tính chất của hàm số mũ.
Cách giải:
Hàm số xác định khi
Chọn B.
Câu 42(TH) – Nguyên hàm.
Phương pháp:
Sử dụng các công thức tính nguyên hàm.
Cách giải:
Ta có
Chọn C.
Câu 43(TH) – Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích hình chóp, hình hộp chữ nhật.
Cách giải:
Tứ diện BDB’C’ có là đường cao tứ diện
Nên
Chọn D.
Câu 44(VD) – Phương trình.
Phương pháp:
Đặt ẩn phụ.
Giải và biện luận phương trình
Cách giải:
Ta có
Xét
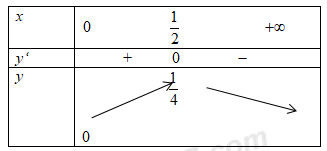
Xét
Để phương trình có 3 nghiệm thì
Chọn B.
Câu 45(VD) – Nguyên hàm, tích phân.
Phương pháp:
Sử dụng các công thức tính đạo hàm, nguyên hàm, tích phân.
Cách giải:
Ta có có nguyên hàm là
Nên
Chọn C.
Câu 46(VD) – Tích phân.
Phương pháp:
Áp dụng các tính chất cộng trừ tích phân.
Cách giải:
Ta có
Mà
Nên
Chọn A.
Câu 47(VD) – Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích theo tích phân.
Cách giải:
Do đường kính đáy bình bằng 2dm nên bán kính đáy bình là 1dm
Tương tự, bán kính miệng bình là 2dm.
Ta có
Vậy
Chọn D.
Câu 48(TH) – Phương trình mặt cầu.
Phương pháp:
Tìm tâm của mặt cầu, bán kính mặt cầu.
Viết phương trình mặt cầu.
Cách giải:
Ta có có trung điểm
Nên bán kính mặt cầu đường kính AB là
Khi đó phương trình mặt cầu là
Chọn A.
Câu 49(TH) – Hàm logarit.
Phương pháp:
Áp dụng các tính chất của hàm logarit.
Cách giải:
Ta có
Chọn A.
Câu 50(NB) – Thể tích khối đa diện.
Phương pháp:
Áp dụng công thức tính thể tích khối trụ.
Cách giải:
Khối trụ có bán kính đáy bằng 6 và chiều cao bằng 3
Chọn B.
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 8
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 8)
Câu 1: Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?
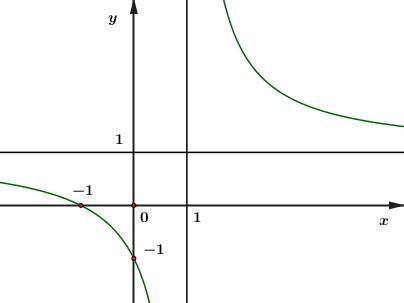
A.
B.
C.
D.
Câu 2: Số tiếp tuyến của đồ thị hàm số song song với trục hoành là :
A. một B. ba C. hai D. không
Câu 3: Cho hàm số có bảng biến thiên như sau:
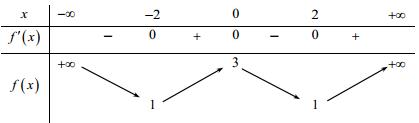
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. B.
C. D.
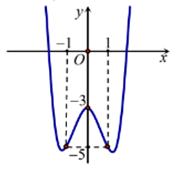
Câu 4: Cho hàm số có đồ thị như hình vẽ
Hàm số đồng biến trên khoảng:
A.
B.
C.
D.
Câu 5: Tổng số mặt, số cạnh và số đỉnh của một hình lập phương là:
A. 26 B. 24 C. 30 D. 22
Câu 6: Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là một hình thoi cạnh a, ; Tính khoảng cách giữa hai đường thẳng A’C và BB’?
A. B.
C. D.
Câu 7: Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A. và
B. và
C. và
D. và
Câu 8: Cho hàm số có đạo hàm Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên các khoảng
B. Hàm số nghịch biến trên khoảng
C. Hàm số nghịc biến trên các khoảng
D. Hàm số đồng biến trên khoảng
Câu 9: Có bao nhiêu điểm thuộc đồ thị hàm số thỏa mãn tiếp tuyến với đồ thị tại điểm đó có hệ số góc bằng 2018?
A. 1 B. 0 C. Vô số D. 2
Câu 10: Số giao điểm của đồ thị hàm số và đường thẳng là:
A. B. C. D.
Câu 11: Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết và SC hợp với (SAB) một góc 300 và (SAC) hợp với (ABC) một góc 600. Thể tích khối chóp là:
A.
B.
C.
D.
Câu 12: Số đường tiệm cận của đồ thị hàm số là:
A. 2 B. 0 C. 1 D. 3
Câu 13: Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, ABB'A', ADD'A' lần lượt bằng , , . Tính thể tích khối A.A'B'D'.
A. B.
C. D.
Câu 14: Cho hàm số có bảng biến thiên như hình vẽ
Đồ thị hàm số có 5 điểm cực trị khi và chỉ khi
A. .
B. .
C. .
D. .
Câu 15: Một đường thẳng cắt đồ thị hàm số tại 4 điểm phân biệt có hoành độ và n. Tính
A. B.
C. D.
Câu 16: Đồ thị sau đây là của hàm số Với giá trị nào của m thì phương trình có đúng 3 nghiệm phân biệt.
A. B.
C. D.
Câu 17: Cho khối chóp S.ABC có , , , , Tính thể tích khối chóp S.ABC.
A. B. C. D.
Câu 18: Đồ thị hàm số có bao nhiêu đường tiệm cận
A. . B. . C. . D. .
Câu 19: Xét các khẳng định sau
i) Nếu hàm số có đạo hàm cấp hai trên và đạt cực tiểu tại thì
ii) Nếu hàm số có đạo hàm cấp hai trên và đạt cực đại tại thì
iii) Nếu hàm số có đạo hàm cấp hai trên và thì hàm số không đạt cực trị tại
Số khẳng định đúng trong các khẳng định trên là
A. B. C. D.
Câu 20: Gọi I là tâm đối xứng của đồ thị hàm số . Tìm tọa độ điểm .
A. B. . C. D. .
Câu 21: Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BC' và B'D' là:
A. . B. . C. . D. .
Câu 22: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn. Tính .
A. B. C. D.
Câu 23: Khối đa diện đều loại có bao nhiêu mặt?
A. 12 mặt B. 6 mặt C. 10 mặt D. 8 mặt
Câu 24: Cho hàm số liên tục trên và có đạo hàm . Khẳng định nào dưới đây đúng ?
A. Hàm số đồng biến trên các khoảng và
B. Hàm số có ba điểm cực trị
C. Hàm số đồng biến trên khoảng
D. Hàm số đạt cực đại tại và đạt cực tiểu tại và
Câu 25: Cho hình chóp S.ABCD có đáy là hình thoi cạnh , , cạnh bên và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ đến mặt phẳng .
A. B.
C. D.
Câu 26: Cho hàm số . Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số nghịch biến trên các khoảng và .
B. Hàm số đồng biến trên các khoảng và .
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên .
Câu 27: Tìm giá trị nhỏ nhất của hàm số trên
A.
B.
C.
D.
Câu 28: Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy, và Góc giữa đường thẳng SB và mặt phẳng bằng
A. B. C. D.
Câu 29: Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào sau đây sai?
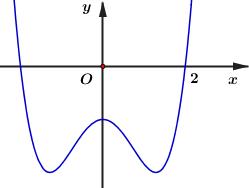
A. B.
C. D.
Câu 30: Cho hàm số có đạo hàm trên . Phát biểu nào sau đây là sai?
A. thì hàm số gọi là nghịch biến trên
B. Hàm số gọi là nghịch biến trên khi và chỉ khi và tại hữu hạn giá trị .
C. Hàm số gọi là nghịch biến trên khi và chỉ khi
D. Hàm số gọi là nghịch biến trên khi và chỉ khi .
Câu 31: Gọi , là hai điểm cực trị của đồ thị hàm số . Giá trị bằng
A. 0. B. 3. C. D.
Câu 32: Đồ thị hình bên là của hàm số nào? 
A. .
B. .
C. .
D. .
Câu 33: Cho hàm số có đạo hàm . Tìm số điểm cực trị của .
A. 0 B. 1 C. 2 D. 3
Câu 34: Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ bên. Gọi và lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn . Tính .
A. 5 B. 8 C. 7 D. 1
Câu 35: Khẳng định nào dưới đây về hàm số là đúng?
A. Hàm số đạt cực tiểu tại
B. hàm số có cực đại, không có cực tiểu
C. Hàm số có một cực đại và 2 cực tiểu
D. Hàm số không có cực trị
Câu 36: Cho hình chóp S.ABC có lần lượt là trung điểm của . Biết thể tích khối chóp S.ABC bằng 24. Tính thể tích của khối chóp S.A'B'C.
A. . B. .
C. . D. .
Câu 37: Cho biết bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó.
A. .
B. .
C. .
D. .
Câu 38: Cho hình chóp đều S.ABC có độ dài cạnh đáy là 2a, mặt bên tạo với mặt đáy một góc . Tính thế tích của khối chóp S.ABC?
A. B.
C. D.
Câu 39: Tìm để đường thẳng cắt đồ thị hàm số tại hai điểm sao cho độ dài MN nhỏ nhất:
A. 3 B. -1 C. 2 D. 1
Câu 40: Cho khối chóp tam giác có thể tích bằng 6. Gọi lần lượt là trung điểm các cạnh . Thể tích của khối chóp S.MNP là?
A. B.
C. D.
Câu 41: Gọi là hai điểm cực trị của đồ thị hàm số . Phương trình đường thẳng đi qua hai điểm là:
A. B.
C. D.
Câu 42: Cho hàm số có đồ thị là . Viết phương trình tiếp tuyến với đồ thị biết tiếp tuyến có hệ số góc
A.
B.
C.
D.
Câu 43: Đáy của hình chóp S.ABCD là một hình vuông cạnh . Cạnh bên SA vuông góc với mặt phẳng đáy và có độ dài là . Thể tích khối tứ diện S.BCD bằng:
A. B. C. D.
Câu 44: Khối lăng trụ ABCA'B'C' có đáy là tam giác đều, a là độ dài cạnh đáy. Góc giữa cạnh bên và đáy là Hình chiếu vuông góc của A’ trên mặt phẳng trùng với trung điểm của BC. Thể tích của khối lăng trụ đã cho là
A. B.
C. D.
Câu 45: Trung điểm của tất cả các cạnh của hình tứ diện đều là các đỉnh của khối đa diện nào?
A. Hình hộp chữ nhật. B. Hình bát diện đều.
C. Hình lập phương. D. Hình tứ diện đều.
Câu 46: Cho hàm số liên tục trên và có đồ thị như hình bên. Số nghiệm dương phân biệt của phương trình là
A. 1 B. 4 C. 2 D. 3
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy (tham khảo hình vẽ bên). Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
A. SDA B. SCA C. SCB D. ASD
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, , SC tạo với đáy một góc . Tính khoảng cách từ A đến mặt phẳng (SBD).
A. B.
C. D.
Câu 49: Biết rằng phương trình có nghiệm khi với . Khi đó giá trị của là
A. B. . C. . D. .
Câu 50: Tập hợp tất cả các giá trị thực của tham số để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt là:
A.
B.
C.
D.
Lời giải chi tiết
|
1. B |
2. C |
3. C |
4. A |
5. A |
|
6. C |
7. A |
8. D |
9. B |
10. C |
|
11. A |
12. A |
13. B |
14. C |
15. D |
|
16. B |
17. B |
18. A |
19. A |
20. A |
|
21. C |
22. C |
23. A |
24. C |
25. A |
|
26. D |
27. A |
28. B |
29. C |
30. D |
|
31. D |
32. B |
33. C |
34. A |
35. B |
|
36. C |
37. D |
38. A |
39. A |
40. B |
|
41. C |
42. D |
43. A |
44. D |
45. B |
|
46. C |
47. A |
48. A |
49. B |
50. A |
Câu 1:
Phương pháp:
Dựa vào đồ thị hàm số, nhận xét các đường TCĐ, TCN và các điểm mà đồ thị hàm số đi qua để chọn đáp án đúng.
Cách giải:
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có TCĐ là loại đáp án A.
Đồ thị hàm số đi qua điểm và chọn đáp án B.
Chọn B.
Câu 2:
Phương pháp:
Tìm số nghiệm của phương trình .
Cách giải:
Phương trình trục hoành: .
Ta có Hệ số góc của tiếp tuyến tại điểm có hoành độ là .
Tiếp tuyến // Ox .
Khi ta tìm được hai tiếp tuyến trùng nhau là
Vậy có hai tiếp tuyến song song với trục hoành.
Chọn C.
Câu 3:
Phương pháp:
Dựa vào BBT để nhận xét tính đơn điệu của hàm số.
+) Hàm số đồng biến trên
+) Hàm số nghịch biến trên
Cách giải:
Dựa vào BBT ta thấy hàm số nghịch biến trên các khoảng và
Chọn C.
Câu 4:
Cách giải:
Dựa vào hình vẽ ta nhận thấy hàm số đồng biến trên .
Chọn A.
Câu 5:
Phương pháp:
Hình lập phương là hình có mặt đều là các hình vuông.
Cách giải:
Hình lập phương có mặt, đỉnh và 12 cạnh nên tổng số cạnh, mặt đỉnh là: .
Chọn A.
Câu 6:
Phương pháp:
Xác định mặt phẳng chứa đường này và song song với đường kia, đưa về bài toán tính khoảng cách từ 1 điểm đến 1 mặt phẳng.
Cách giải:
Ta có
Gọi ta có :
Tam giác A’B’D’ là tam giác đều cạnh a
Chọn C.
Câu 7:
Phương pháp:
+) Đường thẳng được gọi là TCĐ của đồ thị hàm số .
+) Đường thẳng được gọi là TCN của đồ thị hàm số .
Cách giải:
TXĐ:
Ta có: là TCN của đồ thị hàm số.
là TCĐ của đồ thị hàm số.
Chọn A.
Câu 8:
Phương pháp:
- Lập bảng biến thiên.
- Lưu ý: nghiệm bậc chẵn thì không đổi dấu, nghiệm bậc lẻ thì đổi dấu.
Cách giải:
Ta có
Lập bảng xét dấu ta có:
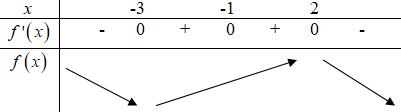
Dựa vào bảng biến thiên ta thấy:
Hàm số đồng biến trên và nghịch biến trên
Chọn D.
Câu 9:
Phương pháp:
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là .
Cách giải:
Đk: .
Ta có: .
Hoành độ của các điểm thuộc đồ thị hàm số mà tiếp tuyến tại đó có hệ số góc bằng 2018 là nghiệm của phương trình
(vô nghiệm) nên không có điểm nào thỏa mãn.
Chọn B.
Câu 10:
Phương pháp:
Giải phương trình hoành độ giao điểm, số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số.
Cách giải:
Xét phương trình hoành độ giao điểm .
Vậy đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt
Chọn C.
Câu 11:
Cách giải:
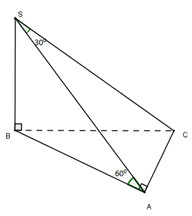
Ta có:
SA là hình chiếu vuông góc của SC trên (SAB) ⇒
vuông tại B
Xét tam giác vuông SAC ta có:
⇒
⇒
Chọn A.
Câu 12:
Phương pháp:
Cho hàm số .
+) Nếu là TCN của đồ thị hàm số.
+) Nếu là TCĐ của đồ thị hàm số.
Cách giải:
TXĐ: . Ta có:
Do đó đồ thị hàm số có TCN .
Ta có
, do đó đồ thị hàm số có TCĐ .
Xét phương trình
Vậy hàm số có 1 TCN và 1 TCĐ .
Chọn A.
Câu 13:
Phương pháp:
- Tính thể tích khối hộp ABCD.A'B'C'D'.
- So sánh thể tích chóp A.A'B'D' với thể tích khối hộp ABCD.A'B'C'D'.
Cách giải:
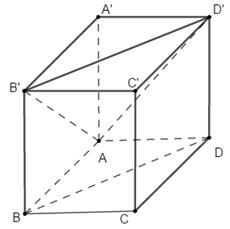
Đặt
Ta có diện tích hình chữ nhật ABCD, ABB'A', ADD'A' lần lượt là , , .
Suy ra .
Ta có:
.
Chọn B.
Câu 14:
Phương pháp:
Đồ thị hàm số có 5 điểm cực trị khi và chỉ khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
Cách giải:
Đồ thị hàm số có 5 điểm cực trị khi và chỉ khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt .
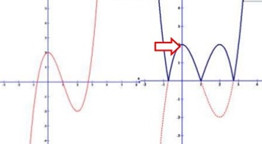
Chọn C.
Câu 15:
Phương pháp:
Hoành độ giao điểm của đường thẳng d và đồ thị hàm số (C) là nghiệm của phương trình hoành độ giao điểm của hai đồ thị hàm số.
Dựa vào các hoành độ đã biết, tìm được phương trình đường thẳng d từ đó ta xác định được m, n và tính giá trị của biểu thức.
Cách giải:
Gọi phương trình đường thẳng bài cho là:
Đường thẳng cắt đồ thị hàm số tại hai điểm có hoành độ là tọa độ hai điểm đó là:
Khi đó ta có phương trình hoành độ giao điểm của hai đồ thị hàm số là:
Khi đó là hai nghiệm của phương trình
Áp dụng hệ thức Vi-ét ta có:
Chọn D.
Câu 16:
Phương pháp:
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số và đường thẳng
Dựa vào đồ thị hàm số để xác định m thỏa mãn bài toán.
Cách giải:
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số và đường thẳng
Dựa vào đồ thị hàm số ta thấy đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt
Chọn B.
Câu 17:
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy và chiều cao là:
Cách giải:
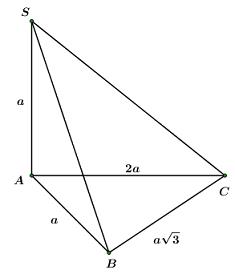
Ta có:
vuông tại (định lý Pitago đảo)
Chọn B.
Câu 18:
Phương pháp:
- Tìm TXĐ của hàm số.
- Dựa vào định nghĩa để xác định các đường tiệm cận của đồ thị hàm số .
+ Đường thẳng là đường tiệm cận ngang của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: , .
+ Đường thẳng là đường tiệm cận đứng của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: , , , .
Cách giải:
TXĐ: .
Ta có
là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả 4 đường tiệm cận.
Chọn A.
Câu 19:
Phương pháp:
Dựa vào điều kiện cần để hàm số có cực trị.
Cách giải:
Giả sử hàm số có đạo hàm trên và chứa thỏa mãn và có đạo hàm cấp hai khác tại điểm thì:
+) Hàm số đạt cực đại tại khi
+) Hàm số đạt cực tiểu tại khi
khẳng định i) và ii) sai.
Khi ta không kết luận về cực trị của hàm số.
khẳng định iii) sai.
Chọn A.
Câu 20:
Phương pháp:
Tâm đối xứng của đồ thị hàm số bậc nhất trên bậc nhất là giao điểm của hai đường tiệm cận của đồ thị hàm số đó.
Cách giải:
Đồ thị hàm số có TCĐ: , TCN:
Tọa độ tâm I là tâm đối xứng của đồ thị hàm số trên là: .
Chọn A.
Câu 21:
Phương pháp:
Sử dụng định lí:
Cách giải:
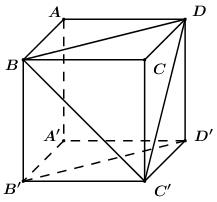
Do nên .
Giả sử cạnh của hình lập phương bằng 1. Áp dụng định lí Pytago trong các tam giác vuông ta có: .
Suy ra tam giác BC'D đều .
Vậy .
Chọn C.
Câu 22:
Phương pháp:
Để tìm GTNN, GTLN của hàm số trên đoạn , ta làm như sau:
- Tìm các điểm thuộc khoảng mà tại đó hàm số có đạo hàm bằng 0 hoặc không có đạo hàm.
- Tính
- So sánh các giá trị vừa tìm được. Số lớn nhất trong các giá trị đó chính là GTLN của trên ; số nhỏ nhất trong các giá trị đó chính là GTNN của trên .
Cách giải:
;
Hàm số liên tục trên , có
.
Chọn C.
Câu 23:
Phương pháp:
Sử dụng công thức trong đó là loại khối đa diện đều, D, C, M lần lượt là số đỉnh, số cạnh, số mặt của khối đa diện.
Cách giải:
Khối đa diện đều loại
chia hết cho 6
Khi thì khối đa diện đều là khối lập phương thuộc loại (ktm).
Vậy .
Chọn A.
Câu 24:
Phương pháp:
Giải phương trình rồi lập BBT.
Lưu ý rằng: Qua nghiệm bội chẵn thì dấu không đổi.
Cách giải:
Ta có :
BBT :
Từ BBT ta thấy hàm số đồng biến trên khoảng nên C đúng.
Hàm số có 2 điểm cực trị.
Chọn C.
Câu 25:
Phương pháp:
- Chứng minh .
- Xác định khoảng cách từ đến .
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Cách giải:
Ta có .
Trong kẻ .
Vì nên điểm nằm ngoài đoạn thẳng CD.
Trong dựng ta có:
.
.
Xét tam giác vuông AHD có , .
Vì nên , suy ra tam giác SAH vuông tại , áp dụng hệ thức lượng trong tam giác vuông ta có: .
Vậy .
Chọn A.
Câu 26:
Phương pháp:
Hàm số phân thức bậc nhất trên bậc nhất đơn điệu trên từng khoảng xác định của chúng.
Cách giải:
TXĐ: .
Ta có: .
Vậy hàm số đồng biến trên các khoảng và . Do đó hàm số đồng biến trên .
Chọn D.
Câu 27:
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số trên :
Bước 1: Tính y’, giải phương trình , suy ra các nghiệm .
Bước 2: Tính các giá trị
Bước 3: So sánh và kết luận:
Cách giải:
TXĐ: .
Ta có:
Chọn A.
Câu 28:
Phương pháp:
Áp dụng phương pháp xác định góc giữa đường thẳng và mặt phẳng
Cách giải:
Kẻ
Suy ra
Tam giác ABH vuông tại H, có
Tam giác SAB vuông tại A, có
Do đó vuông cân tại
Chọn B.
Câu 29:
Phương pháp:
Dựa vào số điểm cực trị và các điểm mà đồ thị hàm số đi qua để chọn đáp án đúng.
Cho hàm số ta có:
+) Hàm số có một cực trị
+) Hàm số có ba cực trị
+) Hàm số có đúng một cực trị và cực trị là cực tiểu
+) Hàm số có đúng một cực trị và cực trị là cực đại
+) Hàm số có hai cực tiểu và một cực đại
+) Hàm số có một cực tiểu và hai cực đại
Cách giải:
Ta thấy đồ thị hàm số cắt trục tung tại điểm có tung độ âm Đáp án D đúng.
Dựa vào đồ thị hàm số ta thấy hàm số đã cho có 3 điểm cực trị, trong đó có 2 điểm cực tiểu và 1 điểm cực đại
Đáp án C sai.
Chọn C.
Câu 30:
Phương pháp:
Sử dụng lý thuyết về hàm số nghịch biến
Cách giải:
Cho hàm số có đạo hàm trên . Khi đó
Hàm số gọi là nghịch biến trên khi và chỉ khi và tại hữu hạn giá trị nên D sai.
Các đáp án A, B, C đều đúng.
Chọn D.
Câu 31:
Phương pháp:
Giải phương trình , tìm tọa độ 2 điểm cực trị. Từ đó tính tổng
Cách giải:
Ta có: .
Vậy tọa độ hai điểm cực trị là .
Chọn D.
Câu 32:
Phương pháp:
Nhận biết đồ thị hàm số bậc 4 trùng phương.
Cách giải:
Hàm số cần tìm có dạng
Quan sát đồ thị hàm số, ta thấy: khi Hệ số Loại phương án A
Đồ thị hàm số cắt Oy tại điểm có tung độ bằng 2 Loại phương án D
Hàm số đạt cực tiểu tại hai điểm chọn phương án B .
Chọn B.
Câu 33:
Phương pháp:
Điểm cực trị của hàm số là điểm mà tại đó y' đổi dấu.
Cách giải:
Trong đó, đổi dấu tại 2 điểm
Hàm số có 2 điểm cực trị.
Chọn C.
Câu 34:
Phương pháp:
GTLN, GTNN của hàm số trên lần lượt là giá trị của điểm cao nhất và điểm thấp nhất của đồ thị hàm số trên .
Cách giải:
Dựa vào đồ thị hàm số ta dễ dàng suy ra được .
Vậy .
Chọn A.
Câu 35:
Phương pháp:
Điểm được gọi là điểm cực đại của hàm số
Điểm được gọi là điểm cực tiểu của hàm số
Cách giải:
Hàm số đạt cực đại tại và không có cực tiểu.
Chọn B.
Câu 36:
Phương pháp:
Sử dụng công thức tính tỉ lệ thể tích: Cho các điểm ta có:
Cách giải:
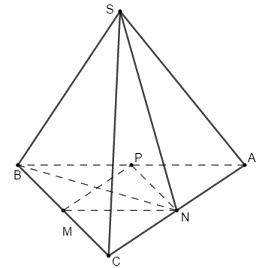
Ta có: lần lượt là trung điểm của
Chọn C.
Câu 37:
Phương pháp:
Dựa vào BBT, nhận xét tính đơn điệu và tập xác định của hàm số và chọn đáp án đúng.
Cách giải:
Dựa vào BBT ta thấy hàm số có TXĐ: hàm số nghịch biến trên từng khoảng xác định và có TCN là
Ta thấy các hàm số ở cả 4 đáp án đều có TXĐ:
Tuy nhiên chỉ có đáp án A và đáp án D là đồ thị hàm số có TCN là đường
+) Xét đáp án A: có hàm số đồng biến trên từng khoảng xác định loại đáp án A.
Chọn D.
Câu 38:
Phương pháp:
- Tìm góc tạo bởi mặt bên và đáy.
- Tính chiều cao của khối chóp
- Thể tích của khối chóp được tính bởi công thức: .
Cách giải:
Gọi là trọng tâm tam giác ABC, là trung điểm BC.
S.ABC là hình chóp đều nên chân đường cao hạ từ xuống mp đáy là trọng tâm của đáy
Suy ra
Tam giác ABC là tam giác đều nên
Ta có: .
Góc giữa mặt bên và mặt đáy bằng nên .
Lại có:.
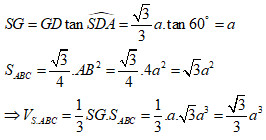
Chọn A.
Câu 39:
Phương pháp:
+) Tìm điều kiện của để hai đồ thị hàm số cắt nhau tại hai điểm phân biệt.
+) Gọi là hai giao điểm của 2 đồ thị hàm số.
+) Khi đó :
+) Sử dụng định lý Vi-et để tìm giá trị của để độ dài MN đạt giá trị nhỏ nhất.
Cách giải:
Phương trình hoành độ giao điểm của 2 đồ thị hàm số là:
Ta có:
luôn có hai nghiệm phân biệt với mọi .
Áp dụng định kí Vi-ét ta có:
Gọi là hai giao điểm của 2 đồ thị hàm số.
Khi đó ta có:
Dấu “=” xảy ra
Chọn A.
Câu 40:
Phương pháp:
Dựa vào tỉ số giữa 2 mặt đáy.
Cách giải:
Ta có M,N,P lần lượt là trung điểm các cạnh BC, CA, AB.
Nên
Chọn B.
Câu 41:
Phương pháp:
Đường thẳng đi qua 2 điểm cực trị của hàm số là số dư khi chia y cho y’.
Cách giải:
Hàm số có đạo hàm
Chia y cho y’ ta có:
Khi đó đường thẳng hay là đường thẳng đi qua 2 điểm cực trị của hàm số.
Chọn C.
Câu 42:
Phương pháp:
+) Cho hàm số có đạo hàm . Khi đó phương trình tiếp tuyến của đồ thị hàm số tại có phương trình: .
+) Cho hệ số góc của tiếp tuyến tại là k .
Cách giải:
Gọi là một điểm thuộc đồ thị .
Ta có .
Tiếp tuyến của đồ thị hàm số tại M có hệ số góc nên ta có:
.
Vậy phương trình tiếp tuyến của đồ thị hàm số tại là: .
Chọn D.
Câu 43:
Cách giải:
Ta có:
Chọn A.
Câu 44:
Phương pháp:
+ Xác định góc giữa cạnh bên và đáy.
+ Tính độ dài đường cao lăng trụ.
+ Áp dụng công thức tính thể tích lăng trụ .
Cách giải:
Gọi là trung điểm của .
.
Tam giác ABC đều cạnh .
Xét tam giác vuông A'AH có: .
Tam giác ABC đều cạnh .
Vậy
Chọn D.
Câu 45:
Phương pháp:
Vẽ hình và quan sát, tính số cạnh và các tính chất của các hình để loại trừ đáp án.
Cách giải:
Giả sử ABCD là tứ diện đều. Gọi lần lượt là trung điểm của Khi đó các trung điểm các cạnh của tứ diện đều tạo thành hình SMNPQT. Do đó SMNPQT không thể là tứ diện đều được. Ta loại đáp án D.
Do là trung điểm của nên
Tương tự ta có Do là tam giác đều nên Kéo theo
Chứng minh tương tự ta nhận được các cạnh của SMNPQT có độ dài như nhau.
Mặt khác từ suy ra là tam giác đều, do đó Do đó SMNPQT không thể là hình hộp chữ nhật hay hình lập phương được. Như vậy đáp án đều bị loại.
Chọn B.
Câu 46:
Phương pháp:
Số nghiệm dương phân biệt của phương trình bằng số giao điểm có hoành độ dương của đồ thị hàm số và đường thẳng .
Cách giải:
Số nghiệm dương phân biệt của phương trình bằng số giao điểm có hoành độ dương của đồ thị hàm số và đường thẳng và bằng 2.
Chọn C.
Câu 47:
Phương pháp:
Xác định góc giữa hai mặt phẳng :
- Tìm giao tuyến của .
- Xác định 1 mặt phẳng .
- Tìm các giao tuyến
- Góc giữa hai mặt phẳng : .
Cách giải:
Ta có:
Mà (ABCD là hình vuông), (vì
Chọn A.
Câu 48:
Phương pháp:
+) Xác định góc giữa SC và (ABCD) là góc SCA.
+) Trong mp(SAC) kẻ chứng minh
Cách giải:
AC là hình chiếu của SC trên (ABCD) vuông cân tại A
Gọi . trong mặt phẳng (SAC) kẻ
Ta có
Ta có
Chọn A.
Câu 49:
Phương pháp:
- Sử dụng phương pháp hàm số.
Cách giải:
Xét hàm số trên , ta có:
Nếu thì vô nghiệm.
Nếu thì vô nghiệm.
Thay vào (1), ta thấy là nghiệm và đồng thời là nghiệm duy nhất của (1).
Ta có bảng biến thiên như sau:
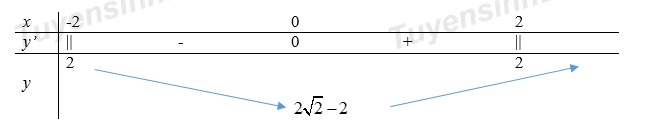
Để phương trình có nghiệm thì .
Chọn B.
Câu 50:
Phương pháp:
Để đường thẳng cắt đồ thị hàm số tại điểm phân biệt thì phương trình cần có nghiệm phân biệt khác
Áp dụng bài toán ta cần tìm điều kiện để có hai nghiệm phân biệt. Đưa phương trình về dạng bậc hai và sử dụng kết quả cho phương trình bậc 2 đã học để giải bài toán.
Cách giải:
Để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt thì phương trình có hai nghiệm phân biệt. Khi đó ta có
Phương trình có hai nghiệm phân biệt khi và chỉ khi
Lưu ý rằng nên khi đó phương trình (1) nếu có nghiệm thì nghiệm này sẽ khác 2. Vậy tập hợp tất cả các giá trị của để đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt là
Chọn A.
Chú ý khi giải: Sai lầm.Vì phương trình nếu có nghiệm thì nghiệm sẽ khác nên trong trường hợp đề thi trắc nghiệm học sinh có thể bỏ qua việc kiểm tra xem có là nghiệm của hay không. Tuy nhiên việc bỏ qua kiểm tra có là nghiệm hay không trong trường hợp tổng quát là một thiếu sót, có thể dẫn tới việc tìm thừa giá trị của .
Đề thi Toán lớp 12 Giữa kì 2 (20 đề) - Đề 9
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Môn: Toán 12
Thời gian làm bài: 90 phút
(Đề 9)
Câu 1: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
A. 3 B. 1 C. 2 D. 4
Câu 2: Cho hàm số y=x2+xx−2 có đồ thị (C). Phương trình tiếp tuyến tại điểm A(1;−2) của (C) là
A. y=−3x+5. B. y=−5x+7
C. y=−5x+3 D. y=−4x+6
Câu 3: Gọi (P) là đồ thị hàm số y=2x3−x+3. Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của (P)?
A. y=−x−3 B. y=11x+4
C. y=−x+3 D. y=4x−1
Câu 4: Khối đa diện đều loại {4;3} có bao nhiêu mặt?
A. 6. B. 20 C. 12 D. 8
Câu 5: Cho lăng trụ ABC.A′B′C′ có các mặt bên là hình vuông cạnh a√2. Tính theo a thể tích V của khối lăng trụ ABC,A’B’C’.
A. V=√6a32 B. V=√3a312
C. V=√3a34 D. V=√6a36
Câu 6: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA=√2a và SA vuông góc với (ABCD). Góc giữa SC và ABCD bằng
A. 450 B. 300 C. 600 D. 900
Câu 7: Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Tính khoảng cách giữa hai đường thẳng AB′ và CD′.
A. √2a2 B. a C. √2a D. 2a
Câu 8: Giá trị cực đại của hàm số y=x3−12x+20 là:
A. yCD=4 B. yCD=36
C. yCD=−4 D. yCD=−2
Câu 9: Tập xác định của hàm số y=1√sinx+1 là
A. R∖{π2+k2π,k∈Z}
B. R∖{−π2+k2π,k∈Z}
C. R∖{−π2+kπ,k∈Z}
D. R
Câu 10: Nghiệm âm lớn nhất của phương trình √3sin2x=3cotx+√3 là
A. −π6. B. −5π6.
C. −π2. D. −2π3.
Câu 11: Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17... Tìm công thức số hạng tổng quát un của cấp số cộng?
A. un=5n−1. B. un=5n+1.
C. un=4n−1 D. un=4n+1
Câu 12: Tìm giá trị nhỏ nhất của hàm số y=x2−1 trên đoạn [−3;2]?
A. min[−3;2]y=3 B. min[−3;2]y=−3
C. min[−3;2]y=−1 D. min[−3;2]y=8
Câu 13: Cho hàm số y=√x2−1. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (0;+∞)
B. Hàm số nghịch biến trên khoảng (−∞;0)
C. Hàm số đồng biến trên khoảng (1;+∞)
D. Hàm số đồng biến trên khoảng (un)
Câu 14: Khai triển (x−3)100 ta được đa thức (x−3)100=a0+a1x+a2x2+...+a100x100, a1,a2,...,a100 là các hệ số thực. Tính a0−a1+a2−...−a99+a100?
A. −2100 B. 4100
C. −4100 D. 2100
Câu 15: Nghiệm của phương trình lượng giác cos2x−cosx=0 thỏa mãn điều kiện 0<x<π là:
A. x=0 B. x=3π4
C. x=π2 D. x=−π2
Câu 16: Tất cả các nghiệm của phương trình tanx=cotx là:
A. x=π4+kπ4,k∈Z
B. x=π4+k2π,k∈Z
C. x=π4+kπ,k∈Z
D. x=π4+kπ2,k∈Z
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA=a√2 và vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABC?
A. V=√26a3 B. V=2√23a3
C. V=√2a3 D. V=√23a3
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB=a,SA=a√3 và vuông góc với (ABCD). Tính góc giữa hai đường thẳng SB và CD.
A. 600 B. 300 C. 450 D. 900
Câu 19: Cho hàm số y=3x−1x−3 có đồ thị (C). Mệnh đề nào sau đây sai?
A. Đồ thị (C) có tiệm cận ngang và tiệm cận đứng.
B. Đồ thị (C) không có tiệm cận đứng.
C. Đồ thị (C) có tiệm cận ngang.
D. Đồ thị (C) có tiệm cận.
Câu 20: Trong năm học 2018-2019 trường THPT chuyên đại học Vinh có 13 học sinh khối 10, 12 học sinh khối 11, 12 học sinh khối 12. Nhân ngày nhà giáo Việt Nam 20 tháng 11 nhà trường chọn ngẫu nhiên 2 lớp trong trường để tham gia hội văn nghệ của trường Đại học Vinh. Xác suất để chọn được hai lớp không cùng khối là:
A. 76111 B. 87111 C. 78111 D. 67111
Câu 21: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A,BC=2a, SA=a và SA vuông góc với đáy. Tính góc giữa hai mặt phẳng (SBC) và (ABC)?
A. 450 B. 300 C. 600 D. 900
Câu 22: Gọi x1,x2,x3 là các cực trị của hàm số y=−x4+4x2+2019. Tính tổng x1+x2+x3
A. 0 B. 2√2 C. −1 D. 2
Câu 23: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=x3−3x2−9x+1 trên đoạn [0;4]. Tính tổng m+2M.
A. m+2M=17
B. m+2M=−37
C. m+2M=51
D. m+2M=−24
Câu 24: Cho cấp số nhân (un) thỏa mãn {u1−u3+u5=65u1+u7=325. Tính u3?
A. u3=15 B. u3=25
C. u3=10 D. u3=20
Câu 25: Biết số tự nhiên n thỏa mãn C1n+2C2nC1n+...+nCnnCn−1n=45. Tính Cnn+4?
A. 715. B. 1820 C. 1365 D. 1001
Câu 26: Tìm tất cả các giá trị của m để hàm số y=x−1x+m đồng biến trên khoảng (0;+∞)?
A. (−1;+∞) B. [0;+∞)
C. (0;+∞) D. [−1;+∞)
Câu 27: Tìm tất cả các giá trị thực của tham số m sao cho điểm cực tiểu của đồ thị hàm số y=x3+x2+mx−1 nằm bên phải trục tung?
A. m<0 B. 0<m<13
C. m<13 D. Không tồn tại
Câu 28: Trên một cái bảng đã ghi sẵn các số tự nhiên từ 1 đến 2020. Ta thực hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng là:
A. 4040 B. 2041210 C. 4082420 D. 2020
Câu 29: Số nghiệm của phương trình sin5x+√3cos5x=2sin7x trên khoảng (0;π2)là?
A. 4. B. 1. C. 3. D. 2.
Câu 30: Cho hàm số f(x) có đạo hàm trên R và f′(x)>0,∀x∈R. Biết f(1)=2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2)+f(3)=4
B. f(−1)=2
C. f(2)=1
D. f(2018)<f(2019)
Câu 31: Cho tập hợp A={0;1;2;3;4;5;6}. Từ A lập được bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau và nhỏ hơn 4012.
A. 180 B. 240 C. 200 D. 220
Câu 32: Một vật chuyển động theo quy luật s=−12t3+9t2 với t (giây) là khoảng thời gian tứ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 216(m/s) B. 400(m/s)
C. 54(m/s) D. 30(m/s)
Câu 33: Tất cả các giá trị của tham số m để hàm số y=(m−1)x4 đạt cực đại tại x=0 là:
A. m<1 B. m>1
C. không tồn tại m D. m=1
Câu 34: Tung hai con súc sắc 3 lần độc lập với nhau. Tính xác suất để có đúng một lần tổng số chấm xuất hiện ở hai con súc sắc bằng 6. (Kết quả làm tròn đến 3 chữ số phần thập phân)
A. 0,120 B. 0,319 C. 0,718 D. 0,309
Câu 35: Hệ số của x5 trong khai triển (1−2x−3x2)9 là:
A. 792 B. −684 C. 3528 D. 0
Câu 36: Cho một khối đa diện lỗi có 10 đỉnh, 7 mặt. Hỏi khối đa diện có mấy cạnh?
A. 20 B. 18 C. 15 D. 12
Câu 37: Cho hình chóp S.ABC có đáy là ΔABC vuông cân ở B,AC=a√2,SA⊥(ABC), SA=a. Gọi G là trọng tâm của ΔSBC, mp(α) đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi Vlà thể tích của khối đa diện không chứa đỉnh S. Tính V.
A. 5a354. B. 4a39.
C. 2a39. D. 4a327.
Câu 38: Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=2a, AD=a, AA′=a√3. Gọi M là trung điểm cạnh AB. Tính khoảng cách h từ điểm D đến mặt phẳng (B′MC).
A. h=3a√217 B. h=a√21
C. h=a√2114 D. h=2a√217
Câu 39: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), ^SAB=300,SA=2a. Tính thể tích V của khối chóp S.ABCD.
A. V=√3a36. B. V=a3.
C. V=a39. D. V=a33.
Câu 40: Số tiệm cận ngang của đồ thị hàm số y=|x|−2018x+2019 là:
A. 1 B. 3 C. 2 D. 0
Câu 41: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M,N lần lượt là trung điểm các cạnh SA,SB và P là điểm bất kỳ thuộc cạnh CD. Biết thể tích khối chóp S.ABCD là V. Tính thể tích của khối tứ diện AMNP theo V.
A. V8 B. V12 C. V6 D. V4
Câu 42: Đồ thị hàm số f(x)=x3+ax2+bx+c tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x=1 tại điểm có tung độ bằng 3 khi
A. a=b=0,c=2
B. a=c=0,b=2
C. a=2,b=c=0
D. a=2,b=1,c=0
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA=2a. Khi đó góc giữa đường thẳng SB và mặt phẳng (SAC) bằng:
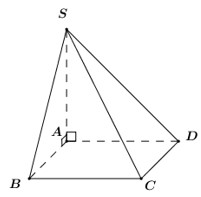
A. 900 B. 450 C. 600 D. 300
Câu 44: Trong mặt phẳng Oxy, có bao nhiêu điểm mà từ đó kẻ được hai tiếp tuyến đến đồ thị hàm số y=x33−x22+x+1 sao cho hai tiếp tuyến này vuông góc với nhau?
A. 0 B. 1 C. 2 D. Vô số
Câu 45: Cho lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác cân tại C ,∠BAC=30∘, AB=a√3, AA′=a. Gọi M là trung điểm của BB′. Tính theo a thể tích V của khối tứ diện MACC′.
A. V=a3√312 B. V=a3√34
C. V=a3√33 D. V=a3√318
Câu 46: Cho hàm số f(x) có f(2)=f(−2)=0 và có bảng xét dấu của đạo hàm như sau:

Hàm số y=(f(3−x))2 nghịch biến trên khoảng nào dưới đây?
A. (2;5) B. (1;+∞)
C. (−2;−1) D. (1;2)
Câu 47: Cho hàm số y=f(x) có bảng biến thiên như sau:
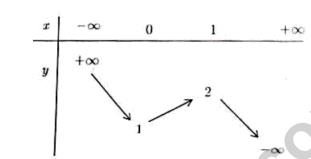
Khi đó số nghiệm của phương trình 2|f(2x−3)|−5=0 là:
A. 3 B. 2 C. 4 D. 1
Câu 48: Tìm số tiệm cận (bao gồm cả tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số y=√4x2+5√2x+1−x−1.
A. 3 B. 1 C. 2 D. 4
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, biết AB=BC=a, AD=2a và SA vuông góc với mặt phẳng đáy, SA=a√2 Xác định số đo của góc φ là góc giữa hai mặt phẳng (SCD) và (SAD).
A. φ=600 B. φ=450
C. φ=300 D. φ=900
Câu 50: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y=mx33+7mx2+14x−m+2 nghịch biến trên [1;+∞).
A. (−∞;−1415) B. (−∞;−1415]
C. [−2;−1415] D. [−1415;+∞)
Lời giải chi tiết
Câu 1:
Phương pháp:
Vẽ hình và đếm.
Cách giải:
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng.
Chọn D.
Câu 2:
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm là:
Cách giải:
TXĐ: .
Ta có
Tiếp tuyến tại có hệ số góc là .
Vậy tiếp tuyến tại của đồ thị hàm số là: .
Chọn C.
Câu 3:
Phương pháp:
Hai đồ thị hàm số và tiếp xúc với nhau khi và chỉ khi hệ phương trình có nghiệm.
Cách giải:
Xét đáp án C: .
Ta có: .
Xét hệ phương trình .
Vậy đường thẳng tiếp xúc với đồ thị hàm số tại điểm có hoành độ bằng 0.
Chọn C.
Câu 4:
Phương pháp:
Vẽ hình và đếm số mặt.
Cách giải:
Khối đa diện đều loại là hình lập phương và có 6 mặt.
Chọn A.
Câu 5:
Phương pháp:
- Tìm chiều cao hình lăng trụ.
- Áp dụng công thức tính thể tích có chiều cao , diện tích đáy là .
Cách giải:
Vì các mặt bên của lăng trụ là hình vuông nên ta có và .
Đồng thời là tam giác đều cạnh .
Vậy .
Chọn A.
Câu 6:
Phương pháp:
- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu vuông góc của nó trên mặt phẳng đó.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Cách giải:
Ta có là hình chiếu vuông góc của lên .
.
Vì là hình vuông cạnh nên vuông cân tại .
Vậy .
Chọn A.
Câu 7:
Phương pháp:
- Tìm đoạn vuông góc chung của hai đường thẳng.
- Khoảng cách giữa hai đường thẳng chéo nhau bằng độ dài đoạn vuông góc chung của chúng.
Cách giải:
Ta có .
Chọn B.
Câu 8:
Phương pháp:
- Hàm số đạt cực đại đại điểm khi và chỉ khi (hàm đa thức bậc ba).
- Thay điểm cực đại của hàm số vào hàm số để tìm giá trị cực đại.
Cách giải:
Ta có: .
Xét hệ là điểm cực đại của hàm số.
Ta có: .
Chọn B.
Câu 9:
Phương pháp:
- Hàm số xác định khi và chỉ khi .
- Sử dụng tính chất: .
Cách giải:
Hàm số xác định khi và chỉ khi .
Ta có: .
Do đó .
Vậy TXĐ của hàm số là .
Chọn B.
Câu 10:
Phương pháp:
- Tìm ĐKXĐ của phương trình.
- Sử dụng công thức .
- Giải phương trình bậc hai đối với một hàm số lượng giác.
- Giải bất phương trình , tìm số nguyên lớn nhất thỏa mãn, từ đó tìm nghiệm âm lớn nhất của phương trình.
Cách giải:
ĐKXĐ: .
Ta có:
+ Xét họ nghiệm .
Cho .
Mà Nghiệm âm lớn nhất là .
+ Xét họ nghiệm .
Cho .
Mà Nghiệm âm lớn nhất là .
Ta có: .
Vậy nghiệm âm lớn nhất của phương trình là .
Chọn C.
Câu 11:
Phương pháp:
- Xác định số hạng đầu và công sai của cấp số cộng.
- Cấp số cộng có số hạng đầu và công sai có SHTQ: .
Cách giải:
Dãy số có số hạng đầu và công sai .
Vậy SHTQ của cấp số cộng trên là .
Chọn D.
Câu 12:
Phương pháp:
- Tính đạo hàm của hàm số, giải phương trình xác định các nghiệm .
- Tính các giá trị: .
- Kết luận: , .
Cách giải:
TXĐ: .
Ta có .
.
Vậy .
Chọn C.
Câu 13(:
Phương pháp:
- Tìm TXĐ của hàm số.
- Tính đạo hàm, lập BXD và kết luận các khoảng đồng biến, nghịch biến của hàm số.
Cách giải:
TXĐ: .
Ta có .
Bảng xét dấu:
![]()
Từ BXD ta thấy hàm số đồng biến trên khoảng là mệnh đề đúng.
Chọn C.
Câu 14:
Phương pháp:
Tìm để tìm đáp án.
Cách giải:
Ta thấy
.
Chọn B.
Câu 15:
Phương pháp:
- Đưa phương trình về dạng phương trình tích.
- Giải phương trình lượng giác cơ bản.
- Tìm các nghiệm thỏa mãn .
Cách giải:
Ta có
.
+ Xét họ nghiệm .
Ta có: .
Mà .
+ Xét họ nghiệm .
Ta có: .
Mà .
Vậy phương trình đã cho có duy nhất 1 nghiệm thỏa mãn là .
Chọn C.
Câu 16:
Phương pháp:
- Tìm ĐKXĐ của phương trình.
- Sử dụng công thức .
- Giải phương trình tìm , sau đó giải phương trình lượng giác cơ bản .
Cách giải:
ĐKXĐ: .
Ta có
Chọn D.
Câu 17:
Phương pháp:
Áp dụng công thức tính thể tích khối chóp có chiều cao , diện tích đáy là .
Cách giải:
Ta có .
Chọn A.
Câu 18:
Phương pháp:
- Sử dụng định lí: .
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Cách giải:
Ta có .
Xét vuông tại có: .
Vậy .
Chọn A.
Câu 19:
Phương pháp:
Đồ thị hàm số có TCN và TCĐ .
Cách giải:
Hàm số có là tiệm cận đứng và là tiệm cận ngang.
Chọn B.
Câu 20:
Phương pháp:
Sử dụng các công thức tính tổ hợp, chỉnh hợp.
Cách giải:
Cả 3 khối có tất cả (học sinh).
Số cách chọn 2 học sinh bất kì là: cách.
Gọi A là biến cố: “Chọn 2 học sinh không cùng khối” : “Chọn 2 học sinh cùng khối”.
Số cách chọn 2 học sinh cùng khối là (cách)
Vậy xác suất của biến cố A là .
Chọn A.
Câu 21:
Phương pháp:
- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tỉ số lượng giác để tính góc.
Cách giải:
Gọi là trung điểm của .
Vì vuông cân tại nên và .
Ta có: .
.
Xét tam giác vuông có: .
Vậy .
Chọn A.
Câu 22:
Phương pháp:
Tìm đạo hàm và tìm cực trị của hàm số.
Cách giải:
Ta có .
Chọn A.
Câu 23:
Phương pháp:
- Tính đạo hàm của hàm số, giải phương trình xác định các nghiệm .
- Tính các giá trị: .
- Kết luận: , .
Cách giải:
Ta có
Bảng biến thiên:
Dựa vào bảng ta thấy giá trị lớn nhất ; giá trị nhỏ nhất .
Vậy .
Chọn D.
Câu 24:
Phương pháp:
- Áp dụng công thức SHTQ của cấp số nhân có số hạng đầu , công bội là .
- Giải hệ phương trình 2 ẩn.
Cách giải:
Gọi công bội của CSN là ta có
.
.
Vậy .
Chọn D.
Câu 25:
Phương pháp:
- Áp dụng công thức tính tổ hợp: .
- Giải phương trình tìm .
Cách giải:
Xét SHTQ:
Khi đó ta có:
Khi đó
Chọn A.
Câu 26:
Phương pháp:
Hàm số đồng biến trên .
Cách giải:
TXĐ: .
Ta có .
Để hàm số đồng biến trên khoảng khi .
Vậy .
Chọn B.
Câu 27:
Phương pháp:
- Tính .
- Tìm điều kiện để phương trình có 2 nghiệm phân biệt.
- Hàm đa thức bậc ba có 2 điểm cực tiểu và thì .
- Giải phương trình tìm .
Cách giải:
TXĐ: .
Ta có: .
Để hàm số có 2 điểm cực trị thì phương trình phải có 2 nghiệm phân biệt
Khi đó ta có .
Vì hàm số có hệ số nên , do đó .
Theo bài ra ta có .
Kết hợp điều kiện ta có .
Chọn A.
Câu 28:
Phương pháp:
Sử dụng công thức tính tổng .
Cách giải:
Thực hiện liên tiếp việc xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng sẽ là tổng của các số tự nhiên từ 1 đến 2020.
Vậy số còn lại trên bảng là .
Chọn B.
Câu 29:
Phương pháp:
Chia cả 2 vế phương trình cho 2.
Cách giải:
Ta có
Mà
Vậy phương trình đã cho có 4 nghiệm thỏa mãn.
Chọn A.
Câu 30:
Phương pháp:
Áp dụng tính chất của hàm đồng biến.
Cách giải:
Vì nên hàm số đồng biến trên .
Do đó ta có:
, nên mệnh đề A sai.
nên mệnh đề B sai.
Mệnh đề C sai.
Vì nên mệnh đề D đúng.
Chọn D.
Câu 31:
Phương pháp:
Xét các trường hợp.
Cách giải:
Gọi số có 4 chữ số là .
Vì nên ta xét các TH sau:
TH1: .
Để Số có dạng .
. Mà , do đó .
Số có dạng .
Mà .
TH1 không có số nào thỏa mãn.
TH2: Có 2 cách chọn .
Khi đó số chắc chắn thỏa mãn nhỏ hơn 4012.
Có 4 cách chọn .
Số cách chọn 2 chữ số còn lại là cách.
có số.
TH3: Có 1 cách chọn .
Khi đó số chắc chắn thỏa mãn nhỏ hơn 4012.
Có 3 cách chọn .
Số cách chọn 2 chữ số còn lại là cách.
có số.
Vậy tổng có số.
Chọn D.
Câu 32:
Phương pháp:
- Tìm đạo hàm của phương trình quãng đường để suy ra v.
- Tìm vận tốc lớn nhất bằng cách sử dụng hằng đẳng thức.
Cách giải:
Ta có .
Ta có: .
Vậy .
Chọn C.
Câu 33:
Phương pháp:
Hàm số đạt cực đại tại .
Cách giải:
Ta có .
Để hàm số đạt cực đại tại thì qua điểm đạo hàm phải đổi dấu từ dương sang âm.
.
Chọn A.
Câu 34:
Phương pháp:
Áp dụng công thức tính nhân xác suất.
Cách giải:
Khi gieo hai con súc sắc trong một lần gieo thì có tất cả khả năng.
Ta có .
Xác suất để số chấm xuất hiện trên 2 con súc sắc bằng 6 là , xác suất để số chấm xuất hiện trên 2 con xúc xắc khác 6 là .
Vậy xác suất cần tìm là: .
Chọn D.
Câu 35:
Phương pháp:
Khai triển nhị thức Niton: .
Cách giải:
Ta có
Số hạng chứa trong khai triển ứng với .
Khi đó hệ số của bằng .
Chọn C.
Câu 36:
Phương pháp:
Áp dụng định nghĩa khối đa diện.
Cách giải:
Khối đa diện lồi có 10 đỉnh và 7 mặt thì áp dụng định lí ơle ta có
.
Chọn C.
Câu 37:
Phương pháp:
+) Xác định mặt phẳng đi qua và song song với BC.
+) Sử dụng công thức tỉ lệ thể tích Simpson: Choc chóp , . Khi đó .
Cách giải:
Trong qua kẻ . Khi đó mặt phẳng đi qua AG và song song với BC chính là mặt phẳng . Mặt phẳng này chia khối chóp thành 2 khối S.AMN và AMNBC.
Gọi là trung điểm của .
Vì Theo định lí Ta-lét ta có: .
.
Mà .
Ta có vuông cân tại .
.
Vậy .
Chọn A.
Câu 38:
Phương pháp:
Dựng hình và đổi điểm trong bài toán khoảng cách từ điểm đến mặt phẳng
Cách giải:
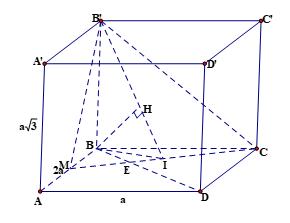
Gọi là trung điểm của (vì vuông cân).
Kẻ
Ta có tam giác vuông cân tại nên
Mặt khác gọi là giao điểm của và
Chọn D.
Câu 39:
Phương pháp:
Xác định chiều cao hình chóp
Thể tích khối chóp là với là chiều cao hình chóp và là diện tích đáy.
Cách giải:
Trong kẻ tại
Ta có
Xét tam giác SAH có
Thể tích khối chóp là
Chọn D.
Câu 40:
Phương pháp:
- Dựa vào định nghĩa để xác định các đường tiệm cận của đồ thị hàm số .
+ Đường thẳng là đường tiệm cận ngang của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: , .
+ Đường thẳng là đường tiệm cận đứng của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: , , , .
Cách giải:
Ta có:
Vậy đồ thị hàm số có hai đường tiệm cận ngang là .
Chọn C.
Câu 41:
Phương pháp:
Sử dụng công thức .
Cách giải:
Ta có .
Do .
Lại có
.
Ta có .
Vậy .
Chọn A.
Câu 42:
Phương pháp:
- Hai đồ thị hàm số và tiếp xúc với nhau khi và chỉ khi hệ phương trình có nghiệm.
- Nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số và .
Cách giải:
Đồ thị hàm số tiếp xúc với trục hoành tại gốc tọa độ.
có nghiệm .
Đồ thị hàm số cắt đường thẳng tại điểm có tung độ bằng 3 nên đồ thị hàm số đi qua điểm .
.
Vậy .
Chọn C.
Câu 43:
Phương pháp:
- Xác định hình chiếu của điểm B lên (SAC).
- Góc giữa SB và (SAC) là góc giữa SB và hình chiếu của SB lên (SAC).
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Cách giải:
Gọi .
Vì .
là hình chiếu của SB lên .
.
Vì ABCD là hình vuông cạnh 2a nên .
Áp dụng định lí Pytago trong tam giác vuông SAB ta có: .
Vì vuông tại .
.
Vậy .
Chọn D.
Câu 44:
Phương pháp:
Hai đường thẳng vuông góc với nhau khi và chỉ khi tích hệ số góc của hai đường thẳng đó bằng .
Cách giải:
Gọi là 2 điểm trên đồ thị hàm số sao cho từ tiếp tuyến tại A và tại B vuông góc với nhau. Khi đó:
: Vô lý, do
Vậy, không tồn tại tiếp điểm A, B thỏa mãn đề bài, suy ra, không tồn tại điểm mà từ đó kẻ được hai tiếp tuyến đến đồ thị hàm số sao cho hai tiếp tuyến này vuông góc với nhau.
Chọn A.
Câu 45:
Phương pháp:
So sánh chiều cao và diện tích đáy với hình lăng trụ.
Cách giải:
Ta có:
Tam giác cân tại có .
Áp dụng định lí Sin trong tam giác ta có: .
Ta có: .
.
Vậy .
Chọn A.
Câu 46:
Phương pháp:
+) Dùng công thức đạo hàm hàm hợp tính với
+) Hàm số nghịch biến trên và bằng 0 tại hữu hạn điểm.
Cách giải:
Dựa vào bảng xét dấu ta suy ra BBT của hàm số như sau:

.
Đặt .
Với Loại đáp án C và D.
Với Loại đáp án B.
Chọn A.
Câu 47:
Phương pháp:
- Phá trị tuyệt đối và giải phương trình.
- Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng song song với trục hoành.
Cách giải:
Ta có .
Dựa vào BBT ta có: .
Vậy phương trình ban đầu có 2 nghiệm phân biệt.
Chọn B.
Câu 48:
Phương pháp:
- Dựa vào định nghĩa để xác định các đường tiệm cận của đồ thị hàm số .
+ Đường thẳng là đường tiệm cận ngang của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: , .
+ Đường thẳng là đường tiệm cận đứng của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: , , , .
Cách giải:
Hàm số có ĐKXĐ: .
Ta có nhận đường thẳng làm tiệm cận đứng.
Ta lại có: nên đồ thị hàm số có tiệm cận ngang là .
Vậy đồ thị hàm số đã cho có tất cả 2 đường tiệm cận.
Chọn C.
Câu 49:
Phương pháp:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Gọi E là trung điểm của AD ta có ABCE là hình vuông và
Kẻ ta có
Ta có:
![]()
Xét tam giác SCD có vuông tại C.
Có vuông ở C.
Áp dụng định lí Cosin trong tam giác HCE:
Vậy .
Chọn A.
Câu 50:
Phương pháp:
- Hàm số nghịch biến trên .
- Cô lập , đưa bất phương trình về dạng .
- Lập BBT hàm số và kết luận.
Cách giải:
Hàm số đã cho xác định và liên tục trên .
Ta có: .
Để hàm số nghịch biến trên .
Xét hàm số trên ta có:
.
Hàm số đồng biến trên .
Do đó .
Vậy .
Chọn B.