Với giải bài tập Toán lớp 6 Bài 2: Tập hợp số tự nhiên. Ghi số tự nhiên chi tiết bám sát nội dung sgk Toán 6 Tập 1 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:

Giải bài tập Toán 6 Bài 2: Tập hợp số tự nhiên. Ghi số tự nhiên

Video giải Toán 6 Bài 2: Tập hợp số tự nhiên, Ghi số tự nhiên - Chân trời sáng tạo

A. Các câu hỏi trong bài

Giải Toán 6 trang 10 Tập 1 Chân trời sáng tạo

Hoạt động khởi động trang 10 Toán lớp 6 Tập 1: Bạn đã biết các số trên mặt đồng hồ này chưa?

Lời giải:

Nếu đã biết thì đây là các số La Mã.

Nếu chưa biết thì các số này sẽ được giới thiệu trong bài học ngày hôm nay.

Thực hành 1 trang 10 Toán lớp 6 Tập 1: a) Tập hợp N và N* có gì khác nhau?

b) Viết tập hợp sau bằng cách liệt kê các phần tử C = { a ∈ N*| a < 6 }.

Lời giải:

a) Tập hợp N = { 0;1;2;3;...}

Tập hợp N* = {1;2;3;4;...}

So với tập hợp N* thì tập hợp N có thêm số 0.

b) C = { a ∈ N*| a < 6 }.

Ta thấy tập hợp C bao gồm các phần tử là các số tự nhiên khác 0 và nhỏ hơn 6 là các số 1; 2; 3; 4; 5.

Theo cách liệt kê phần tử thì tập hợp C được viết dưới dạng: C = {1; 2; 3; 4; 5}.

Thực hành 2 trang 10 Toán lớp 6 Tập 1: Thay mỗi chữ cái dưới đây bằng một số tự nhiên phù hợp trong những trường hợp sau:

a) 17, a, b là ba số lẻ liên tiếp tăng dần;

b) m, 101, n, p là bốn số tự nhiên liên tiếp giảm dần.

Lời giải:

a) Các số tự nhiên lẻ liên tiếp hơn kém nhau 2 đơn vị. 

Vì 17, a, b là ba số lẻ liên tiếp tăng dần nên a = 19, b = 21.

Vậy a = 19, b = 21 ta có dãy các số là 17, 19, 21.

b) Các số tự nhiên liên tiếp hơn kém nhau 1 đơn vị.

Do đó m, 101, n, p là bốn số tự nhiên liên tiếp giảm dần nên m = 102, n = 100, p = 99.

Vậy m = 102, n = 100, p = 99 ta có dãy các số là 102, 101, 100, 99. 

Giải Toán 6 trang 11 Tập 1 Chân trời sáng tạo

Hoạt động khám phá trang 11 Toán lớp 6 Tập 1: So sánh a và 2020 trong các trường hợp sau:

a) a > 2 021               b) a < 2 000.

Lời giải:

a) Vì a > 2 021 mà 2 021 > 2 020 nên a > 2 020.

Vậy a > 2 020.

b) Vì a < 2 000  mà 2 000 < 2 020 nên a < 2 020.

Vậy a < 2 020.

Thực hành 3 trang 11 Toán lớp 6 Tập 1: Cho tập hợp A gồm các số tự nhiên có tận cùng là số 0 hoặc 5 và nhỏ hơn 36. Liệt kê các phần tử của A theo thứ tự giảm dần.

Lời giải:

Các số tự nhiên có tận cùng là số 0 hoặc 5 và nhỏ hơn 36 là: 0; 5; 10; 15; 20; 25; 30; 35.

Khi đó ta có:

Các phần tử của tập hợp A theo thứ tự giảm dần là: A = {0; 5; 10; 15; 20; 25; 30; 35}.

Thực hành 4 trang 11 Toán lớp 6 Tập 1: Mỗi số sau có bao nhiêu chữ số? Chỉ ra chữ số hàng đơn vị, hàng chục, hàng trăm, … của mỗi số đó.

2 023;    5 427 198 653.

Lời giải:

+) Số 2 023 có 4 chữ số, trong đó: 

- Chữ số hàng đơn vị: 3;

- Chữ số hàng chục: 2;

- Chữ số hàng trăm: 0;

- Chữ số hàng nghìn: 2.

+) Số 5 427 198 653 có 10 chữ số, trong đó:

- Chữ số hàng đơn vị: 3;

- Chữ số hàng chục: 5;

- Chữ số hàng trăm: 6;

- Chữ số hàng nghìn: 8;

- Chữ số hàng chục nghìn: 9;

- Chữ số hàng trăm nghìn: 1;

- Chữ số hàng triệu: 7;

- Chữ số hàng chục triệu: 2;

- Chữ số hàng trăm triệu: 4;

- Chữ số hàng tỉ: 5.

Thực hành 5 trang 11 Toán lớp 6 Tập 1: a) Dựa theo cách biểu diễn trên, hãy biểu diễn các số 345 và 2 021.

b) Đọc số 96 208 984. Số này có mấy chữ số? Số triệu, số trăm là bao nhiêu?

Lời giải:

a) Theo cấu tạo thập phân của một số, ta biểu diễn:

Số 345 có 3 trăm, 4 chục và 5 đơn vị, nghĩa là 

345 = 3 x 100 + 4 x 10 + 5.

Số 2 021 có 2 nghìn, 0 trăm, 2 chục và 1 đơn vị, nghĩa là

2 021 = 2 x 1 000 + 0 x 100 + 2 x 10 + 1.

b) - Cách đọc số 96 208 984 là: Chín mươi sáu triệu hai trăm linh tám nghìn chín trăm tám mươi tư.

- Số trên có 8 chữ số.

- Số triệu là 96; số trăm là 962 089.

Giải Toán 6 trang 12 Tập 1 Chân trời sáng tạo

Thực hành 6 trang 12 Toán lớp 6 Tập 1: Hoàn thành bảng dưới đây vào vở:

Số La Mã	XII		XXII					XXIV
Giá trị tương ứng trong hệ thập phân		20		17	30	26	28

Lời giải:

+) Giá trị tương ứng của số La Mã XII trong hệ thập phân là: 12.

+) Số La Mã biểu diễn cho số 20 là XX.

+) Giá trị tương ứng của số La Mã XXII trong hệ thập phân là: 22.

+) Số La Mã biểu diễn cho số 17 là: XVII.

+) Số La Mã biểu diễn cho số 30 là: XXX.

+) Số La Mã biểu diễn cho số 26 là: XXVI.

+) Số La Mã biểu diễn cho số 28 là: XXVIII.

+) Giá trị tương ứng của số La Mã XXIV trong hệ thập phân là 24.

Ta hoàn thành bảng đã cho: 

Số La Mã	XII	XX	XXII	XVII	XXX	XXVI	XXVIII	XXIV
Giá trị tương ứng trong hệ thập phân	12	20	22	17	30	26	28	24

B. Bài tập

Bài 1 trang 12 Toán lớp 6 Tập 1: Chọn kí hiệu thuộc (∈) hoặc không thuộc (∉) thay cho mỗi ?.

 

 

 

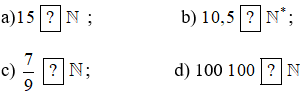
Lời giải:

Tập hợp là tập hợp các số tự nhiên: N = {0; 1; 2; 3; 4; 5; …}.

Tập hợp là tập hợp các số tự nhiên khác 0: N* = {1; 2; 3; 4; 5; 6; …}.

Do đó: 

a) 15 là số tự nhiên nên 15 thuộc tập hợp N, ta viết 15 ∈ N .

b) Số 10,5 không phải là số tự nhiên nên 10,5 không thuộc tập hợp N*, ta viết  10,5 ∉ N*.

c) Số 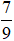 không phải là số tự nhiên nên  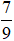không thuộc tập hợp N, ta viết  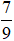∉ N.

d) Số 100 là số tự nhiên nên 100 thuộc tập hợp N nên ta viết 100 ∈ N.

Bài 2 trang 12 Toán lớp 6 Tập 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

a) 1 999 > 2 003;

b) 100 000 là số tự nhiên lớn nhất;

c) 5 ≤ 5;

d) Số 1 là số tự nhiên nhỏ nhất.

Lời giải:

a) Ta thấy 1 999 < 2 003 nên khẳng định 1999 > 2003 là sai.

b) Ta có: 100 001 > 100 000 

Mà 100 001 cũng là một số tự nhiên

Nên khẳng định 100 000 là số tự nhiên lớn nhất là sai.

c) Ta có 5 = 5 nên khẳng định 5 ≤ 5 là đúng.

d) Ta có 0 < 1 

Mà 0 cũng là một số tự nhiên

Nên khẳng định 1 là số tự nhiên nhỏ nhất là sai.

Bài 3 trang 12 Toán lớp 6 Tập 1: Biểu diễn các số 1 983; 2 756; 2 053 theo mẫu 1 983 = 1 x 1000 + 9 x 100 + 8 x 10 + 3.

Lời giải:

+) 1 983 = 1 x 1000 + 9 x 100 + 8 x 10 + 3.

+) 2 756 = 2 x 1000 + 7 x 100 + 5 x 10 + 6.

+) 2 053 = 2 x 1000 + 0 x 100 + 5 x 10 + 3.

Bài 4 trang 12 Toán lớp 6 Tập 1: Hoàn thành bảng dưới đây vào vở.

Số tự nhiên	27		19		16
Số La Mã		XIV		XXIX

Lời giải:

Số La Mã biểu diễn cho số tự nhiên 27 là: XXVII.

Số tự nhiên biểu diễn cho số La Mã XIV là: 14.

Số La Mã biểu diễn cho số tự nhiên 19 là: XIX.

Số tự nhiên biểu diễn cho số La Mã XXIX là: 29.

Số La Mã biểu diễn cho số tự nhiên 16 là: XVI.

Ta hoàn thành bảng:

Số tự nhiên	27	14	19	29	16
Số La Mã	XXVII	XIV	XIX	XXIX	XVI

Lý thuyết Tập hợp số tự nhiên, Ghi số tự nhiên

1. Tập hợp $\mathrm{\mathbb{N}}$ và $\mathrm{\mathbb{N}}*$

Các số 0; 1; 2; 3; 4; ... là các số tự nhiên.

Tập hợp các số tự nhiên được kí hiệu là ℕ , tức là ℕ  = {0; 1; 2; 3; ...}.

Tập hợp các số tự nhiên khác 0 được kí hiệu là ℕ* , tức là  = ℕ* {1; 2; 3; ...}

Tập hợp $\mathrm{\mathbb{N}}$ bỏ đi số 0 thì được $\mathrm{\mathbb{N}}*$ .

Khi cho một số tự nhiên x ∈  ℕ*  thì ta hiểu x là số tự nhiên khác 0.

Ví dụ: Viết tập hợp sau bằng cách liệt kê các phần tử:

$A=\{a\in \mathbb{N}*|a<4\}$.

Hướng dẫn giải

Vì a $\in \mathrm{\mathbb{N}}*$  nên a là các số tự nhiên: 1; 2; 3; 4; 5; 6; ...

Tuy nhiên thêm điều kiện a < 4 nên a là các số 1; 2; 3.

Vậy tập hợp A được viết bằng cách liệt kê các phần tử A = {1; 2; 3}.

2. Thứ tự trong tập hợp số tự nhiên

a) Biểu diễn các số tự nhiên trên tia số:

Các số tự nhiên được biểu diễn trên tia số bởi các điểm cách đều như sau:

- Tia số có mũi tên sang phải biểu thị chiều tăng dần của các số tự nhiên.

- Mỗi số tự nhiên được biểu diễn bằng một điểm trên tia số; điểm biểu diễn số tự nhiên n được gọi là điểm n.

- Điểm 0 được gọi là gốc.

b) So sánh hai số tự nhiên

- Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết a < b (đọc là a nhỏ hơn b) hoặc b > a (đọc là b lớn hơn a).

- Khi biểu diễn trên tia số nằm ngang có chiều từ trái sang phải, nếu a < b thì điểm a nằm bên trái điểm b.

Ngoài ra ta cũng viết a ≥ b để chỉ a > b hoặc a = b.

+ Nếu a < b và b < c thì a < c (Tính chất bắc cầu).

+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.

+ Số 0 là số tự nhiên bé nhất.

Ví dụ:

- Số 3 và số 4 là hai số tự nhiên liên tiếp.

- Số liền sau của 89 là 90.

- Số liền trước của 16 là 15.

3. Ghi số tự nhiên

a) Cách ghi số tự nhiên trong hệ thập phân

Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.

Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó.

Ví dụ:

+ 10 chục thì bằng 1 trăm;

+ 10 trăm thì bằng 1 nghìn.

Chú ý: Khi viết các số tự nhiên, ta quy ước:

- Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.

- Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.

- Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau.

b) Hệ thập phân

Ta đã biết cấu tạo thập phân của một số:

- Kí hiệu 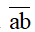 chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a (a ≠ 0) và chữ số hàng đơn vị là b.

Ta có: 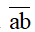 = a × 10 + b.

- Kí hiệu 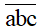 chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là a (a ≠ 0), chữ số hàng chục là b, chữ số hàng đơn vị là c.

Ta có: 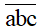  = a × 100 + b × 10 + c.

- Với các số cụ thể thì không viết dấu gạch ngang ở trên.

Ví dụ:

 = a × 100 + 5 × 10 + b (a ≠ 0).

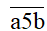
425 = 4 ×100 + 2 × 10 + 5.

c) Hệ La Mã

Cách ghi số La Mã như sau:

Chữ số	I	V	X
Giá trị tương ứng trong hệ thập phân	1	5	10

Ghép các chữ số I, V, X với nhau ta có thể được số mới. Dưới đây là bảng chuyển đổi La Mã sang số trong hệ thập phân tương ứng (từ 1 đến 10):

Số La Mã	I	II	III	IV	V	VI	VII	VIII	IX	X
Giá trị tương ứng trong hệ thập phân	1	2	3	4	5	6	7	8	9	10

Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X

XI	XII	XIII	XIV	XV	XVI	XVII	XVIII	XIX	XX
11	12	13	14	15	16	17	18	19	20

Các số La Mã biểu diễn các số từ 21 đến 30: Thêm XX vào bên trái mỗi số từ I đến X

Chú ý:

- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.

- Không có số La Mã nào biểu diễn số 0.

Ví dụ:

a) Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10; 1; 1; 1.

Ta có 10 + 1 + 1 + 1 = 13.

Do đó số XIII biểu diễn số 13.

b) Viết số 17 thành số La Mã như sau:

Số 7 được viết là VII.

Số 17 = 7 + 10, tức là số 7 thêm 10 đơn vị nên ta thêm X trước VII được XVII.

Do đó số 17 được viết thành số La Mã là XVII.

Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Tập hợp, Phần tử của tập hợp

Bài 3: Các phép tính trong tập hợp số tự nhiên

Bài 4: Lũy thừa với số mũ tự nhiên

Bài 5: Thứ tự thực hiện các phép tính