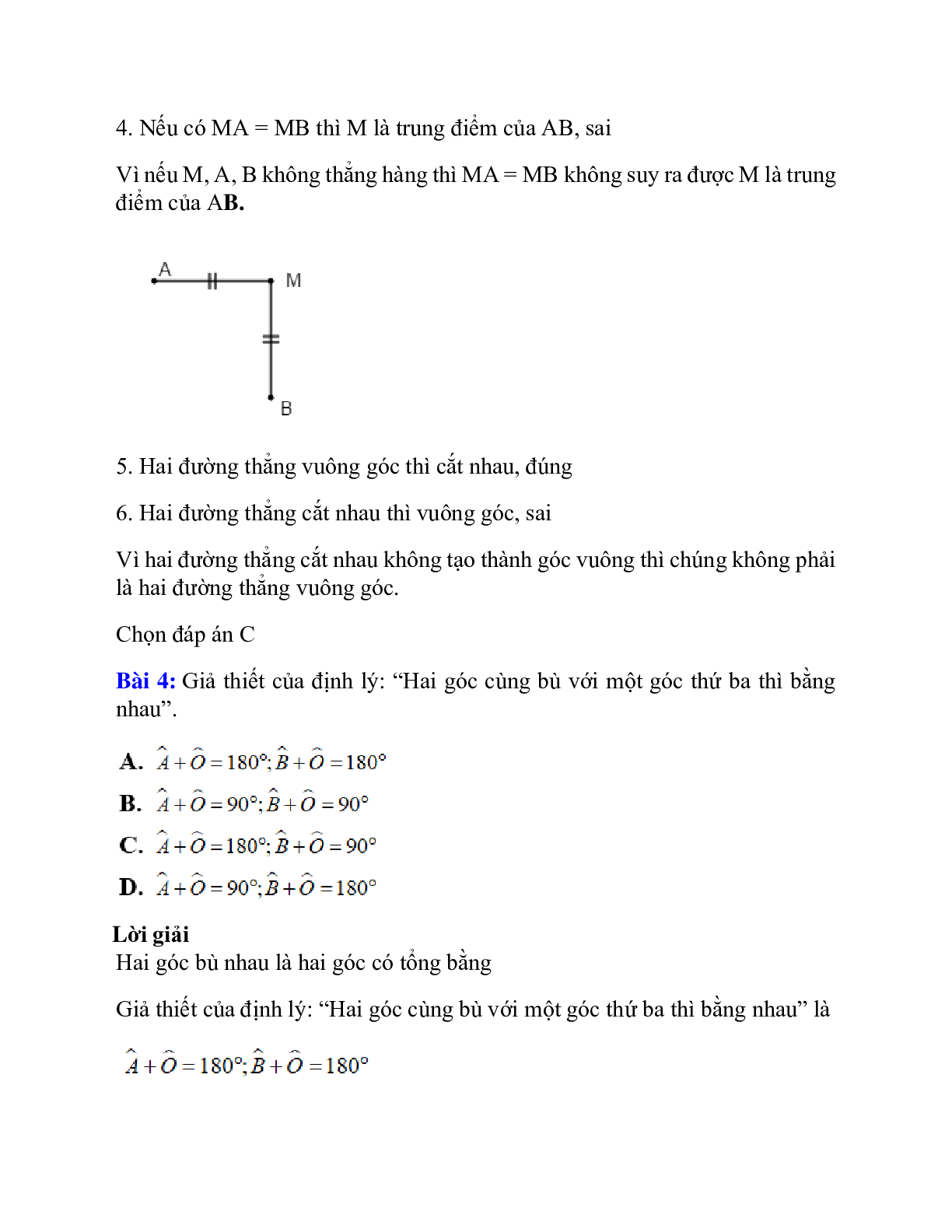Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 7: Định lí có đáp án chi tiết, chọn lọc. Tài liệu có 7 trang gồm 10 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 7. Hi vọng với bộ câu hỏi trắc nghiệm Định lí có đáp án này sẽ giúp bạn ôn luyện kiến thức để đạt kết quả cao trong bài thi môn Toán 7 sắp tới.

Giới thiệu về tài liệu:

- Số trang: 7 trang

- Số câu hỏi trắc nghiệm: 10 câu

- Lời giải & đáp án: có

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Định lí có đáp án – Toán lớp 7:

TRẮC NGHIỆM TOÁN 7

Bài 7: Định lí

Bài 1: Khi chứng minh định lý, người ta cần:

A. Chứng minh định lý đó đúng trong một trường hợp cụ thể của giả thiết

B. Chứng minh định lý đó đúng trong hai trường hợp cụ thể của giả thiết

C. Chứng minh định lý đó đúng trong mọi trường hợp có thể xảy ra của giả thiết

D. Chứng minh định lý đó đúng trong vài trường hợp cụ thể của giả thiết

Lời giải

Khi chứng minh định lý, ta cần chứng minh định lý đó đúng trong mọi trường hợp có thể xảy ra của giả thiết.

Chọn đáp án C

Bài 2: Phát biểu định lý sau bằng lời:

A. Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.

B. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.

C. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.

D. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.

Lời giải

Phát biểu định lý bằng lời: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.

Chọn đáp án B

Bài 3: Cho các định lý sau, có bao nhiêu định lý đúng

1. Hai góc đối đỉnh thì bằng nhau

2. Hai góc bằng nhau thì đối đỉnh

3. Nếu M là trung điểm của AB thì MA = MB

4. Nếu có MA = MB thì M là trung điểm của AB

5. Hai đường thẳng vuông góc thì cắt nhau

6. Hai đường thẳng cắt nhau thì vuông góc

A. 1

B. 2

C. 3

D. 6

Lời giải

1. Hai góc đối đỉnh thì bằng nhau, đúng

2. Hai góc bằng nhau thì đối đỉnh, sai

Vì tồn tại hai góc bằng nhau mà không chung đỉnh thì đó không phải hai góc đối đỉnh như hình sau:

3. Nếu M là trung điểm của AB thì MA = MB, đúng

4. Nếu có MA = MB thì M là trung điểm của AB, sai

Vì nếu M, A, B không thẳng hàng thì MA = MB không suy ra được M là trung điểm của AB.

5. Hai đường thẳng vuông góc thì cắt nhau, đúng

6. Hai đường thẳng cắt nhau thì vuông góc, sai

Vì hai đường thẳng cắt nhau không tạo thành góc vuông thì chúng không phải là hai đường thẳng vuông góc.

Chọn đáp án C

Bài 4: Giả thiết của định lý: “Hai góc cùng bù với một góc thứ ba thì bằng nhau”.

Chọn đáp án A

Bài 5: Chọn câu đúng:

A. Giả thiết của định lý là điều cho biết

B. Kết luận của định lý là điều được suy ra

C. Người ta dùng lập luận để từ giả thiết suy ra kết luận của định lý

D. Cả A, B, C đều đúng

Lời giải

Từ phần lý thuyết ta có:

Giả thiết của định lý là điều cho biết

Kết luận của định lý là điều được suy ra

Người ta dùng lập luận để từ giả thiết suy ra kết luận của định lý

Suy ra cả A, B, C đều đúng.

Chọn đáp án D

Bài 6: Chứng minh định lý là:

A. Dùng lập luận để từ giả thiết suy ra kết luận

B. Dùng hình vẽ để từ giả thiết suy ra kết luận

C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận

D. Cả A, B, C đều sai

Lời giải

Chứng minh định lý là dùng lập luận để từ giả thiết suy ra kết luận

Chọn đáp án A.

Bài 7: Trong các câu sau, câu nào cho một định lý:

A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.

C. Nếu hai đường thẳng và cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.

D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.

Lời giải

Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”

Chọn đáp án A.

Bài 8: Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là:

Lời giải

Giả thiết của định lý trên là: a // b, c ∩ a = {A}, c ∩ b = {B}

Chọn đáp án B.

Bài 9: Chọn định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:

A. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OE ⊥ OF

B. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOF, OF là phân giác góc AOD. Kết luận: OE ⊥ OA

C. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOE. Kết luận: OE ⊥ OF

D. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OB ⊥ OF

Lời giải

Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD.

Kết luận: OE ⊥ OF

Chọn đáp án A.

Bài 10: Phần giả thiết:(tham khảo hình vẽ) là của định lý nào dưới đây:

A. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc ngoài cùng phía bù nhau thì hai đường thẳng đó song song.

B. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song.

C. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.

D. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.

Lời giải

Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.

Chọn đáp án D.