Trong không gian Oxyz, cho hai điểm A(2; 4; 1); B(-1; 1; 3) và mặt phẳng (P): x - 3y + 2z - 5 = 0. Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình dạng ax + by + cz - 11 = 0. Khi đó a + b + c bằng
A. 5;
B. 15;
C. -5;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Ta có: và
Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) nên suy ra véc-tơ pháp tuyến của (Q) vuông góc với véc-tơ pháp tuyến của (P) và véc-tơ
= (0; -8; -12) = (0; 2; 3)
Phương trình mặt phẳng (Q) đi qua điểm B và nhận (0; 2; 3) làm véc-tơ pháp tuyến là
(Q): 2.(y - 1) + 3.(z - 3) = 0
Û 2y + 3z - 11 = 0
Mà ta có: (Q) có phương trình dạng ax + by + cz - 11 = 0 nên suy ra a = 0, b = 2, c = 3
Khi đó a + b + c = 0 + 2 + 3 = 5.
Lý thuyết Vectơ pháp tuyến của mặt phẳng:
• Vectơ n→ ≠ 0→ là vectơ pháp tuyến (VTPT) nếu giá của n→ vuông góc với mặt phẳng (α)
• Chú ý:
- Nếu n→ là một VTPT của mặt phẳng (α) thì kn→ cũng là một VTPT của mặt phẳng (α).
- Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.
- Nếu u→, v→ có giá song song hoặc nằm trên mặt phẳng (α) thì n→ = [u→, v→] là một VTPT của (α)
*Phương trình tổng quát của mặt phẳng
- Trong không gian Oxy , mọi mặt phẳng đều có dạng phương trình:
Ax + By + Cz + D = 0 với A2 + B2 + C2 ≠ 0
- Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là n→(A; B; C).
- Phương trình mặt phẳng đi qua điểm Mo(xo; yo; zo) và nhận vectơ n→(A; B; C) khác 0→ là VTPT là: A(x - xo) + B(y - yo) + C(z - zo) = 0 .
Bài tập liên quan:
Gọi S là tập hợp tất cả các số phức z sao cho số phức có phần thực bằng . Xét các số phức z1, z2 Î S thỏa mãn |z1 - z2| = 6, giá trị nhỏ nhất của P = |z1 - 10|2 - |z2 - 10|2 bằng
A. -192;
B. -120;
C. -256;
D. -60.
Cách giải:
Đáp án đúng là: B
Gọi z = a + bi
Điều kiện |z| - z ¹ 0 Þ b ¹ 0
w có phần thực là nên suy ra
Xét các số phức z1, z2 Î S thỏa mãn |z1 - z2| = 6 nên suy ra
Þ (a1 - a2)2 + (b1 - b2)2 = 36
Ta có:
P = |z1 - 10|2 - |z2 - 10|2
= (a1 - 10)2 + b12 - (a2 - 10)2 - b22
= a12 - a22 - 20(a1 - a2) + b12 - b22
= - 20(a1 - a2)
Þ P ³ - 20|a1 - a2|
Để P đạt GTNN thì đạt GTLN nên suy ra b1 = b2
Vậy GTNN của P là
Tham khảo thêm một số tài liệu liên quan:
Diện tích hình phẳng giới hạn bởi hai đường y = x2 - 4 và y = 2x - 4 bằng
Cho hàm số y = f (x) có đạo hàm là f '(x) = 12x2 + 2, x ℝ và f (-1) = 3. Biết F (x) là nguyên hàm của f (x) thỏa mãn F (-2) = 2, khi đó F (1) bằng
Trong không gian Oxyz, tọa độ một vectơ vuông góc với cả hai vectơ và là
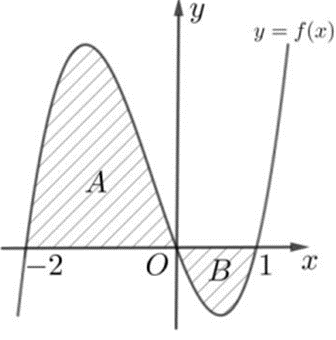
Cho hàm số y = f (x) có đồ thị như hình vẽ và diện tích hai phần A; B lần lượt bằng 11; 2. Giá trị của bằng
Trong không gian Oxyz, cho hai điểm A(-2; 3; 1) và B(5; 6; 2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tỉ số bằng
Phương trình z2 + a.z + b = 0, với a, b là các số thực nhận số phức 1 - i là một nghiệm. Khi đó a - b bằng
Trong không gian Oxyz, cho mặt phẳng (Q) song với mặt phẳng (P): 2x - 2y + z - 7 = 0. Biết mặt phẳng (Q) cắt mặt cầu (S): x2 + (y - 2)2 + (z + 1)2 = 25 theo một đường tròn có bán kính r = 3. Khi đó mặt phẳng (Q) có phương trình là
Trong không gian Oxyz , cho hai điểm A(1; 1; 2), B(-1; 3; -9). Tọa độ điểm M thuộc Oy sao cho DABM vuông tại A là
Trong không gian Oxyz, cho 4 điểm A(2; 0; 2), B(1; -1; -2), C(-1;1 ; 0), D(-2; 1; 2). Thể tích của khối tứ diện ABCD bằng