Trong không gian Oxyz, cho hai điểm A(-2; 3; 1) và B(5; 6; 2). Đường thẳng AB cắt mặt phẳng (Oxz)...

Question

Trong không gian Oxyz, cho hai điểm A(-2; 3; 1) và B(5; 6; 2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tỉ số AMBM bằng

VietJack · Accepted Answer

Đáp án đúng là: A Ta có: AB→=7; 3; 1 Phương trình tham số của đường thẳng AB đi qua A(-2; 3; 1) nhận AB→=7; 3; 1 làm véc-tơ chỉ phương là AB:x=−2+7ty=3+3t z=1+t Gọi M là giao điểm của AB và mặt phẳng (Oxz) nên suy ra M(a; 0; b) thuộc AB ⇒a=−2+7t0=3+3t b=1+t ⇔a=−2−7t=−1 b=1−1 ⇔a=−9t=−1b=0 Từ đó suy ra M(-9; 0; 0) Vậy ta có: +) AM=(−9+2)2+(−3)2+(−1)2=59 +) BM=(−9−5)2+(−6)2+(−2)2=259 Từ đó suy ra được tỉ số AMBM=59259=12.

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Trong không gian Oxyz, cho hai điểm A(-2; 3; 1) và B(5; 6; 2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tỉ số $\frac{A M}{B M}$ bằng

A. $\frac{1}{2};$

B. 2;

C. $\frac{1}{3};$

D. 3.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Trong không gian Oxyz, đường thẳng $d : \{\begin{matrix} x = 1 + 2 t \\ y = 2 - 2 t \\ z = - 3 - 3 t \end{matrix}$ đi qua điểm nào dưới đây?

Câu 2:

Diện tích hình phẳng giới hạn bởi hai đường y = x² - 4 và y = 2x - 4 bằng

Câu 3:

Cho hàm số y = f (x) có đạo hàm là f '(x) = 12x² + 2, x $\in$ ℝ và f (-1) = 3. Biết F (x) là nguyên hàm của f (x) thỏa mãn F (-2) = 2, khi đó F (1) bằng

Câu 4:

Trong không gian Oxyz, cho hai điểm A(2; 4; 1); B(-1; 1; 3) và mặt phẳng (P): x - 3y + 2z - 5 = 0. Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình dạng ax + by + cz - 11 = 0. Khi đó a + b + c bằng

Câu 5:

Trong không gian Oxyz, tọa độ một vectơ vuông góc với cả hai vectơ $\vec{a} = (1; 1; - 2)$ và $\vec{b} = (3; - 2; - 1)$ là

Câu 6:

Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2x - x² và y = 0. Vật thể tròn xoay được sinh ra bởi hình phẳng (H) khi nó quay quanh trục Ox có thể tích bằng

Câu 7:

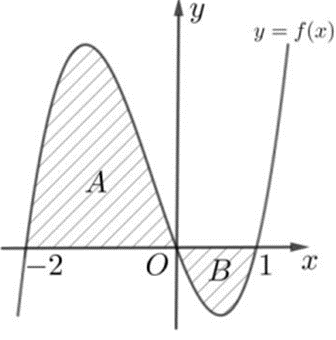
Cho hàm số y = f (x) có đồ thị như hình vẽ và diện tích hai phần A; B lần lượt bằng 11; 2. Giá trị của $I = \int_{- 1}^{0} f (3 x + 1) d x$ bằng

Câu 8:

Trên khoảng (0; +¥), họ nguyên hàm của hàm số $f (x) = x^{\frac{5}{2}}$ là:

Câu 9:

Trên mặt phẳng tọa độ, cho M (2; -3) là điểm biểu diễn của số phức z. Phần ảo của z bằng

Câu 10:

Phương trình z² + a.z + b = 0, với a, b là các số thực nhận số phức 1 - i là một nghiệm. Khi đó a - b bằng

Câu 11:

Trong không gian Oxyz, cho mặt phẳng (Q) song với mặt phẳng (P): 2x - 2y + z - 7 = 0. Biết mặt phẳng (Q) cắt mặt cầu (S): x² + (y - 2)² + (z + 1)² = 25 theo một đường tròn có bán kính r = 3. Khi đó mặt phẳng (Q) có phương trình là

Câu 12:

Trong không gian Oxyz , cho hai điểm A(1; 1; 2), B(-1; 3; -9). Tọa độ điểm M thuộc Oy sao cho DABM vuông tại A là

Câu 13:

Trong không gian Oxyz, cho 4 điểm A(2; 0; 2), B(1; -1; -2), C(-1;1 ; 0), D(-2; 1; 2). Thể tích của khối tứ diện ABCD bằng

Câu 14:

Cho hàm số f (x) = x + cos x. Khẳng định nào dưới đây đúng?

Đề thi liên quan

Câu hỏi mới nhất