Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2x - x² và y = 0. Vật thể tròn xoay được sinh ra bởi hình phẳng (H) khi nó quay quanh trục Ox có thể tích bằng

Trong không gian Oxyz, đường thẳng $d:\left\{\begin{array}{c}x=1+2t\\ y=2-2t\\ z=-3-3t\end{array}\right.$ đi qua điểm nào dưới đây?

Cho hàm số y = f (x) có đạo hàm là f '(x) = 12x² + 2, x $\in$ ℝ và f (-1) = 3. Biết F (x) là nguyên hàm của f (x) thỏa mãn F (-2) = 2, khi đó F (1) bằng

Trong không gian Oxyz, cho hai điểm A(2; 4; 1); B(-1; 1; 3) và mặt phẳng (P): x - 3y + 2z - 5 = 0. Một mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình dạng ax + by + cz - 11 = 0. Khi đó a + b + c bằng

Trong không gian Oxyz, tọa độ một vectơ vuông góc với cả hai vectơ $\overrightarrow{a}=\left(1;1;-2\right)$ và $\overrightarrow{b}=\left(3;-2;\text{\hspace{0.33em}}-1\right)$  là

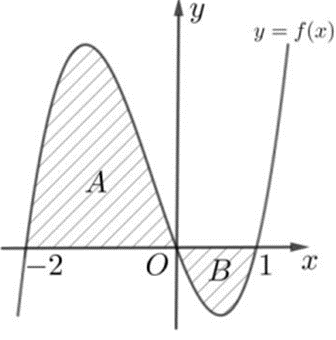
Cho hàm số y = f (x) có đồ thị như hình vẽ và diện tích hai phần A; B lần lượt bằng 11; 2. Giá trị của $I=\underset{-1}{\overset{0}{\int }}f\left(3x+1\right)dx$ bằng

Trong không gian Oxyz, cho hai điểm A(-2; 3; 1) và B(5; 6; 2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tỉ số $\frac{AM}{BM}$  bằng

Phương trình z² + a.z + b = 0, với a, b là các số thực nhận số phức 1 - i là một nghiệm. Khi đó a - b bằng

Trong không gian Oxyz, cho mặt phẳng (Q) song với mặt phẳng (P): 2x - 2y + z - 7 = 0. Biết mặt phẳng (Q) cắt mặt cầu (S): x² + (y - 2)² + (z + 1)² = 25  theo một đường tròn có bán kính r = 3. Khi đó mặt phẳng (Q) có phương trình là

Trong không gian Oxyz , cho hai điểm A(1; 1; 2), B(-1; 3; -9). Tọa độ điểm M thuộc Oy sao cho DABM vuông tại A là

Trong không gian Oxyz, cho 4 điểm A(2; 0; 2), B(1; -1; -2), C(-1;1 ; 0), D(-2; 1; 2). Thể tích của khối tứ diện ABCD bằng

Cho hàm số f (x) = x + cos x. Khẳng định nào dưới đây đúng?