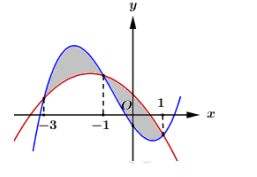
Tập nghiệm của bất phương trình log4(x + 7) log2(x + 1) là...

Question

Tập nghiệm của bất phương trình log4x+7>log2x+1 là khoảng (a; b). Giá trị M=2a−b bằng

VietJack · Accepted Answer

Chọn D. Phương pháp: - Tìm ĐKXĐ. - Đưa về cùng cơ số. - Giải bất phương trình logarit: logax>logay⇔x>ya>1. Cách giải: ĐKXĐ: x+7>0x+1>0⇔x>−7x>−1⇔x>−1. Ta có log4x+7>log2x+1 ⇔log4x+7>log4x+12 ⇔x+7>x+12 ⇔x2+x−6<0 ⇔−3 b; logaf(x) ≥ b; logaf(x) < b; logaf(x) ≤ b Phương pháp đưa về cùng cơ số Xét bất phương trình logaf(x) > logag(x) (a > 0, a ≠ 1) • Nếu a > 1 thì logaf(x) > logag(x) ⇔ f(x) > g(x) (cùng chiều khi a > 1) • Nếu 0 < a < 1 thì logaf(x) > logag(x) ⇔ f(x) < g(x) (ngược chiều khi 0 < a < 1 ) • Nếu a chứa ẩn thì logaf(x) > logag(x) ⇔ 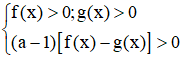(hoặc chia 2 trường hợp của cơ số) Bài tập liên quan: Biết tập nghiệm của bất phương trình 2x<3-22x là khoảng (a;b), Giá trị a+b là A. 3 B. 2 C. 0 D. 1 Cách giải: Tham khảo thêm một số tài liệu liên quan: Đề thi thử Toán sở GD&ĐT Hà Tĩnh năm 2024 Đề thi thử Toán sở GD&ĐT Lạng Sơn năm 2024

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Tập nghiệm của bất phương trình $\log_{4} (x + 7) > \log_{2} (x + 1)$ là khoảng (a; b). Giá trị $M = 2 a - b$ bằng

A. 8

B. 0

C. 4

D. -4

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho $I = \int_{1}^{e} \frac{\ln x}{x {(\ln x + 2)}^{2}} d x = a \ln 3 + b \ln 2 + \frac{c}{3}$ với $a, b, c \in ℤ .$ Giá trị $a^{2} + b^{2} + c^{2}$ bằng

Câu 2:

Tam giác ABC vuông cân đỉnh A có cạnh huyền là $\sqrt{2}$ . Quay tam giác ABC quanh trục AB được khối nón có thể tích là

Câu 3:

Cho hình chóp tứ giác S.ABCD có đáy là hình vuông, mặt bên (SAB) là đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng (SCD) bằng $\frac{3 \sqrt{7} a}{7} .$ Thể tích khối chóp S.ABCD là

Câu 4:

Cho hình chóp S.ABC có tam giác ABC vuông tại $A, A B = 2 a, A C = a, S A = 3 a; S A ⊥ (A B C) .$ Thể tích hình chóp là:

Câu 5:

Số phức z thỏa mãn $(1 - i) z + i = 0$ là

Câu 6:

Tập xác định của hàm số $y = {(x - 1)}^{- 2}$ là

Câu 7:

Họ tất cả các nguyên hàm của hàm số $y = e^{x} + \cos x$ là

Câu 8:

Câu 9:

Nghiệm phức có phần ảo dương của phương trình $z^{2} + 2 z + 5 = 0$ là

Câu 10:

Với a là số thực dương tùy ý, $\log_{2} (2 a^{2})$ bằng

Câu 11:

Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng

Câu 12:

Số giao điểm của đường thẳng y = x + 1 và đồ thị hàm số $y = x^{3} - 3 x + 1$ là:

Câu 13:

Cho hàm số $f (x) = \frac{2 x - m}{x + 2}$ (m là tham số). Để $\min_{x \in [- 1; 1]} f (x) = \frac{1}{3}$ thì $m = \frac{a}{b} (a \in ℤ, b \in ℕ, b > 0) .$ Tổng a + b bằng

Câu 14:

Phương trình $\log_{5} (2 x - 3) = 1$ có nghiệm là

Đề thi liên quan

Câu hỏi mới nhất