Dựa vào đồ thị (C), biện luận số nghiệm phương trình sau theo m: x^3 + 3x^2 + 1 = m/2...

Question

Dựa vào đồ thị (C), biện luận số nghiệm phương trình sau theo m: x3+3x2+1=m2

VietJack · Accepted Answer

Số nghiệm của phương trình x3+3x2+1=m2 bằng số giao điểm của đồ thị (C) và đường thẳng y = m/2.Từ đồ thị ta có:+ Đường thẳng cắt đồ thị tại 1 điểm khi và chỉ khi :⇒ phương trình có 1 nghiệm.+ Để đường thẳng cắt đồ thị tại 2 điểm phân biệt khi và chỉ khi :⇒ Phương trình có hai nghiệm.+ Với 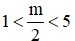⇔ 2 < m < 10.⇒ Đường thẳng cắt đồ thị hàm số tại 3 điểm⇒ Phương trình có ba nghiệm phân biệt.

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Dựa vào đồ thị (C), biện luận số nghiệm phương trình sau theo m: $x^{3} + 3 x^{2} + 1 = \frac{m}{2}$

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = x^{3} + 3 x^{2} + 1$

Câu 2:

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số $y = \frac{x + 3}{x + 1}$

Câu 3:

Cho hàm số: $f (x) = x^{3} - 3 m x^{2} + 3 (2 m - 1) + 1$ (m là tham số).
Xác định m để hàm số đồng biến trên tập xác định.

Câu 4:

Biện luận theo tham số m số nghiệm của phương trình: $x^{4} - 6 x^{2} + 3 = m$ .

Câu 5:

Cho hàm số $y = \frac{m x - 1}{2 x + m}$
Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên khoảng xác định của nó.

Câu 6:

Cho hàm số $y = \frac{1}{4} x^{4} + \frac{1}{2} x^{2} + m$
Viết phương trình tiếp tuyến (C) tại điểm có tung độ bằng 7/4.

Câu 7:

Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị (C).

Câu 8:

Cho hàm số $y = \frac{m x - 1}{2 x + m}$
Xác định m để tiệm cận đứng của đồ thị đi qua A(-1, $\sqrt{2}$ )

Câu 9:

Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số: $y = x^{4} - 2 x^{2} + 2$

Câu 10:

Cho hàm số $y = \frac{1}{4} x^{4} + \frac{1}{2} x^{2} + m$
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.

Câu 11:

Cho hàm số
$f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 4 x + 6$
Giải phương trình f'(sin x) = 0.

Câu 12:

Cho hàm số $y = 2 x^{2} + 2 m x + m - 1$ có đồ thị là $(C_{m})$ , m là tham số.
Chứng minh rằng $(C_{m})$ luôn cắt trục hoành tại hai điểm phân biệt với mọi m.

Câu 13:

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: $f (x) = - x^{3} + 3 x^{2} + 9 x + 2$

Câu 14:

Chứng minh rằng với mọi giá trị của đường thẳng y = 2x + m luôn cắt (C) tại hai điểm phân biệt M và N.

Đề thi liên quan

Câu hỏi mới nhất