Với Giải Toán lớp 6 trang 43 Tập 1 Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6. Mời các bạn đón xem:

Giải Toán lớp 6 trang 43 Tập 1 Kết nối tri thức

Bài 2.25 trang 43 Toán lớp 6 Tập 1: Từ các số 5, 0, 1, 3, viết các số tự nhiên có ba chữ số khác nhau thỏa mãn điều kiện:

a) Các số đó chia hết cho 5;

b) Các số đó chia hết cho 3.

Lời giải:

a) Gọi số tự nhiên cần tìm có ba chữ số khác nhau là  

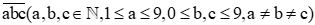
Vì số đó chia hết cho 5 nên chữ số tận cùng là 0 hoặc 5. Do đó c = 0 hoặc c = 5.

+) Với c = 0, ta có bảng chữ số a, b khác nhau và khác 0 thỏa mãn là:

Do đó ta thu được các số: 150; 510; 350; 530; 130; 310.

+) Với c = 5, a   0 nên a = 1 hoặc 3, ta có bảng chữ số a, b khác nhau thỏa mãn là:

Do đó ta thu được các số: 105; 305; 135; 315

Vậy các số tự nhiên có ba chữ số khac nhau chia hết cho 5 được viết từ các chữ số đã cho: 130; 135; 105; 150; 310; 315; 350; 305; 510; 530.

b) Gọi số tự nhiên cần tìm có ba chữ số khác nhau là  

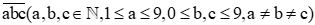
Vì số đó chia hết cho 3 nên tổng các chữ số của nó phải chia hết cho 3 hay (a + b + c) chia hết cho 3.

Ta thấy cặp 3 chữ số khác nhau có tổng chia hết cho 3 là: (5, 0, 1); (5, 1, 3) vì (5 + 0 + 1 = 6 chia hết cho 3 và 5 + 1 + 3 = 9 chia hết cho 3)

+) Với (5, 0, 1) ta có các số cần tìm là: 105; 150; 510; 501

+) Với (5, 1, 3) ta có các số cần tìm là: 135; 153; 351; 315; 513; 531

Vậy các số tự nhiên có ba chữ số khac nhau chia hết cho 3 được viết từ các chữ số đã cho: 135; 153; 351; 315; 513; 531; 105; 150; 510; 501.

Bài 2.26 trang 43 Toán lớp 6 Tập 1: Hãy phân tích các số A, B ra thừa số nguyên tố:

                A = 4².6³

                B = 9².15²

Lời giải:

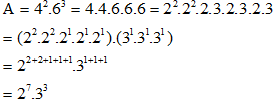
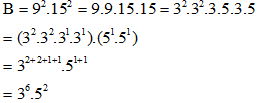
Bài 2.27 trang 43 Toán lớp 6 Tập 1: Tìm số tự nhiên x không vượt quá 22 sao cho:

a) 100 - x chia hết cho 4

b) 18 + 90 + x chia hết cho 9

Lời giải:

a) 100 - x chia hết cho 4. Mà 100 chia hết cho 4 nên x chia hết cho 4

Do đó x là bội của 4

Ta có: B(4) = {0; 4; 8; 12; 16; 20; 24;…} 

Vì x không vượt quá 22 nên x ∈ {0; 4; 8; 12; 16; 20}

Vậy x ∈ {0; 4; 8; 12; 16; 20}.

b) 18 + 90 + x chia hết cho 9. Mà 18 và 90 chia hết cho 9 nên x chia hết cho 9

Do đó x là bội của 9 

Ta có: B(9) = {0; 9; 18; 27;…}

Vì x không vượt quá 22 nên x ∈ {0; 9; 18}

Vậy x ∈ {0; 9; 18}.

Bài 2.28 trang 43 Toán lớp 6 Tập 1: Lớp 6B có 40 học sinh. Để thực hiện dự án học tập nhỏ, cô giáo muốn chia lớp thành các nhóm có số người như nhau, mỗi nhóm có nhiều hơn 3 người. Hỏi mỗi nhóm có thể có bao nhiêu người?

Lời giải:

Gọi số nhóm là x (nhóm, x ∈ N)

Vì cô giáo muốn chia lớp có 40 học sinh thành nhiều nhóm có số người như nhau nên 

40 ⁝ x hay X ∈ Ư(40)

Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}

Ta có bảng sau:

Vì mỗi nhóm có nhiều hơn 3 người nên mỗi nhóm có thể có 4 người; 5 người; 8 người; 10 người; 20 người hoặc 40 người.

Vậy mỗi nhóm có thể có 4 người; 5 người; 8 người; 10 người; 20 người hoặc 40 người.

Bài 2.29 trang 43 Toán lớp 6 Tập 1: Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là hai số nguyên tố sinh đôi. Em hãy liệt kê các cặp số nguyên tố sinh đôi nhỏ hơn 40.

Lời giải:

Các cặp số nguyên tố sinh đôi nhỏ hơn 40: 

+) 3 và 5

+) 5 và 7

+) 11 và 13

+) 17 và 19

+) 29 và 31.