Với Giải Toán lớp 6 trang 33 Tập 1 Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6. Mời các bạn đón xem:

Giải Toán lớp 6 trang 33 Tập 1 Kết nối tri thức

Luyện tập 3 trang 33 Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy cho biết:

a) 20 + 81 có chia hết cho 5 không. Vì sao?

b) 34 + 28 – 12 có chia hết cho 4 không. Vì sao?

Lời giải:

a) Vì 20 $⋮$ 5 và 81 5nên (20 + 81)5

Vậy 20 + 81 không chia hết cho 5.

b) Vì 28 $⋮$ 4, 12 $⋮$ 4và 344 nên (34 + 28 – 12)4.

Vậy 34 + 28 – 12 không chia hết cho 4.

Vận dụng 2 trang 33 Toán lớp 6 Tập 1: Tìm x thuộc tập {5; 25; 39; 54} sao cho tổng 20 + 45 + x không chia hết cho 5.

Lời giải:

Vì 20 ⁝ 5; 45 ⁝ 5, để (20 + 45 + x)  5 thì x  5.

Mà x thuộc tập {5; 25; 39; 54} do đó x = 39 hoặc x = 54

Vậy x ∈ {39;54}. 

Tranh luận trang 33 Toán lớp 6 Tập 1:

Lời giải:

Theo mình, hai số không chia hết cho 4 thì tổng của chúng có thể chia hết cho 4 hoặc không chia hết cho 4.

Ví dụ: 5 và 7 là hai số không chia hết cho 4 nhưng (5 + 7) = 12 ⁝ 4

           5 và 9 là hai số không chia hết cho 4 nhưng (5 + 9) = 14 4

Vậy hai số không chia hết cho 4 thì chưa kết luận được tổng có chia hết cho 4 hay không. 

Bài tập

Bài 2.1 trang 33 Toán lớp 6 Tập 1: Hãy tìm các ước của mỗi số sau: 30; 35; 17

Lời giải:

+) Lần lượt chia 30 cho các số tự nhiên từ 1 đến 30, ta thấy 30 chia hết cho 1; 2; 3; 5; 6; 10; 15; 30 nên Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.

+) Lần lượt chia 35 cho các số tự nhiên từ 1 đến 35, ta thấy 35 chia hết cho 1; 5; 7; 35 nên 

Ư(35) = {1; 5; 7; 35}. 

+) Lần lượt chia 17 cho các số tự nhiên từ 1 đến 17, ta thấy 17 chia hết cho 1; 17 nên 

Ư(17) = {1; 17}.

Bài 2.2 trang 33 Toán lớp 6 Tập 1: Trong các số sau, số nào là bội của 4? 16; 24; 35

Lời giải:

Vì 16 : 4 = 4, 24 : 4 = 6, 35 : 4 = 8 (dư 3)

Nên 16 $⋮$ 4; 24 $⋮$ 4; 344

Vậy các số là bội của 4 là: 16; 24.

Bài 2.3 trang 33 Toán lớp 6 Tập 1: Tìm các số tự nhiên x, y sao cho:

a) x ∈ B(7) và x < 70

b) y ∈ Ư(50) và y > 5

Lời giải:

a) Lần lượt nhân 7 với 0; 1; 2; 3; 4; 5; … ta được các bội của 7 là: 0; 7; 14; 21; 28; 35; 42; 49; 56; 63; 70;…

Ta được B(7) = {0; 7; 14; 21; 28; 35; 42; 49; 56; 63; 70;…}

Mà x ∈ B(7) và x < 70 nên x ∈ {0; 7; 14; 21; 28; 35; 42; 49; 56; 63}.

b) Lần lượt chia 50 cho các số từ 1 đến 50, ta thấy 50 chia hết cho 1; 2; 5; 10; 25; 50 nên 

Ư(50) = {1; 2; 5; 10; 25; 50}

Mà y ∈ Ư(50) và y > 5 nên y ∈ {10; 25; 50}.

Bài 2.4 trang 33 Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy cho biết tổng nào sau đây chia hết cho 5?

a) 15 + 1 975 + 2 019;

b) 20 + 90 + 2 025 + 2 050.

Lời giải:

a) Vì 15 $⋮$ 5; 1975 $⋮$ 5 nhưng 20195 nên (15 + 1 975 + 2 019)5

Vậy tổng 15 + 1 975 + 2 019 không chia hết cho 5.

b) Vì 20 $⋮$ 5; 90 $⋮$ 5; 2025 $⋮$ 5; 2050 $⋮$ 5 nên (20 + 90 + 2 025 + 2 050) $⋮$ 5

Vậy tổng 20 + 90 + 2 025 + 2 050 chia hết cho 5.

Bài 2.5 trang 33 Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy cho biết hiệu nào sau đây chia hết cho 8?

a) 100 - 40

b) 80 - 16

Lời giải:

a) Vì 1008 và 40 $⋮$ 8 nên (100 – 40)8

Vậy hiệu 100 – 40 không chia hết cho 8.

b) Vì 8 $⋮$ 8 và 16 $⋮$ 8 nên theo tính chất chia hết của một hiệu thì (80 - 16) $⋮$ 8

Vậy hiệu 80 – 16 chia hết cho 8. 

Bài 2.6 trang 33 Toán lớp 6 Tập 1: Khẳng định nào sau đây đúng?

a) 219.7 + 8 chia hết cho 7;

b) 8.12 + 9 chia hết cho 3.

Lời giải:

a) Vì 7 $⋮$ 7 nên (219.7) $⋮$ 7 và 87 do đó (219.7 + 8)7.

b) Vì 12 $⋮$ 3nên (8.12) $⋮$ 3 và 9 $⋮$ 3 do đó (8.12 + 9) $⋮$ 3.

Vậy khẳng định b là đúng.

Bài 2.7 trang 33 Toán lớp 6 Tập 1: Cô giáo muốn chia đều 40 học sinh để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở (bỏ trống trong trường hợp không chia được)

Lời giải:

Ta thấy số học sinh bằng số nhóm nhân với số người ở một nhóm (Số người, số nhóm đều là số tự nhiên khác 0)

Do đó: Số nhóm = Số học sinh : Số người ở một nhóm

            Số người ở một nhóm = Số học sinh : Số nhóm

Ta có bảng sau:

Với số nhóm là 6 thì số người ở một nhóm là: 40 : 6 vì  406 nên bỏ trống.

Bài 2.8 trang 33 Toán lớp 6 Tập 1: Đội thể thao của trường có 45 vận động viên. Huấn luyện viên muốn chia thành các nhóm để luyện tập sao cho mỗi nhóm có ít nhất 2 người và không quá 10 người. Biết rằng các nhóm có số người như nhau, em hãy giúp huấn luyện viên chia nhé.

Lời giải:

Gọi số người mỗi nhóm được chia là x (người)

Ta có mỗi nhóm có ít nhất 2 người và không quá 10 người nên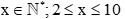 

Vì đội thể thao của trường có 45 vận động viên và huấn luyện viên chia thành các nhóm mà mỗi nhóm có số người như nhau nên 45 ⁝ x hay x ∈ Ư(45) 

Ta lại có Ư(45) = {1; 3; 5; 9; 15; 45}

Mà 2 ≤ x ≤ 10 do đó x ∈ {3; 5; 9}

Với số người mỗi nhóm được chia là 3 người thì số nhóm là: 45 : 3 = 15 (nhóm)

Với số người mỗi nhóm được chia là 5 người thì số nhóm là: 45 : 5 = 9 (nhóm)

Với số người mỗi nhóm được chia là 9 người thì số nhóm là: 45 : 9 = 5 (nhóm)

Vậy huấn luyện viên có thể chia thành 15 nhóm, 9 nhóm hoặc 5 nhóm

Bài 2.9 trang 33 Toán lớp 6 Tập 1: a) Tìm x thuộc tập {23; 24; 25; 26} biết 56 - x chia hết cho 8

b) Tìm x thuộc tập {22; 24; 45; 48} biết 60 + x không chia hết cho 6

Lời giải:

a) Vì 56 - x chia hết cho 8 mà 56 chia hết cho 8 nên theo tính chất chia hết của một hiệu thì x chia hết cho 8

Mà x thuộc tập {23; 24; 25; 26}, trong các số đó, chỉ có số 24 chia hết cho 8 nên x = 24

Vậy x ∈ 24 .

b) Vì 60 + x không chia hết cho 6 mà 60 chia hết cho 6 nên x không chia hết cho 6

Mà x thuộc tập {22; 24; 45; 48}, trong các số đó thì có hai số 22 và 45 không chia hết cho 6 nên x = 22 hoặc x = 45

Vậy x ∈ { 22;45 }.

Xem thêm các bài giải Toán lớp 6 Kết nối tri thức hay, chi tiết khác:

Giải Toán lớp 6 trang 30 Tập 1

Giải Toán lớp 6 trang 31 Tập 1

Giải Toán lớp 6 trang 32 Tập 1