Với giải sách bài tập Toán 6 Bài 8: Quan hệ chia hết và tính chất sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 8: Quan hệ chia hết và tính chất

Bài 2.1 trang 31 sách bài tập Toán lớp 6 Tập 1: Tìm kí hiệu thích hợp ( ⁝ ⋮̸ ) thay vào các dấu “?”

56  7;       63  8;       1 975  25;     2 020  20;           2 021  3

Lời giải:

+) Vì 56: 7 = 8 nên 56  7

+) Vì 63: 8 = 7 (dư 7) nên 63 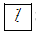 8

+) Vì 1 975: 25 = 79 nên 1 975  25

+) Vì 2 020: 20 = 101 nên 2 020  20

+) Vì 2 021: 3 = 673 (dư 2) nên 2 021 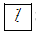 3

Bài 2.2 trang 31 sách bài tập Toán lớp 6 Tập 1: Hãy tìm tất cả các ước số của 56.

Lời giải:

Chia 56 cho lần lượt các số tự nhiên từ 1 đến 56 ta thấy 56 chia hết cho 1; 2; 4; 7; 8; 14; 28; 56.

Do đó các số 1; 2; 4; 7; 8; 14; 28; 56 là ước của 56

Vậy Ư(56) = {1; 2; 4; 7; 8; 14; 28; 56}.

Bài 2.3 trang 31 sách bài tập Toán lớp 6 Tập 1: Hãy tìm các bội số của 8 nhỏ hơn 100 và lớn hơn 50.

Lời giải:

Nhân 8 với lần lượt các số 0; 1; 2; 3; 4; … ta được: 0; 8; 16; 24; 32; 40; 48; 56; 64; 72; 80; 88; 96; 104; …

Do đó các số 0; 8; 16; 24; 32; 40; 48; 56; 64; 72; 80; 88; 96; 104; …là bội của 8

Bội số của 8 nhỏ hơn 100 và lớn hơn 50 là: 56; 64; 72; 80; 88; 96

Vậy bội số của 8 nhỏ hơn 100 và lớn hơn 50 là: 56; 64; 72; 80; 88; 96.

Bài 2.4 trang 31 sách bài tập Toán lớp 6 Tập 1: Khẳng định nào sau đây là đúng? Vì sao?

a) 2 021. 11 + 10 chia hết cho 11;

b) 97. 32 + 8 chia hết cho 8;

c) 2 020. 30 + 8. 5 chia hết cho 10.

Lời giải:

a) Vì 11 ⁝ 11 nên (2 021. 11) ⁝ 11

         10 ⁝ 11 

Suy ra (2 021. 11 + 10) ⁝ 11 (áp dụng tính chất chia hết của một tổng)

Do đó khẳng định a) là sai.

b) Vì 32 ⁝ 8 nên (97. 32) ⁝ 8

           8 ⁝ 8

Suy ra (97. 32 + 8) ⁝ 8

Do đó khẳng định b) là đúng.

c) Vì 30 ⁝ 10 nên (2 020. 30) ⁝ 10

          8. 5 = 40 ⁝ 10

Suy ra (2 020. 30 + 8. 5) ⁝ 10 (áp dụng tính chất chia hết của một tổng)

Do đó khẳng định c) là đúng.

Vậy các khẳng định đúng là b và c.

Bài 2.5 trang 31 sách bài tập Toán lớp 6 Tập 1: Không làm phép tính, hãy cho biết tổng nào sau đây chia hết cho 5.

a) 80 + 1 945 + 15;

b) 1 930 + 100 + 2 021.

Lời giải:

a) Vì 80 ⁝ 5; 1 945 ⁝ 5; 15 ⁝ 5 nên (80 + 1 945 + 15) ⁝ 5 (áp dụng tính chất chia hết của một tổng)

Vậy tổng 80 + 1 945 + 15 chia hết cho 5.

b) Vì 1 930 ⁝ 5; 100 ⁝ 5; 2 021 ⋮̸ 5 nên (1 930 + 100 + 2 021) ⋮̸ 5 (áp dụng tính chất chia hết của một tổng)

Vậy tổng 1 930 + 100 + 2 021 không chia hết cho 5.

Bài 2.6 trang 31 sách bài tập Toán lớp 6 Tập 1: Áp dụng tính chất chia hết của một tổng, hãy tìm x thuộc tập {15; 17; 50; 23} sao cho 

x + 20 chia hết cho 5.

Lời giải:

Để (x + 20) chia hết cho 5 mà 20 chia hết cho 5, áp dụng tính chất chia hết của một tổng

nên x phải chia hết cho 5

Các số chia hết cho 5 trong tập trên là: 15; 50

Vì x thuộc tập {15; 17; 50; 23} do đó x ∈ {15; 50}

Vậy x ∈ {15; 50}.

Bài 2.7 trang 31 sách bài tập Toán lớp 6 Tập 1: Áp dụng tính chất chia hết của một tổng, hãy tìm x thuộc tập {12; 19; 45; 70} sao cho 

x - 6 chia hết cho 3.

Lời giải:

Để (x - 6) chia hết cho 3 mà 6 chia hết cho 3, áp dụng tính chất chia hết của một tổng

nên x chia hết cho 3

Vì x thuộc tập {12; 19; 45; 70} do đó x ∈ {12; 45}

Vậy x ∈ {12; 45}.

Bài 2.8 trang 32 sách bài tập Toán lớp 6 Tập 1: Áp dụng tính chất chia hết của một tổng, hãy tìm x thuộc tập {20; 27; 50; 60} sao cho 

x + 32 không chia hết cho 4.

Lời giải:

Để (x + 32) không chia hết cho 4 mà 32 chia hết cho 4, áp dụng tính chất chia hết của một tổng nên x không chia hết cho 4

Vì x thuộc tập {20; 27; 50; 60} do đó x ∈ {27; 50}

Vậy x ∈ {27; 50}.

Bài 2.9 trang 32 sách bài tập Toán lớp 6 Tập 1:a) Tại sao tổng 2² + 2³ + 2⁴ + 2⁵ chia hết cho 3? 

b) Tại sao tổng 4²⁰ + 4²¹ + 4²² +4²³ chia hết cho 5?

Lời giải:

a) Ta có: 2² + 2³ + 2⁴ + 2⁵

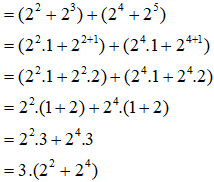
Vì 3 ⁝ 3 nên 3.(2² + 2⁴) 3 hay (2² + 2³ + 2⁴ + 2⁵) 3 

Vậy tổng 2² + 2³ + 2⁴ + 2⁵  chia hết cho 3

b) Ta có: 4²⁰ + 4²¹ + 4²² +4²³

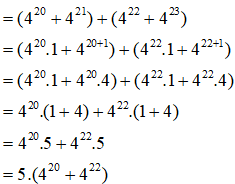
Vì 5 ⁝ 5 nên 5.(4²⁰ + 4²²) 5 hay (4²⁰ + 4²¹ + 4²² +4²³) 5 

Vậy tổng 4²⁰ + 4²¹ + 4²² +4²³  chia hết cho 5.

Bài 2.10 trang 32 sách bài tập Toán lớp 6 Tập 1: Khi chia số tự nhiên a cho 12, ta được số dư là 6. Hỏi a có chia hết cho 2 không? Có chia hết cho 4 không?

Lời giải:

Vì khi chia số tự nhiên a cho 12, ta được số dư là 6 nên a = 12. q + 6 (gọi q là thương của phép chia a cho 12)

+) Vì 12 ⋮ 2 nên (12. q) ⋮ 2

          6 ⋮ 2 

Do đó (12. q + 6) ⋮ 2 (áp dụng tính chất chia hết của một tổng) hay a ⋮ 2

Vậy a chia hết cho 2.

+) Vì 12 ⋮ 4 nên (12. q) ⋮ 4

    nhưng 6 ⋮̸ 4

Do đó (12. q + 6) ⋮̸ 4 (áp dụng tính chất chia hết của một tổng) hay a ⋮̸ 4

Vậy a không chia hết cho 4.

Bài 2.11 trang 32 sách bài tập Toán lớp 6 Tập 1: Để mở khóa két, Mai cần tìm được 8 chữ số ghép từ 4 số có hai chữ số, được cho trong bảng số dưới đây, các số đó được sắp xếp từ nhỏ đến lớn sao cho chúng chia hết cho 4 hoặc chia hết cho 5. Em hãy giúp Mai mở két nhé!

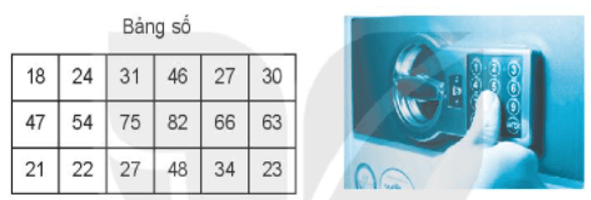
Lời giải:

+) Các số chia hết cho 4 trong bảng số trên là: 24; 48

+) Các số chia hết cho 5 trong bảng số trên là: 30; 75

Do đó 4 số có hai chữ số chia hết cho 4 hoặc chia hết cho 5 là: 24; 48; 30; 75.

Vì 24 < 30 < 48 < 75 nên cách sắp xếp từ nhỏ đến lớn là: 24; 30; 48; 75

Vậy để mở két Mai cần bấm lần lượt các chữ số 2; 4; 3; 0; 4; 8; 7; 5.

Lý thuyết Quan hệ chia hết và tính chất

1. Quan hệ chia hết

Cho hai số tự nhiên a và b (b ≠ 0). 

Nếu có số tự nhiên k sao cho a = kb thì ta nói a chia hết cho b kí hiệu là a   b.

Nếu a không chia hết cho b ta kí hiệu là a   b.

Ví dụ 1. Tìm kí hiệu thích hợp ( ; )   điền vào chỗ trống:

a) 12   2;                               b) 105   5;                                      c) 26   4.

Lời giải

a) Ta có 12 = 2.6 nên 12 chia hết cho 2 ta viết 12    2.

b) Ta có 105 = 5.21 nên 105 chia hết cho 5 ta viết 105   5.

c) Ta có 26 không chia hết cho 4 nên ta viết 26 4.

+ Ước và bội:

Nếu a chia hết cho b, ta nói b là ước của a và a là bội của b.

Ta kí hiệu Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.

Ví dụ 2. Khẳng định sau đây đúng hay sai?

a) 20 chia hết cho 5, 5 là ước của 20 và 20 là bội của 5.

b) 14 chia hết cho 3, 3 là ước của 14 và 14 là bội của 3.

c) 36 chia hết cho 9, 36 là ước của 9 và 9 là bội của 36.

Lời giải

a) Khẳng định a) đúng.

b) Vì 14 không chia hết cho 3 nên khẳng định b sai.

c) 36 chia hết cho 9 là đúng, trong đó 9 là ước của 36 và 36 là bội của 9 nên c sai.

+ Cách tìm ước và bội:

Muốn tìm các ước của a (a > 1), ta lần lượt chia a cho các số tự nhiên từ 1 đến a để xem a chia hết cho những số nào thì các số đó là ước của a.

Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt với 0; 1; 2; 3; …

Ví dụ 3. 

a) Hãy tìm tất cả các ước của 12.

b) Hãy tìm tất cả các bội của 8 nhỏ hơn 60.

Lời giải

a) Lần lượt chia 12 cho các số từ 1 đến 12, ta thấy 12 chia hết cho 1; 2; 3; 4; 6; 12 nên Ư(12) = {1; 2; 3; 4; 6; 12}.

b) Lần lượt nhân 8 với 0; 1; 2; 3; 4; 5; … ta được các bội của 8 là: 0; 8; 16; 24; 32; 40; 48; 56; 64; …

Các bội nhỏ hơn 60 của 8 là: 0; 8; 16; 24; 32; 40; 48; 56.

2. Tính chất chia hết của một tổng

+ Tính chất 1

Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

- Nếu a 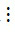  m và b  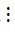 m thì (a + b)  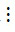 m.

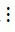- Nếu a   m, b 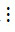  m và c  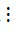 m thì (a + b + c)  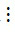 m.

Ví dụ 4. Không thực hiện phép tính, hãy cho biết:

a) 20 + 15 có chia hết cho 5 không. Vì sao?

b) 72 + 18 – 12 có chia hết cho 3 không. Vì sao?

Lời giải

a) Ta có 20 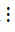 5 và 15  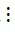 5 nên theo tính chất 1 thì tổng (20 + 1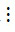5)   5.

b) Ta có 72 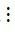 3, 18 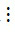 3 và 12  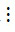3 nên theo tính chất 1 thì tổng (72 + 18 – 12) 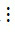 3.

+ Tính chất 2 

Nếu có một số hạng của một tổng không chia hết cho một số đã cho, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đã cho.

- Nếu a 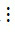 m và b  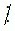m thì (a + b) 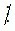m  .

- Nếu a 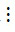 m, b m và c  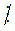m thì (a + b + c)  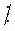 m.

Chú ý: Hai số không chia hết cho một số đã cho thì chưa chắc tổng của chúng không chia hết cho số đó.

Ví dụ 5. Các phát biểu sau đúng hay sai? 

a) 219.7 + 12 chia hết cho 7.

b) 2.3.4.11 + 22 + 45 không chia hết cho 11.

c) 8.12 + 9 chia hết cho 5.

Lời giải

a) Vì 219.7 là tích của 7 với số 219 nên chia hết cho 7 nhưng 12 không chia hết cho 7 nên 219.7 + 12   không chia hết cho 7. Do đó a sai.

b) Vì 2.3.4.11 là tích của 11 với các số 2; 3; 4 nên chia hết cho 11, 22 cũng chia hết cho 11 nhưng 45 không chia hết cho 11 nên 2.3.4.11 + 22 + 45 không chia hết cho 11. Do đó b đúng.

c) Ta có 8.12 không chia hết cho 5, 9 cũng không chia hết cho 5 nhưng tổng 8.12 + 9 = 105 lại chia hết cho 5. Do đó c đúng.