Cách tìm công thức truy hồi của dãy số hay, chọn lọc

Van Anh Ngày: 17-09-2024 Lớp 11

196

Tailieumoi.vn xin giới thiệu Cách tìm công thức truy hồi của dãy số hay, chọn lọc được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết công thức truy hồi của dãy số. Mời các bạn đón xem:

Cách tìm công thức truy hồi của dãy số

A. Công thức truy hồi

Dạng 1: Tìm số hạng tổng quát của dãy số (dạng đa thức) khi biết các số hạng đầu tiên

Dạng 2: Dạng cơ sở: Cho dãy (un) biết u1 = a và un+1 = q.un + d ∀ n ≥ 1 với q, d là các hằng số thực

Gồm 4 trường hợp, dạng này được gọi là dạng cơ sở vì:

+ Với 3 trường hợp 1, 2, và 3 dãy số trở thành các dãy đặc biệt đó là: dãy số hằng, cấp số cộng và cấp số nhân. Các dãy số này ta đều đã tìm được công thức của số
hạng tổng quát.

+ Trên cơ sở của 3 dãy này, để giải trường hợp 4: bằng phương pháp đặt một dãy số mới (vn) liên hệ với dãy số (un) bằng một biểu thức nào đó để có thể đưa được về dãy số (vn) mà (vn) dãy số hằng hoặc cấp cộng hoặc cấp số nhân.

+ Vấn đề đặt ra là: Mối liên hệ giữa (un) và (vn) bởi biểu thức nào mới có thể đưa dãy số (vn) thành dãy số hằng hoặc cấp số cộng hoặc cấp số nhân hoặc trường hợp 4.

B. Cách tìm công thức truy hồi

Dạng 1: Tìm số hạng tổng quát của dãy số (dạng đa thức) khi biết các số hạng đầu tiên

Ví du 1.1: Cho dãy số $\left(u_{n}\right)$ có dạng khai triển sau: 1 ;-1 ;-1 ; 1 ; 5 ; 11 ; 19 ; 29 ; 41 ; 55 ; ........

Hãy tìm công thức của số hạng tổng quát và tìm số tiếp theo?

Bài giải

Nhận xét: Với 10 số hạng đầu thế này, để tìm ra quy luật biểu diễn là rất khó. Với những cách cho này ta thường làm phương pháp sau:

Đặt:

$\begin{aligned} &\Delta u_{k}=u_{k+1}-u_{k} \\ &\Delta^{2} u_{k}=\Delta u_{k+1}-\Delta u_{k} \\ &\Delta^{3} u_{k}=\Delta^{2} u_{k+1}-\Delta^{2} u_{k} \end{aligned}$

Ta lập bảng các giá trị $\Delta u_{k}, \Delta^{2} u_{k}, \Delta^{3} u_{k} \ldots$ . . nếu đến hàng nào có giá trị không đổi thì dừng lại, sau đó kết luận $u_{n}$ là đa thức bậc 1,2,3, .............và ta đi tìm đa thức đó.

Dạng 2: Dạng cơ sở:

Cho dãy $\left(u_{n}\right) biết \left\{\begin{array}{l}u_{1}=a \\ u_{n+1}=q u_{n}+d, \quad n \geq 1\end{array}\right.$

Với q,d là các hằng số thực.

GIẢI:

- Trường hợp 1: Nếu $q=0 \Rightarrow\left\{\begin{array}{l}u_{1}=a \\ u_{n+1}=d, n \geq 1\end{array}\right. \Rightarrow u_{1}=a, u_{n}=d, \forall n \in \mathbb{N}^{*}, n \geq 2$

-Trường hợp 2: Nếu $q=1 \Rightarrow\left\{\begin{array}{l}u_{1}=a \\ u_{n+1}=u_{n}+d, n \geq 1\end{array}\right.$

$\Rightarrow\left(u_{n}\right)$ là cấp số cộng với số hạng đầu $u_{1}=a$ và công sai bằng d

$\Rightarrow u_{n}=a+(n-1) d$

-Trường hợp 3: Nếu $d=0 \Rightarrow\left\{\begin{array}{l}u_{1}=a \\ u_{n+1}=q u_{n}, n \geq 1\end{array}\right.$

$\Rightarrow\left(u_{n}\right)$ là cấp số nhân với số hạng đầu $u_{1}=a$ và công bội bằng q

$\Rightarrow u_{n}=a \cdot q^{n-1}$

-Trường hợp 4: Nếu $q \neq 0, q \neq 1, d \neq 0$ . Đặt dãy $\left(v_{n}\right) sao cho u_{n}=v_{n}+\frac{d}{1-q}(1)$

Thay ct(1) vào công thức truy hồi ta có:

$\begin{aligned} &v_{n+1}+\frac{d}{1-q}=q\left(v_{n}+\frac{d}{1-q}\right)+d \\ &\Rightarrow v_{n+1}=q v_{n}, n \geq 1 \end{aligned}$
$\Rightarrow\left(v_{n}\right)$ là một cấp số nhân với số hạng đầu $v_{1}=u_{1}-\frac{d}{1-q}=a-\frac{d}{1-q}$ và công bội bằng q

Ví du 2.1: Tìm công thức của số hạng tổng quát của các dãy $\left(u_{n}\right)$ biết:

$1) \left\{\begin{array}{l}u_{1}=-1 \\ u_{n+1}=u_{n}+3, n \geq 1\end{array}\right. 2) \left\{\begin{array}{l}u_{1}=1 \\ u_{n+1}=2 u_{n}+3, n \geq 1\end{array}\right. \left(\right. Ðs: \left.u_{n}=3 n-4\right)$

(Đs: $u_{n}=4.2^{n-1}-3$ )

Giải:

$1) \left\{\begin{array}{l}u_{1}=-1 \\ u_{n+1}=u_{n}+3, n \geq 1\end{array}\right.$

Vì $u_{n+1}=u_{n}+3, n \geq 1$

$\Rightarrow\left(u_{n}\right)$ là một cấp số cộng với số hạng đầu $u_{1}=-1$ và công sai d=3

$\Rightarrow u_{n}=u_{1}+(n-1) d=-1+3(n-1)=3 n-4$

$2) \left\{\begin{array}{l}u_{1}=1 \\ u_{n+1}=2 u_{n}+3, n \geq 1\end{array}\right.$

Nhận xét: Dãy số này có dạng 1 với q=1, d=3

Đặt dãy $\left(v_{n}\right)$ sao cho: $u_{n}=v_{n}+\frac{d}{1-q}=v_{n}-3 (1)$

Thay (1) vào công thức truy hồi ta được

$v_{n+1}-3=2\left(v_{n}-3\right)+3 \Rightarrow v_{n+1}=2 v_{n}$

$\Rightarrow\left(v_{n}\right)$ là cấp số nhân với số hạng đầu $v_{1}=u_{1}+3=1+3=4$ và công bội q=2

$\Rightarrow v_{n}=4.2^{n-1}=2^{n+1}$

$\Rightarrow u_{n}=v_{n}-3=2^{n+1}-3$

Nhân xét: Câu 1: $\left\{\begin{array}{l}u_{1}=-1 \\ u_{n+1}=u_{n}+3, n \geq 1\end{array}\right.$

Còn có các cách sau:

Cách 2:

Ta có:

$\begin{aligned} &u_{1}=-1 \\ &u_{2}=u_{1}+3 \\ &u_{3}=u_{2}+3 \end{aligned}$

$4. u_{n}=u_{n-1}+3$

Cộng vế với vế các hệ thức trên ta được:

$\begin{aligned} &u_{1}+u_{2}+u_{3}+\ldots \ldots+u_{n}=-1+u_{1}+u_{2}+u_{3}+\ldots . .+u_{n-1}+3(n-1) \\ &\Rightarrow u_{n}=-1+3(n-1) \\ &\Rightarrow u_{n}=3 n-4 \end{aligned}$

C. Bài tập

1. Bài tập trắc nghiệm

Bài 1: Cho dãy số có các số hạng đầu là: 4; 8; 12; 16; 20; 24;... Số hạng tổng quát của dãy số này là:

A. u_n = 4n B. u_n = 2n+ 2 C. u_n = 2n+ 5 D. u_n = 4n+ 2

Hướng dẫn giải:

Ta có:

4 = 4.1 8 = 4.2 12 = 4.3

16 = 4.4 20 = 4.5 24 = 4.6

Suy ra số hạng tổng quát u_n = 4n.

Chọn A .

Bài 2: Cho dãy số có các số hạng đầu là: .Số hạng tổng quát của dãy số này là:

A. u_n = 7n + 7. B. u_n = 7n .

C. u_n = 7n + 1. D. u_n : Không viết được dưới dạng công thức.

Hướng dẫn giải:

Ta có:

8 = 7 . 1 + 1 15 = 7 . 2 + 1 22 = 7 . 3 + 1

29 = 7 . 4 + 1 36 = 7 . 5 + 1

Suy ra số hạng tổng quát u_n = 7n + 1.

Chọn C.

Bài 3: Cho dãy số có các số hạng đầu là: 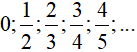Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) .Số hạng tổng quát của dãy số này là:

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Hướng dẫn giải:

Ta có:

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Suy ra số hạng tổng quát của dãy số là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Chọn B.

Bài 4: Cho dãy số có 4 số hạng đầu là: − 1, 3, 19, 53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.

A. u₁₀ = 971 B. u₁₀ = 837 C. u₁₀ = 121 D. u₁₀ = 760

Hướng dẫn giải:

Xét dãy (u_n) có dạng: u_n = an³ + bn² + cn + d

Theo giả thiết ta có: u₁ = − 1; u₂ = 3; u₃ = 19 và u₄ = 53

=> hệ phương trình:

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Giải hệ trên ta tìm được: a = 1;b = 0 ; c = −3 và d = 1.

Khi đó; số hạng tổng quát của dãy số là: u_n = n³ − 3n+ 1

Số hạng thứ 10: u₁₀ = 971 .

Chọn A .

Bài 5: Cho dãy số có các số hạng đầu là:0,1; 0,01; 0,001; 0,0001.... Số hạng tổng quát của dãy số này có dạng?

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Hướng dẫn giải:

Ta thấy:

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

=> Số hạng thứ n là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Chọn A.

Bài 6: Cho 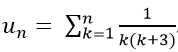Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Xác định công thức tính u_n

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Hướng dẫn giải:

Ta có:

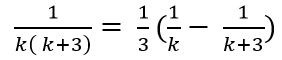
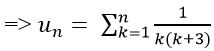
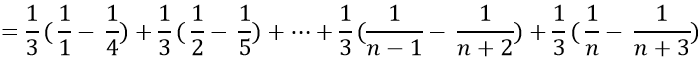
Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Chọn C.

Bài 7: Cho dãy số có các số hạng đầu là: − 2; 0; 2; 4; 6...Số hạng tổng quát của dãy số này có dạng?

A. u_n = −2n . B. u_n = − 2 + n . C. u_n = − 2(n+ 1) . D.u_n = − 2 + 2(n − 1)

Hướng dẫn giải:

Dãy số là dãy số cách đều có khoảng cách là 2 và số hạng đầu tiên là (−2) nên

u_n = − 2 + 2(n − 1) .

chọn D.

Bài 8: Cho dãy số có các số hạng đầu là: 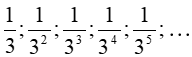Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) .Số hạng tổng quát của dãy số này là?

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Hướng dẫn giải:

Ta có; Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

=> Số hạng thứ n của dãy số là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Chọn C.

Bài 9: Cho dãy số (u_n) với 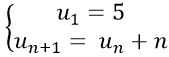Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) .Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Hướng dẫn giải:

Ta có:

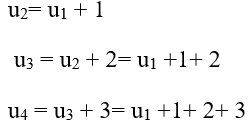
Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Chọn B.

Bài 10: Cho dãy số (u_n) với 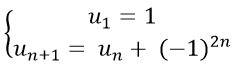Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. u_n = 1 + n B. u_n = n(n + 1) C. u_n = 1 + (−1)²ⁿ. D. u_n = n

Hướng dẫn giải:

* Ta có: u_n+1 = u_n + (−1)²ⁿ = u_n + 1 (vì (−1)²ⁿ = ((−1)²)ⁿ = 1

=> u₂ = 2 ; u₃ = 3; u₄ = 4; ...

Dễ dàng dự đoán được: u_n= n.

Thật vậy, ta chứng minh được : u_n = n bằng phương pháp quy nạp như sau:

+ Với n = 1 => u₁ = 1. Vậy (*) đúng với n = 1.

+ Giả sử (*) đúng với mọi n = k ( k ∈ N*), ta có u_k = k.

Ta đi chứng minh (*) cũng đúng với n = k + 1, tức là u_k+1 = k + 1

+ Thật vậy, từ hệ thức xác định dãy số (un ) ta có: u_k+1 = u_k + 1= k+ 1

Vậy (*) đúng với mọi n.

Chọn D.

Bài 11: Cho dãy số (u_n) với 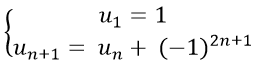Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Số hạng tổng quát un của dãy số là số hạng nào dưới đây?

A. u_n = 2 − n B. không xác định.

C. u_n = 1 − n. D. u_n = −n với mọi n.

Hướng dẫn giải:

+ Ta có: u₂ = 0; u₃ = −1; u₄ = −2...

Dễ dàng dự đoán được u_n = 2 − n.

+ Thật vậy; với n = 1 ta có: u₁ = 1 ( đúng)

Giả sử với mọi n = k ( k ∈ N*) thì u_k = 2 − k.

Ta chứng minh: u_k+1 = 2 − (k+ 1)

Theo giả thiết ta có: u_{k + 1} = u_k + (−1)^{2k + 1} = 2 − k − 1 = 2 − (k+1)

=> điều phải chứng minh.

Bài 12: Cho dãy số (u_n) với 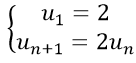Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) .Công thức số hạng tổng quát của dãy số này :

A. u_n = nⁿ⁻¹. B. u_n = 2ⁿ.

C. u_n = 2ⁿ⁺¹. D. u_n = 2^{n − 1}

Hướng dẫn giải:

+ Ta có:

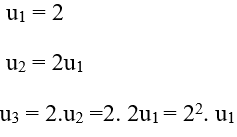
Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Hay u_n = 2ⁿ (vì u₁ = 2)

Chọn B.

Bài 13: Cho dãy số có các số hạng đầu là: −1; 1; −1; 1; −1; 1; ...Số hạng tổng quát của dãy số này có dạng

A.u_n = 1 B. u_n = − 1 C. u_n = (−1)n D. u_n = (−1)ⁿ⁺¹

Lời giải:

Đáp án: C

Ta có thể viết lại các số hạng của dãy như sau:

(−1)¹; (−1)²; (−1)³; (−1)⁴; (−1)⁵; (−1)⁶

=> Số hạng tổng quát của dãy số là u_n = (−1)ⁿ

Bài 14: Cho dãy số (u_n) với 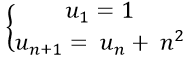Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

Lời giải:

Đáp án: C

Ta có:

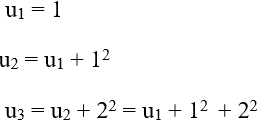
Áp dụng công thức: 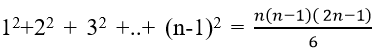Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) ( chứng minh bằng phương pháp quy nạp)

Bài 15: Cho dãy số (u_n) với 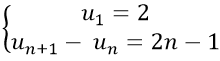Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. u_n = 2 + (n−1)². B. u_n = 2 + n². C.u_n = 2 + (n+1)². D. u_n = 2 − (n−1)².

Lời giải:

Đáp án: A

Ta có: u_n+1 − u_n = 2n − 1 suy ra: u_n+1 = u_n + 2n − 1

Theo đầu bài:

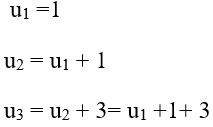
Áp dụng công thức: 1 + 3 + 5 + 7 +...+ (2n − 3) = (n−1)² (chứng minh bằng phương pháp quy nạp)

=>u_n = u₁ + (n−1)² = 2 + (n − 1)²

Bài 16: Cho dãy số (u_n) với 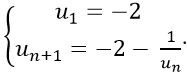Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Công thức số hạng tổng quát của dãy số này là:

Lời giải:

Đáp án: C

+ Ta có: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Dự đoán công thức số hạng tổng quát của dãy số là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

+ Chứng minh công thức trên bằng phương pháp quy nạp:

+ Ta có: 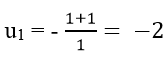Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) nên đúng với n= 1.

Giả sử đúng với n = k (k ∈ N*); tức là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Ta chứng minh đúng với n= k+ 1; tức là chứng minh: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Thật vậy ta có: 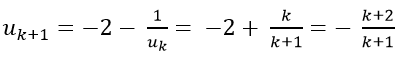Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) ( điều phải chứng minh)

Vậy Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Bài 17: Cho dãy số (u_n) với 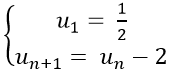Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Công thức số hạng tổng quát của dãy số này là:

Lời giải:

Đáp án: B

+ Ta có:

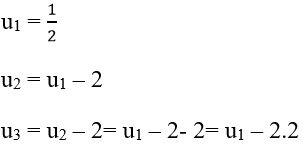
Hay Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Bài 18: Cho dãy số (u_n) với 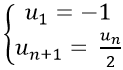Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Công thức số hạng tổng quát của dãy số này là:

Lời giải:

Đáp án: D

+ Ta có:

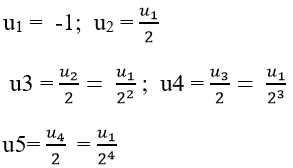
Bài 19: Cho 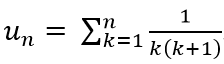Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Xác định công thức tính u_n

Lời giải:

Đáp án: A

+ Ta có:

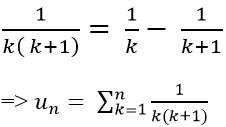
Bài 20: Cho dãy số (u_n) xác định bởi: 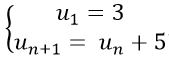Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Tìm công thức tính số hạng tổng quát của dãy số.

A. u_n = 3 + 5n B. u_n = 3 + 5.(n+1) C. u_n = 5.(n−1) D. u_n = 3 + 5.(n−1)

Lời giải:

Đáp án: D

Ta có:

u₂ = u₁ + 5 = 8

u₃ = u₂ + 5 = 13

u₄ = u₃ + 5 = 18

u₅ = u₄ + 5 = 23

Từ các số hạng đầu, ta dự đoán số hạng tổng quát un có dạng: u_n = 3 + 5.(n−1) (*) n ≥ 2

+ Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.

Với n = 2; u₂ = 3+ 5.(2−1) = 8(đúng). Vậy (*) đúng với n = 2

+Giả sử (*) đúng với n = k. Có nghĩa là : u_k = 3+ 5(k−1) (1)

Ta cần chứng minh (*) đúng với n = k+ 1. Có nghĩa là ta phải chứng minh:

u_k+1 = 3 + 5k

Thật vậy từ hệ thức xác định dãy số và theo (1) ta có:

u_k+1 = u_k + 5 = 3 + 5(k − 1) + 5 = 3 + 5k

Vậy (*) đúng khi n = k+ 1.

Kết luận (*) đúng với mọi số nguyên dương n.

Bài 21: Dãy số (u_n) được xác định bằng công thức: 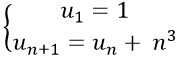Cách tìm công thức của số hạng tổng quát (cực hay có lời giải) . Tính số hạng thứ 100 của dãy số

A. 24502861 B. 24502501 C. 27202501 D. 24547501

Lời giải:

Đáp án: B

+ Trước tiên; ta đi tìm công thức tổng quát của dãy số.

+ Ta có: u_n+1 = u_n + n³ => u_n+1 − u_n = n³

Từ đó suy ra:

+ Cộng từng vế n đẳng thức trên:

+Bằng phương pháp quy nạp ta chứng minh được:

Vậy số hạng tổng quát là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

=> Số hạng thứ 100 của dãy số là: Cách tìm công thức của số hạng tổng quát (cực hay có lời giải)

Bài 22: Cho dãy số (u_n) xác định bởi u₁ = 2 và u_n+1 = 5u_n. Tính số hạng thứ 20 của dãy số?

A. 3. 5¹⁰ B. 2.5¹⁹ C. 2 . 5²⁰ D. 3 . 5²⁰

Lời giải:

Đáp án: B

Để tính số hạng thứ 20 của dãy số; ta đi tìm công thức xác định số hạng u_n

+ Ta có: u₂ = 10; u₃ = 50; u₄ = 250; u₅ = 1250; u₆ = 6250

+Ta dự đoán: u_n = 2. 5ⁿ⁻¹ (1) với mọi n ≥ 1. Ta chứng minh bằng phương pháp quy nạp

Với n = 1 ta có: u₁ = 2. 50 = 2 (đúng). Vậy (1) đúng với n = 1.

Giả sử (1) đúng với n = k (k ∈ N*). Có nghĩa là ta có: u_k = 2. 5^k−1

Ta phải chứng minh (1) đúng với n = k+ 1

Có nghĩa ta phải chứng minh: u_k+1 = 2.5^k

Từ hệ thức xác định dãy số (u_n) và giả thiết quy nạp ta có:

u_k+1 = 5u_k = 2. 5^k−1 . 5= 2 . 5^k (đpcm).

=> Số hạng thứ n của dãy số xác định bởi : u_n = 2. 5ⁿ⁻¹

=>Số hạng thứ 20 của dãy số là : u₂₀ = 2.5¹⁹.

Bài 22: Cho dãy số (u_n) xác định bởi u₁ = 3 và u_n+1 = √(1+ u_n²) với n ∈ N*. Tính số hạng thứ 28 của dãy số ?

A. 6 B. 7 C. 8 D. 9

Lời giải:

Đáp án: A

Để tính số hạng thứ 30 của dãy số ta đi tìm công thức xác định số hạng thứ n của dãy số>

+ Ta có:

Ta dự đoán : u_n = √(n+8) (1). Ta chứng minh bằng phương pháp quy nạp :

+ Với n = 1 có u₁ = √(1+8) = 3 (đúng). Vậy (1) đúng với n = 1 .

Giả sử (1) đúng với n = k ; k ∈ N* , có nghĩa ta có u_k = √(k+8) (2).

Ta cần chứng minh (1) đúng với n= k + 1. Có nghĩa là ta phải chứng minh:

u_{k + 1} = √(k+9)

Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:

Vậy (1) đúng với n = k + 1.

Kết luận số hạng tổng quát của dãy số là : u_n = √(n+8).

Số hạng thứ 28 của dãy số là : u₂₈= √(28+8) = 6.

2. Bài tập tự luyện

Bài 1. Xác định số hạng tổng quát của dãy số (u_n) được xác định bởi: u₁ = 3, u_n = 2u_n-1 với mọi n ≥ 2.

Bài 2. Cho dãy số (u_n) xác định bởi: $\{\begin{cases} u_{1} = 11 \\ u_{n + 1} = 10 u_{n} + 1 - 9 n, \forall n \in ℕ \end{cases}$ . Tìm công thức u_n theo n?

Bài 3. Cho dãy số (v_n) với $\{\begin{cases} v_{1} = - 2 \\ v_{n} = 3 v_{n - 1}, \forall n \geq 2 \end{cases}$ . Xác định số hạng tổng quát của dãy số?

Bài 4. Cho dãy số (u_n) có dạng khai triển sau: 1; -1; -1; 1; 5; 11; 19; 29; 41; 55; … Hãy tìm công thức của số hạng tổng quát và tìm số tiếp theo?

Bài 5. Xét dãy số (u_n) gồm tất cả các số nguyên dương chia hết cho 5: 5; 10; 15; 20; 25; 30; …

a) Viết công thức số hạng tổng quát u_n của dãy số.

b) Xác định số hạng đầu và viết công thức tính số hạng thứ n theo số hạng thứ n – 1 của dãy số. Công thức thu được gọi là hệ thức truy hồi.

Bài 6. Xét dãy số sau: 1, 4, 7, 10, 13,... Tìm số hạng tổng quát của dãy?

Bài 7. Viết công thức số hạng tổng quát u_n biết dãy số có các số hạng đầu là 5; 10; 15; 20; 25; 30; …

Bài 8. Cho dãy số có các số hạng đầu là: $1; \frac{1}{10}; \frac{1}{100}; \frac{1}{1000}; \frac{1}{10000}; ...$ . Tìm số hạng tổng quát của dãy số đã cho?