Tailieumoi.vn xin giới thiệu Đề cương ôn tập giữa kì 1 Toán 12 Kết nối tri thức năm 2024 – 2025. Tài liệu được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em làm quen với các dạng bài tập, nâng cao kỹ năng làm bài và rút kinh nghiệm cho bài thi giữa kì 1 Toán 12. Mời các bạn cùng đón xem:

Đề cương ôn tập giữa kì 1 Toán 12 Kết nối tri thức năm 2024

Đề cương ôn tập Toán 12 Giữa kì 1 Kết nối tri thức gồm hai phần: Nội dung ôn tập và Bài tập ôn luyện, trong đó:

- 5 bài tập trắc nghiệm;

- 5 bài tập tự luận;

I. NỘI DUNG ÔN TẬP

Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Bài 1. Tính đơn điệu và cực trị của hàm số

- Tính đơn điệu của hàm số: Khái niệm, sử dụng bảng biến thiên xét tính đơn điệu của hàm số.

- Cực trị của hàm số: Khái niệm, cách tìm cực trị.

Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

- Định nghĩa giá trị lớn nhất, giá trị nhỏ nhất.

- Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn.

Bài 3. Đường tiệm cận của đồ thị hàm số

- Đường tiệm cận ngang.

- Đường tiệm cận đứng.

- Đường tiệm cận xiên.

Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số

- Sơ đồ khảo sát hàm số.

- Khảo sát và vẽ đồ thị hàm số đa thức bậc ba.

- Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ.

Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

- Tốc độ thay đổi của một đại lượng.

- Một vài bài toán tối ưu hóa đơn giản.

II. BÀI TẬP ÔN LUYỆN

A. TRẮC NGHIỆM

Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Bài 1. Tính đơn điệu và cực trị của hàm số

Câu 1. Tìm khoảng đồng biến của hàm số: .

A. $(0;+\infty )$.                                              

B. $(-\infty ;0)$ .                   

C. $(-\infty ;-\sqrt{2})$và $(0;\sqrt{2})$.                       

D. $(\sqrt{2};+\infty )$ .

Câu 2. Tìm khoảng nghịch biến của hàm số: $y=\frac{3-2x}{x+7}$.

A. $(-\infty ;7)$ .                                              

B. $(-\infty ;+\infty )$.                

C. $(-\infty ;-7)$ và $(-7;+\infty )$.                        

D. $(-10;+\infty )$ .

Câu 3. Hàm số $y=\sqrt{2x-x^2}$ nghịch biến trên khoảng nào.

A.  (0 ;1).  

B. $\left(-\infty ;1\right)$.

C. (1; 2).                      

D. $\left(1;+\infty \right)$.

Câu 4. Cho các hàm số sau:

$\left(I\right):y=-x^3+3x^2-3x+1;\left(II\right):y=\sin x-2x;$$\left(III\right):y=-\sqrt{x^3+2};\left(IV\right):y=\frac{x-2}{1-x}$.

Hỏi hàm số nào nghịch biến trên toàn trục số?

A. (I), (II).

B. (I), (II) và (III).                 

C. (I), (II) và (IV).       

D. (II), (III).

Câu 5. Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Hỏi điểm cực tiểu của đồ thị hàm số y = f(x) là điểm nào?

A.  x = - 2

B. y = - 2 

C. M (0; - 2) 

D. N (2 ; 2)

Câu 6. Gọi M, n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số  $y=\frac{x^2+3x+3}{x+2}$. Khi đó giá trị của biểu thức $M^2-2n$ bằng:

A. 8.         

B. 7.          

C. 9.

D. 6.

Câu 7. Trong các câu sau câu nào đúng? Câu nào sai?

Cho hàm số $y=\frac{x+3}{x+2}$ .

A. Hàm số nghịch biến trên $ℝ\backslash \left\{-2\right\}$.

B. Hàm số nghịch biến trên $\left(-\infty ;-2\right)$  và $\left(-2;+\infty \right)$.

C. Hàm số đồng biến trên $ℝ$ .

D. Hàm số nghịch biến trên (- 4; - 3).

Câu 8. Cho hàm số $y=x^4-2x^2+1$ . Trong các mệnh đề sau mệnh đề nào đúng? Mệnh đề nào sai?

A. Hàm số có 3 điểm cực trị.

B. Hàm số đồng biến trên các khoảng $\left(-1;0\right)$ và $\left(1;+\infty \right)$.

C. Hàm số có 1 điểm cực trị.

D. Hàm số nghịch biến trên các khoảng $\left(-\infty ;-1\right)$ và (0; 1).

Câu 9. Cho hàm số $y=\sqrt{8+2x-x^2}$ . Xét tính đúng sai của các mệnh đề sau.

A. Tập xác định của hàm số là $D=\left[-2;4\right]$ .

B. Hàm số có $y^{\text{'}}=\frac{1-x}{\sqrt{8+2x-x^2}}$ .

C. Hàm số nghịch biến trên khoảng (1; 4).

D. Giá trị cực đại của hàm số là 0.

Câu 10. Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số $N\left(t\right)=-t^3+12t^2,0\le t\le 12$, trong đó N là số người bị nhiễm bệnh (đơn vị là trăm người) và t là thời gian (tuần). Gọi (a; b) là khoảng thời gian lâu nhất mà số người bị nhiễm bệnh tăng lên. Giá trị $P=2a^2-b^2=\mathrm{...............}$

Câu 11. Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức $N\left(t\right)=1000+\frac{100t}{100+t^2}$  (con), trong đó t là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để số lượng vi khuẩn đạt cực đại.

Điền đáp số: ………………

................................

................................

................................

B. TỰ LUẬN

Bài 1. Tìm các khoảng đơn điệu và các điểm cực trị của hàm số sau:

a) $y=-x^3+3x^2-4$ ;                               

b) $y=x^4+4x^3-1$.

Bài 2. Tìm các khoảng đơn điệu và cực trị của các hàm số sau

a) $y=\frac{2x+1}{x+1}$;                                          

b) $y=\frac{x^2+2x+2}{x+1}$ .

Bài 3. Tìm các khoảng đơn điệu và cực trị của các hàm số sau

a) $y=x^2+4\ln \left(3-x\right)$ ;                            

b) $y=\sqrt{x^2-2x}$ .

Bài 4. Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.

a) $f\left(x\right)=-x^3+3x^2+10$ trên đoạn $\left[-3;1\right]$ .

b) $f\left(x\right)=-2x^4+4x^2+3$  trên đoạn $\left[0;2\right]$ .

Bài 5. Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.

a) $f\left(x\right)=\frac{2x+3}{x+1}$  trên đoạn $\left[0;4\right]$ ;         

b) $f\left(x\right)=\frac{2x^2+4x+5}{x^2+1}$ trên R.

Bài 6. Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.

a) $y=e^{x^3-3x+3}$  trên đoạn $\left[0;2\right]$ ;               

b) $y=\frac{{\ln }^{2}x}{x}$  trên đoạn $\left[1;e^5\right]$.

Bài 7. Gọi A, B lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y=\frac{x+m^2+m}{x-1}$ trên đoạn $\left[2;3\right]$ . Tìm tất cả các giá trị thực của tham số m để $A+B=\frac{13}{2}$

III. Đề thi minh họa

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau: 

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (-∞;0).

B. (-∞;2).

C. (0;0).

D. (0;+∞).

Câu 2. Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình dưới đây.

Phát biểu nào sau đây là đúng?

A. x_CT = -1, x_CĐ = 1.

B. x_CT = -1, x_CĐ = 3.

C. x_CT = 3, x_CĐ = -1.

D. x_CT = 1, x_CĐ = -1.

Câu 3. Cho hàm số y = f(x) có đồ thị như hình dưới đây.

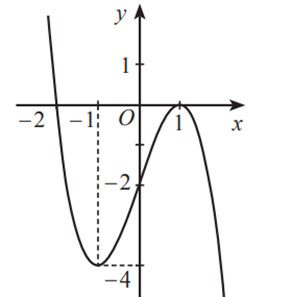
Giá trị nhỏ nhất của hàm số đã cho trên đoạn [-2;0] là:

A. -1.

B. -4.

C. -2.

D. 1.

Câu 4. Cho hàm số y = f(x) có đồ thị như hình dưới đây.

Phát biểu nào sau đây là đúng?

A. Đồ thị hàm số có đường tiệm cận đứng x = 2, đường tiệm cận ngang y = -1.

B. Đồ thị hàm số có đường tiệm cận đứng x = -1, đường tiệm cận ngang y = 2.

C. Đồ thị hàm số có đường tiệm cận đứng x = -1, đường tiệm cận ngang y = -1.

D. Đồ thị hàm số có đường tiệm cận đứng x = 2, đường tiệm cận ngang y = 0.

Câu 5. Cho hàm số y = f(x) có đồ thị như hình dưới đây.

Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng

A. y = x - 1.

B. y = -x - 1.

C. y = x + 1.

D. y = -x + 1.

Câu 6. Cho hàm số y = f(x) có đồ thị như hình dưới đây.

Tâm đối xứng của đồ thị hàm số có tọa độ là

A. (1;0).

B. (-1;1).

C. (2;-2).

D. (1;-1).

Câu 7. Phát biểu nào sau đây là đúng?

A. Với hai vectơ $\overrightarrow{a},\overrightarrow{b}$ bất kì và số thực k, ta có $k\left(\overrightarrow{a}-\overrightarrow{b}\right)=k\overrightarrow{a}-k\overrightarrow{b}$.

B. Với hai vectơ $\overrightarrow{a},\overrightarrow{b}$ bất kì và số thực k, ta có $k\left(\overrightarrow{a}-\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b}$.

C. Với hai vectơ $\overrightarrow{a},\overrightarrow{b}$ bất kì và số thực k, ta có $k\left(\overrightarrow{a}-\overrightarrow{b}\right)=k\left(\overrightarrow{a}+\overrightarrow{b}\right)$.

D. Với hai vectơ $\overrightarrow{a},\overrightarrow{b}$ bất kì và số thực k, ta có $k\left(\overrightarrow{a}-\overrightarrow{b}\right)=k\overrightarrow{a}-\overrightarrow{b}$.

Câu 8. Hàm số nào sau đây nghịch biến trên ℝ?

A. $y=\frac{x+1}{2-x}$.

B. y = -x³ - 3x - 2024.

C. y = -x³ - 2x² + x + 2024.

D. 2x² - 3x + 2024.

Câu 9. Giá trị lớn nhất của hàm số y = (x - 3)² . e^x trên đoạn [2;4] bằng

A. 0.

B. 4e.

C. e².

D. e⁴.

Câu 10. Quan sát bảng biến thiên và cho biết bảng biến thiên đó là của hàm số nào.

A. $y=\frac{-2x+1}{x+3}$.

B. $y=\frac{-2x+1}{x-3}$.

C. $y=\frac{2x-1}{x+3}$.

D. $y=\frac{2x-1}{x-3}$.

Câu 11. Cho hàm số $y=\frac{a{x}^2+bx+c}{x+d}$ có đồ thị như hình vẽ.

Trong các số a,b,c,d có bao nhiêu số có giá trị dương?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 12. Cho tứ diện đều ABCD có cạnh bằng a. Tích vô hướng $\overrightarrow{AB}\cdot \overrightarrow{AC}$ bằng 

A. a².

B. -a².

C. $\frac{1}{2}$a².

D. $\frac{\sqrt{3}}{2}$a².

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số y = f(x) xác định trên ℝ và có bảng biến thiên như sau:

a) Hàm số y = f(x) đồng biến trên mỗi khoảng (-∞;1) và (3;+∞).

b) Số điểm cực trị của hàm số đã cho là 3.

c) Hàm số y = f(x) có giá trị nhỏ nhất bằng 0.

d) Đồ thị hàm số không có đường tiệm cận.

Câu 2. Cho hàm số y = e^x - x + 3.

a) Hàm số đã cho nghịch biến trên ℝ.

b) Hàm số đã cho đạt cực đại tại x = 0.

c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ là (0;4).

d) Đồ thị hàm số đã cho không đi qua gốc tọa độ.

Câu 3. Cho hình hộp ABCD.A'B'C'D'.

a) Các vectơ bằng với vectơ $\overrightarrow{AD}$ là $\overrightarrow{BC},\overrightarrow{B^{\text{'}}{C}^{\text{'}}},\overrightarrow{A^{\text{'}}{D}^{\text{'}}}$.

b) Các vectơ đối của vectơ $\overrightarrow{DB}$ là $\overrightarrow{BD},\overrightarrow{D^{\text{'}}{B}^{\text{'}}}$.

c) $\overrightarrow{AB}+\overrightarrow{DC}=-2\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$.

d) $\overrightarrow{B{B}^{\text{'}}}-\overrightarrow{CA}=\overrightarrow{A{C}^{\text{'}}}$.

Câu 4. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = AC = AD = 1. Gọi M là trung điểm của BC.

a) $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$.

b) $\overrightarrow{AB}\cdot \overrightarrow{AD}=\overrightarrow{AC}\cdot \overrightarrow{AD}=\overrightarrow{AC}\cdot \overrightarrow{AB}=1$.

c) $\overrightarrow{AM}\cdot \overrightarrow{BD}=\frac{1}{2}$.

d) $\left(\overrightarrow{AM},\overrightarrow{BD}\right)=120°$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Giả sử hàm số $f\left(x\right)=x^3-6x^2+9x-5$ đạt cực đại tại x = a và đạt cực tiểu tại x = b. Giá trị của biểu thức M = 2a - 3b bằng bao nhiêu?

Câu 2. Cho hàm số y = e^x+2 + 5x - m với m là tham số thực. Với giá trị nào của m thì hàm số đã cho có giá trị lớn nhất trên đoạn [0;3] bằng e⁵?

Câu 3. Cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm của A'D' và C'D'. Gọi φ là góc giữa hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{A^{\text{'}}B}$. Số đo của góc φ bằng bao nhiêu độ?

Câu 4. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.

Câu 5. Cho hàm số $y=\frac{2x-1}{x-1}$ có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận của (C), M là một điểm bất kì trên (C) và tiếp tuyến của (C) tại M cắt hai tiệm cận tại A, B. Biết chu vi tam giác IAB có giá trị nhỏ nhất bằng $a+\sqrt{b}$ với a,b ∈ ℕ. Giá trị của biểu thức a - b + 4 bằng bao nhiêu?

Câu 6. Có ba lực cùng tác động vào một cái bàn như hình vẽ dưới. Trong đó hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ tạo với nhau một góc 110° và có độ lớn lần lượt là 9 N và 4 N, lực $\overrightarrow{F_3}$ vuông góc với mặt phẳng tạo bởi hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ và có độ lớn 7 N. Độ lớn hợp lực của ba lực trên là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị của Newton)?