20 Bài tập Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng lớp 8 (sách mới) có đáp án

Van Anh Ngày: 21-08-2024 Lớp 8

Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng. Mời các bạn đón xem:

Bài tập Toán 8 Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng

A. Bài tập Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng

Bài 1: Nếu tung một đồng xu 13 lần liên tiếp; có 9 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu??

A.
$\frac{9}{13}$
B.
$\frac{13}{35}$
C.
$\frac{4}{13}$
D.
$\frac{9}{22}$

Hướng dẫn giải:

Đáp án : A

Nếu tung một đồng xu 13 lần liên tiếp; có 9 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng: $\frac{9}{13}$

Bài 2: Tỉ lệ số học sinh đạt học sinh giỏi trong một lớp là $15 %$ . Gặp ngẫu nhiên một bạn trong lớp. Tính xác suất thực nghiệm của biến cố : “Học sinh đó đạt học sinh giỏi”

A.
0,15.
B.
0,85.
C.
0,5.
D.
0,25.

Hướng dẫn giải:

Đáp án : A

Xác suất của biến cố : “Học sinh đó đạt học sinh giỏi” là $\frac{15}{100} = 0, 15$

Bài 3: Bạn Hoàng Linh tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt $S$ còn bạn Tú Anh tung 100 lần và thấy có 55 lần xuất hiện mặt $S$ . Bạn Hoàng Linh nói xác suất thực nghiệm xuất hiện mặt $S$ là $\frac{30}{50}$ ; còn bạn Tú Anh bảo rằng xác suất thực nghiệm xuất hiện mặt $S$ là $\frac{55}{100}$ . Vậy trong hai bạn thì bạn nào nói đúng ?

A.
Bạn Tú Anh.
B.
Bạn Hoàng Linh.
C.
Cả hai bạn.
D.
Không bạn nào.

Hướng dẫn giải:

Đáp án : C

Bạn Hoàng Linh tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt $S$ nên xác suất thực nghiệm xuất hiện mặt $S$ là $\frac{30}{50}$ .

Bạn Tú Anh tung 100 lần và thấy có 55 lần xuất hiện mặt $S$ nên xác suất thực nghiệm xuất hiện mặt $S$ là $\frac{55}{100}$ .

Bài 4: Theo thống kê của một bệnh viện Sản, cứ 200 trẻ sơ sinh chào đời thì có 120 bé trai. Hãy ước lượng xem nếu có 1000 trẻ sơ sinh chào đời thì có bao nhiêu bé trai?

A.
400 bé.
B.
600 bé.
C.
800 bé.
D.
500 bé.
Hướng dẫn giải:

Đáp án : B

Xác suất thực nghiệm của biến cố A: “ Bé chào đời là bé trai” là $\frac{120}{200} = 0, 6 = 60 %$

Do đó ta có các ước lượng sau: $P (A) \approx 0, 6$

Gọi k là số bé trai trong 1000 bé. Thay giá trị ước lượng ở trên ta được:

$\frac{k}{1000} \approx 0, 6$ suy ra $k \approx 600$ . Vậy trong 1000 bé ước lượng có khoảng 600 bé trai.

Bài 5: Bạn An bỏ một số thẻ gỗ có đánh các số tự nhiên ( kích thước và khối lượng như nhau) vào trong một chiếc hộp. An lấy ra ngẫu nhiên một tấm thẻ, xem số rồi trả lại hộp. Lặp lại hành động đó 60 lần, An thấy có 24 lần lấy được thẻ ghi số chẵn. Biết trong hộp có 18 thẻ ghi số lẻ. Kết quả nào gần đúng với tổng số thẻ có trong hộp?

A.
30 thẻ.
B.
45 thẻ.
C.
12 thẻ.
D.
24 thẻ .
Hướng dẫn giải:

Đáp án : A

Gọi n là tổng số thẻ có trong hộp.

Xác suất lí thuyết của biến cố: “Lấy được thẻ ghi số lẻ” là $\frac{18}{n}$

An thấy có 24 lần lấy được thẻ ghi số chẵn nên An có 60-24=36 lần lấy được thẻ ghi số lẻ.

Xác suất thực nghiệm của biến cố: “Lấy được số thẻ ghi số lẻ trong 60 lần lấy thẻ” là $\frac{36}{60} = \frac{3}{5}$

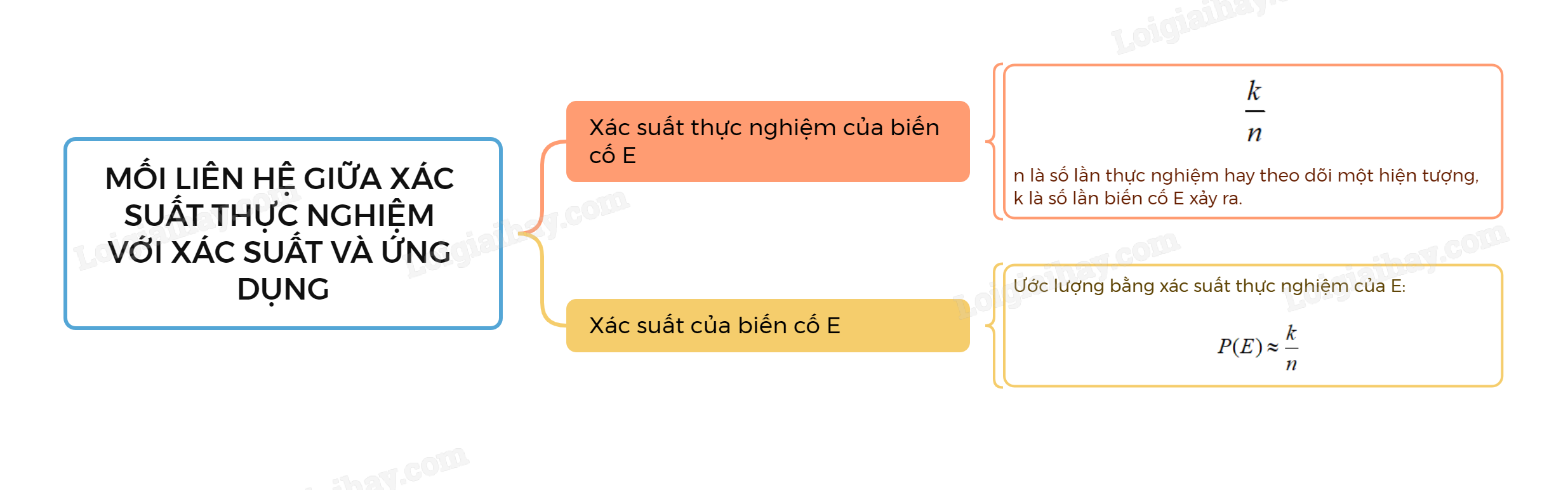
Do số phép thử lớn nên xác suất thực nghiệm gần bằng với xác suất lí thuyết nên ta có $\frac{18}{n} \approx \frac{3}{5}$ nên $n \approx 30$

B. Lý thuyết Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng

1. Xác suất thực nghiệm của một biến cố

Giả sử trong n lần thực nghiệm hoặc n lần theo dõi (quan sát) một hiện tượng ta thấy biến cố E xảy ra k lần. Khi đó xác suất thực nghiệm của biến cố E bằng $\frac{k}{n}$ , tức là bằng tỉ số giữa số lần xuất hiện của biến cố E và số lần thực hiện thực nghiệm hoặc theo dõi hiện tượng đó.

Ví dụ: Bạn Nam gieo một con xúc xắc 20 lần. Kết quả thu được như sau:

Số chấm	1	2	3	4	5	6
Số lần	2	4	5	3	2	4

Gọi A là biến cố “Nam gieo được số chấm lớn hơn 3”. Số chấm lớn hơn 3 là 4, 5 và 6 với số lần gieo được lần lượt là 3, 2 và 4. Khi đó số biến cố A xảy ra là: 3 + 2 + 4 = 9 (lần)

Vậy xác suất thực nghiệm của biến cố A là $\frac{9}{20}$ .

2. Mối liên hệ giữa xác suất thực nghiệm với xác suất

Xác suất của biến cố E được ước lượng bằng xác suất thực nghiệm của E:

$P (E) \approx \frac{k}{n};$

Trong đó n là số lần thực nghiệm hay theo dõi một hiện tượng, k là số lần biến cố E xảy ra.

Ví dụ: Trong 240 000 trẻ sơ sinh chào đời người ta có 123 120 bé trai.

Số bé gái chào đời là: 240 000 – 123 120 =116 880

Xác suất của biến cố “Trẻ sơ sinh là bé gái” là: $\frac{116880}{240000} = \frac{487}{1000} = 0, 487 = 48, 7 %$