Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Phép nhân và phép chia phân số được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Phép nhân và phép chia phân số. Mời các bạn đón xem:
Bài tập Toán 6 Phép nhân và phép chia phân số
A. Bài tập Phép nhân và phép chia phân số
Bài 1: Thực hiện phép tính
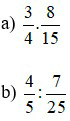
Lời giải:
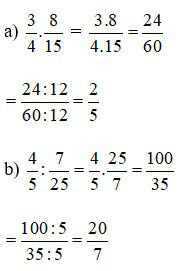
Bài 2: Thực hiện phép tính
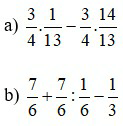
Lời giải:
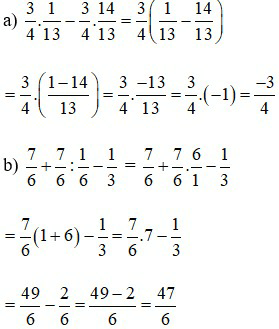
Bài 3: Tìm x
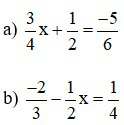
Lời giải:
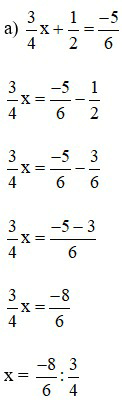
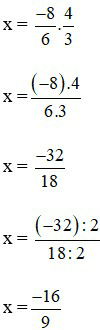
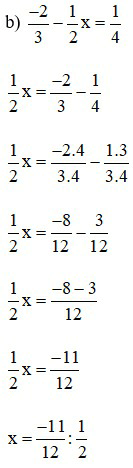
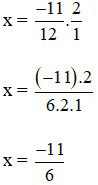
Bài 4: Một hình chữ nhật có chiều dài là 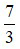 m và diện tích của hình chữ nhật là
m và diện tích của hình chữ nhật là 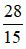 m2. Tính chiều rộng, chu vi hình chữ nhật đó.
m2. Tính chiều rộng, chu vi hình chữ nhật đó.
Lời giải:
Chiều rộng của hình chữ nhật là:
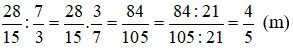
Chu vi hình chữ nhật là:
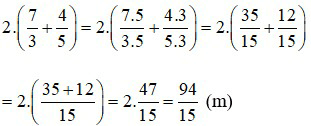
Vậy chiều rộng hình chữ nhật là 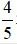 m và chu vi của nó là
m và chu vi của nó là 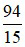 m.
m.
Bài 5. Tính giá trị biểu thức (tính hợp lí nếu có thể).
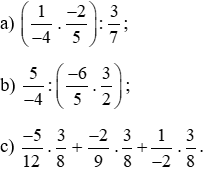
Lời giải:
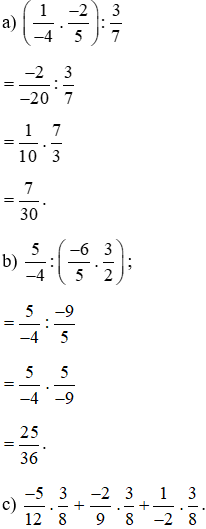

Bài 6. Tìm x, biết:
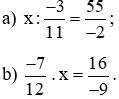
Lời giải:
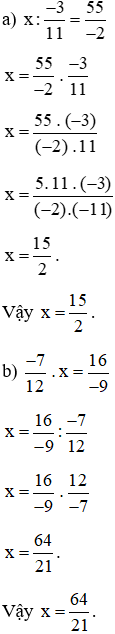
Bài 7. Một hình chữ nhật có chiều rộng là 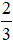 m, diện tích là
m, diện tích là 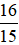 m2. Tính chiều dài của hình chữ nhật.
m2. Tính chiều dài của hình chữ nhật.
Lời giải:
Chiều dài của hình chữ nhật là:
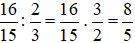 (m)
(m)
Vậy chiều dài của hình chữ nhật là 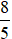 m.
m.
Bài 8. Tính giá trị biểu thức (tính hợp lí nếu có thể):
a) ;
b)
c)
d)
e)
Hướng dẫn giải
a)
;
b)
c)
;
d)
;
e)
.
Bài 9. Tìm x, biết:
a)
b) ;
c)
Hướng dẫn giải
a)
Vậy
b)
Vậy
c)
Vậy .
Bài 10. Sau một thời gian gửi tiết kiệm với số tiền là 8 triệu đồng, người gửi đi rút tiền và nhận số tiền lãi bằng số tiền gửi tiết kiệm. Hỏi sau khi rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?
Hướng dẫn giải
Vì số tiền lãi bằng số tiền gửi tiết kiệm nên số tiền lãi người đó nhận được là:
(đồng).
Tổng số tiền người đó nhận được là:
8 000 000 + 320 000 = 8 320 000 (đồng)
Vậy tổng số tiền người đó nhận được là 8 320 000 đồng.
Bài 11. Một khu đất hình chữ nhật có chiều dài m và diện tích là m2. Tính chiều rộng của khu đất đó.
Hướng dẫn giải
Chiều rộng của khu đất hình chữ nhật là:
(m).
Vậy chiều rộng của khu đất là m.
Câu 12. Tính giá trị của biểu thức
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: C
Câu 13. Điền số thích hợp vào ô trống:
Một ô tô chạy hết giờ trên một đoạn đường với vận tốc trung bình 40km/h.
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ giờ thì ô tô phải chạy với vận tốc trung bình là: ….. km/h
Trả lời:
Quãng đường ô tô đi được là:
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ giờ thì ô tô phải chạy với vận tốc trung bình là:
Câu 14. Chọn phát biểu đúng nhất trong các phát biểu sau:
A. Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
B. Phân số nào nhân với 1 cũng bằng chính nó.
C. Phân số nào nhân với 0 cũng bằng 0
D. Cả A, B, C đều đúng
Trả lời:
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số. Phân số nào nhân với 1 cũng bằng chính nó.
Phân số nào nhân với 00 cũng bằng 00
Vậy cả A, B, C đều đúng.
Đáp án cần chọn là: D
Câu 15. Tính:
A.
B. -2
C.
D.
Trả lời:
Đáp án cần chọn là: C
Câu 16. Kết quả của phép tính là:
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: D
Câu 17. Chọn câu sai:
A.
B.
C.
D.
Trả lời:
Đáp án A:
nên A đúng.
Đáp án B:
nên B đúng.
Đáp án C:
nên C đúng.
Đáp án D:
nên D sai.
Đáp án cần chọn là: D
Câu 18. Tìm số nguyên x biết
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: A
Câu 19. Tính
A.
B.
C.
D.
Trả lời:
Đáp án cần chọn là: C
Câu 20.
Điền số thích hợp vào ô trống
Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng ở độ cao của đáy vịnh Cam Ranh. Vậy độ cao của đáy sông Sài Gòn là.......mét
Trả lời:
Độ cao của đáy sông Sài Gòn là:
B. Lý thuyết Phép nhân và phép chia phân số
1. Phép nhân hai phân số
– Muốn nhân hai phân số, ta nhân các tử số với nhau và các mẫu số với nhau.
Cho a, b, c, d ∈ ℤ; b≠0; d≠0.
Khi đó phép nhân hai phân số ta có:
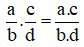
Ví dụ 1:
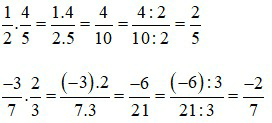
2. Tính chất của phép nhân
Cho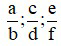 là các phân số với a, b, c, d, e, f ∈ ℤ; b≠0; d≠0; f≠0.
là các phân số với a, b, c, d, e, f ∈ ℤ; b≠0; d≠0; f≠0.
Khi đó ta có các tính chất của phép nhân như sau:
+ Tính giao hoán: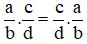
+ Tính kết hợp: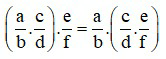
+ Tính nhân với 1: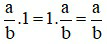
+ Tính phân phối giữa phép nhân với phép cộng: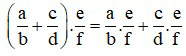
Ví dụ 2:
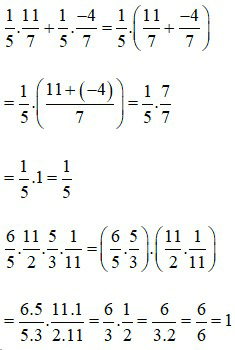
3. Phép chia phân số
a) Phân số nghịch đảo:
Phân số này được gọi là nghịch đảo của phân số kia nếu tích của chúng bằng 1
Cho a, b ∈ ℤ; a, b ≠ 0
Phân số 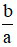 là phân số nghịch đảo của phân số
là phân số nghịch đảo của phân số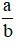 vì
vì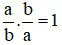
Ví dụ 3:
Phân số 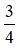 là phân số nghịch đảo của phân số
là phân số nghịch đảo của phân số 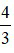 vì
vì 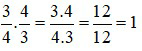
b) Phép chia phân số
– Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.
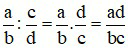 với a, b, c, d ∈ ℤ; b≠0; c≠0; d≠0
với a, b, c, d ∈ ℤ; b≠0; c≠0; d≠0
Ví dụ 4: