Bài 1: Thực hiện phép tính

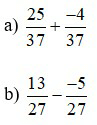
Lời giải:

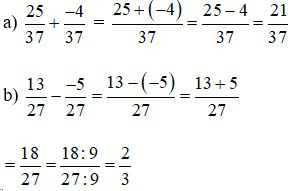
Bài 2: Thực hiện phép tính

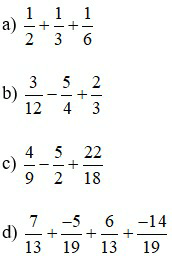
Lời giải:

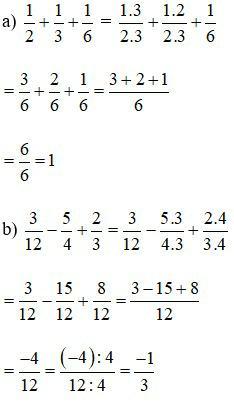
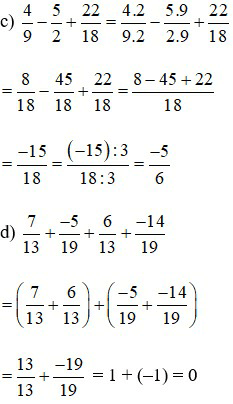
Bài 3: Tìm x

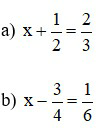
Lời giải:

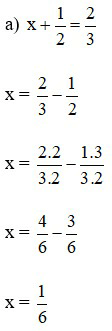
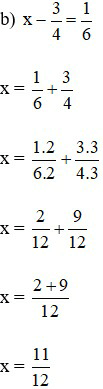
Bài 4. Tính giá trị biểu thức sau theo hai cách (có một cách dùng tính chất phép cộng phân số):

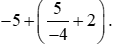
Lời giải:

Cách 1: Thực hiện đúng theo thứ tự phép tính (thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau).

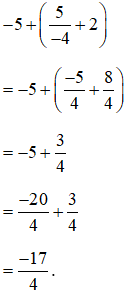
Cách 2: Dùng tính chất bỏ ngoặc. Sau đó sử dụng tính chất giao hoán và kết hợp của phép cộng.

Bài 5. Tìm số đối của:

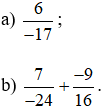
Lời giải:

a) Thêm dấu trừ trước phân số và rút gọn.

Số đối của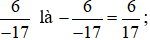 

b) Tính giá trị biểu thức rồi tìm số đối của kết quả tìm được hoặc đặt dấu trừ trước ngoặc chưa biểu thức.

Ta có: .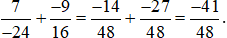

Số đối của 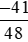 là phân số .

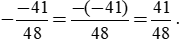Vậy số đối của .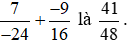

Bài 6. Người ta mở hai vòi nước cùng chảy vào một bể. Vòi thứ nhất mỗi giờ chảy được 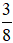 bể, vòi thứ hai mỗi giờ chảy được  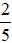bể. Nếu mở đồng thời cả hai vòi, mỗi giờ được mấy phần bể?

Lời giải:

Lượng nước hai vòi chảy được sau mỗi giờ bằng tổng lượng nước mỗi vòi chảy được mỗi giờ.

Nếu mở đồng thời cả hai vòi, mỗi giờ được:

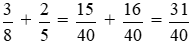 (phần bể).

Vậy nếu mở đồng thời cả hai vòi, mỗi giờ được 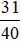 phần bể.

Bài 7. Tìm x biết:

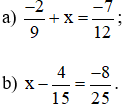
Lời giải:

Chuyển x sang một vế, bài toán đưa về tính tổng (hiệu) hai phân số.

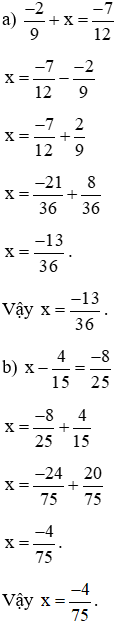
Bài 8. Tính:

a) $\frac{6}{13}+\frac{-15}{39}$

b) $\frac{-18}{24}+\frac{15}{21}$

c) $\frac{1}{6}-\frac{5}{6}$

d) $\frac{7}{21}-\frac{9}{-36}$

Hướng dẫn giải

a) $\frac{6}{13}+\frac{-15}{39}=\frac{6}{13}+\frac{\left(-15\right):3}{39:3}=\frac{6}{13}+\frac{-5}{13}=\frac{6+\left(-5\right)}{13}=\frac{1}{13}$

b) $\frac{-18}{24}+\frac{15}{21}=\frac{\left(-18\right):6}{24:6}+\frac{15:3}{21:3}=\frac{-3}{4}+\frac{5}{7}$

 $=\frac{\left(-3\right).7}{4.7}+\frac{5.4}{7.4}=\frac{-21}{28}+\frac{20}{28}=\frac{\left(-21\right)+20}{28}=\frac{-1}{28}$                  

c) $\frac{1}{6}-\frac{5}{6}=\frac{1-5}{6}=\frac{1+\left(-5\right)}{6}=\frac{-4}{6}=\frac{\left(-4\right):2}{6:2}=\frac{-2}{3}$

d) $\frac{7}{21}-\frac{9}{-36}=\frac{7:7}{21:7}-\frac{-9}{36}=\frac{1}{3}+\left(-\frac{-9}{36}\right)=\frac{1}{3}+\frac{9}{36}$

$=\frac{1}{3}+\frac{9:9}{36:9}=\frac{1}{3}+\frac{1}{4}=\frac{1.4}{3.4}+\frac{1.3}{4.3}$

$=\frac{4}{12}+\frac{3}{12}=\frac{4+3}{12}=\frac{7}{12}$

Bài 9. Tính một cách hợp lí:

a) $A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}$

b) $B=\frac{-3}{31}-\frac{6}{17}-\frac{-1}{25}+\frac{-28}{31}+\frac{-11}{17}-\frac{1}{5}$

c) $C=\frac{-5}{21}-\left(\frac{16}{21}-1\right)$

Hướng dẫn giải

a) $A=\frac{-5}{7}+\frac{3}{4}+\frac{-1}{5}+\frac{-2}{7}+\frac{1}{4}$

$=\frac{-5}{7}+\frac{-2}{7}+\frac{3}{4}+\frac{1}{4}+\frac{-1}{5}$

 $=\left(\frac{-5}{7}+\frac{-2}{7}\right)+\left(\frac{3}{4}+\frac{1}{4}\right)+\frac{-1}{5}$     

$=\frac{\left(-5\right)+\left(-2\right)}{7}+\frac{3+1}{4}+\frac{-1}{5}$

  $=\frac{-7}{7}+\frac{4}{4}+\frac{-1}{5}$

$=-1+1+\frac{-1}{5}$

$=0+\frac{-1}{5}$

$=\frac{-1}{5}$

Vậy $A=\frac{-1}{5}$.

b) $B=\frac{-3}{31}-\frac{6}{17}-\frac{-1}{25}+\frac{-28}{31}+\frac{-11}{17}-\frac{1}{5}$

$=\frac{-3}{31}+\frac{-28}{31}-\frac{6}{17}+\frac{-11}{17}-\frac{-1}{25}-\frac{1}{5}$

 $=\left(\frac{-3}{31}+\frac{-28}{31}\right)+\left(-\frac{6}{17}+\frac{-11}{17}\right)+\left(-\frac{-1}{25}-\frac{1}{5}\right)$  

$=\frac{\left(-3\right)+\left(-28\right)}{31}+\frac{\left(-6\right)+\left(-11\right)}{17}+\left(\frac{1}{25}-\frac{5}{25}\right)$

$=\frac{-31}{31}+\frac{-17}{17}+\frac{1-5}{25}$

$=\left(-1\right)+\left(-1\right)+\frac{-4}{25}$

$=-2+\frac{-4}{25}$

$=\frac{-50}{25}+\frac{-4}{25}$

$=\frac{-50+\left(-4\right)}{25}$

$=\frac{-54}{25}.$

Vậy $B=\frac{-54}{25}.$

c) $C=\frac{-5}{21}-\left(\frac{16}{21}-1\right)$

$=\frac{-5}{21}-\frac{16}{21}+1$

$=\left(\frac{-5}{21}-\frac{16}{21}\right)+1$

$=\frac{-5-16}{21}+1$

$=\frac{\left(-5\right)+\left(-16\right)}{21}+1$

$=\frac{-21}{21}+1$

= (‒1) + 1

= 0.

Vậy C = 0.

Bài 10. Tìm x, biết:

a) $x-\frac{1}{5}=\frac{2}{11}$

b) $x+\frac{7}{8}=\frac{13}{12}$

c) $-\frac{-7}{5}-x=\frac{4}{9}$

d) $x+\frac{5}{6}=\frac{16}{42}-\frac{-8}{56}$

Hướng dẫn giải

a) $x-\frac{1}{5}=\frac{2}{11}$

$x=\frac{2}{11}+\frac{1}{5}$

$x=\frac{2.5}{11.5}+\frac{1.11}{5.11}$

$x=\frac{10}{55}+\frac{11}{55}$

$x=\frac{10+11}{55}$

$x=\frac{21}{55}$

Vậy $x=\frac{21}{55}$

b) $x+\frac{7}{8}=\frac{13}{12}$      

 $x=\frac{13}{12}-\frac{7}{8}$ 

$x=\frac{13.2}{12.2}-\frac{7.3}{8.3}$

$x=\frac{26}{24}-\frac{21}{24}$

$x=\frac{26-21}{24}$

$x=\frac{5}{24}$ 

Vậy $x=\frac{5}{24}$

c) $-\frac{-7}{5}-x=\frac{4}{9}$

$\frac{7}{5}-x=\frac{4}{9}$

 $x=\frac{7}{5}-\frac{4}{9}$                                                              

$x=\frac{7.9}{5.9}-\frac{4.5}{9.5}$

$x=\frac{63}{45}-\frac{20}{45}$

$x=\frac{63-20}{45}$

$x=\frac{43}{45}$

Vậy $x=\frac{43}{45}$

d) $x+\frac{5}{6}=\frac{16}{42}-\frac{-8}{56}$

$x+\frac{5}{6}=\frac{16}{42}+\left(-\frac{-8}{56}\right)$

$x+\frac{5}{6}=\frac{16}{42}+\frac{8}{56}$

$x+\frac{5}{6}=\frac{16:2}{42:2}+\frac{8:8}{56:8}$

$x+\frac{5}{6}=\frac{8}{21}+\frac{1}{7}$

$x+\frac{5}{6}=\frac{8}{21}+\frac{1.3}{7.3}$

$x+\frac{5}{6}=\frac{8}{21}+\frac{3}{21}$

$x+\frac{5}{6}=\frac{8+3}{21}$

$x+\frac{5}{6}=\frac{11}{21}$

$x=\frac{11}{21}-\frac{5}{6}$

$x=\frac{11.6}{21.6}-\frac{5.21}{6.21}$

$x=\frac{66}{126}-\frac{105}{126}$

$x=\frac{66-105}{126}$

$x=\frac{-39}{126}$

$x=\frac{\left(-39\right):3}{126:3}$

$x=\frac{-13}{42}$

Vậy $x=\frac{-13}{42}$

Bài 11. Hai người cùng làm chung một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai phải mất 7 giờ mới xong công việc. Hỏi nếu làm chung thì mỗi giờ cả hai người làm được mấy phần công việc?

Hướng dẫn giải:

Coi toàn bộ công việc là  đơn vị.

Người thứ nhất làm xong công việc trong 4 giờ. Suy ra trong 1 giờ thì người thứ nhất làm được $\frac{1}{4}$ công việc.

Người thứ hai làm xong công việc trong 7 giờ. Suy ra trong  giờ người thứ hai làm được $\frac{1}{7}$ công việc.

Do đó trong 1 giờ, cả hai cùng làm thì được số phần công việc là:

$\frac{1}{4}+\frac{1}{7}=\frac{1.7}{4.7}+\frac{1.4}{7.4}=\frac{7}{28}+\frac{4}{28}=\frac{7+4}{28}=\frac{11}{28}$ (công việc).

Vậy nếu làm chung thì mỗi giờ cả hai người làm được $\frac{11}{28}$ công việc.

Bài 12. Chị An sau khi tốt nghiệp đại học và đi làm, chị nhận được tháng lương đầu tiên. Chị quyết định dùng $\frac{3}{5}$ số tiền để chi tiêu cùng gia đình và $\frac{1}{3}$ số tiền để mua quà tặng bố mẹ, số tiền còn lại chị để tiết kiệm. Số phần tiền để tiết kiệm của chị An là bao nhiêu?

Hướng dẫn giải

Coi toàn bộ số tiền lương thág đầu tiên của chị An là 1 đơn vị.

Số tiền còn lại sau khi chị dùng $\frac{3}{5}$ số tiền để chi tiêu cùng gia đình là:

$1-\frac{3}{5}=\frac{5}{5}-\frac{3}{5}=\frac{5-3}{5}=\frac{2}{5}$ (số tiền)

Số tiền để tiết kiệm của chị An là:

$\frac{2}{5}-\frac{1}{3}=\frac{2.3}{5.3}-\frac{1.5}{3.5}=\frac{6}{15}-\frac{5}{15}=\frac{6-5}{15}=\frac{1}{15}$ (số tiền)

Vậy số phần tiền  để tiết kiệm của chị An là $\frac{1}{15}$.

Câu 13. Tính $\frac{4}{15}-\frac{2}{65}-\frac{4}{39}$ ta được

A.$\frac{1}{39}$

B.$\frac{2}{15}$

C.$\frac{-2}{65}$

D.$\frac{1}{15}$

Trả lời:

$\frac{4}{15}-\frac{2}{65}-\frac{4}{39}=\frac{52}{195}-\frac{6}{195}-\frac{20}{195}=\frac{52-6-20}{195}=\frac{26}{195}=\frac{2}{15}$

Đáp án cần chọn là: B

Câu 14. Hai vòi nước cùng chảy vào một bể cạn. Vòi thứ nhất chảy riêng trong 10 giờ đầy bể, vòi thứ hai chảy riêng trong 8 giờ đầy bể. Vòi thứ ba tháo nước ra sau 5 giờ thì bể cạn. Nếu bể đang cạn, ta mở cả ba vòi thì sau 1 giờ chảy được bao nhiêu phần bể?

A.$\frac{17}{40}$

B.$\frac{1}{40}$

C.$\frac{1}{13}$

D. 1

Trả lời:

Trong 1 giờ, vòi thứ nhất chảy được là:  $1:10=\frac{1}{10}$(bể)

Trong 1 giờ, vòi thứ hai chảy được là:$1:8=\frac{1}{8}$  (bể)

Trong 1 giờ, vòi thứ ba tháo được là:$1:5=\frac{1}{5}$  (bể)

Sau 1 giờ, lượng nước trong bể có là:

$\frac{1}{10}+\frac{1}{8}-\frac{1}{5}=\frac{1}{40}$ (bể)

Đáp án cần chọn là: B

Câu 15. Phép tính $\frac{9}{7}-\frac{5}{12}$ là:

A.$\frac{73}{84}$

B.$\frac{-13}{84}$

C.$\frac{83}{84}$

D.$\frac{143}{84}$

Trả lời:

Ta có:$\frac{9}{7}-\frac{5}{12}=\frac{9}{7}+\left(\frac{-5}{12}\right)=\frac{108}{84}+\left(\frac{-35}{84}\right)=\frac{108+\left(-35\right)}{84}=\frac{73}{84}$

Đáp án cần chọn là: A

Câu 16. Tìm x biết $x=\frac{3}{13}+\frac{9}{20}$

A.$\frac{12}{33}$

B.$\frac{177}{260}$

C.$\frac{187}{260}$

D.$\frac{177}{26}$

Câu 17: Chọn câu đúng. Với a; b; m ∈ Z; m ≠ 0ta có

A.$\frac{a}{m}+\frac{b}{m}=\frac{a-b}{m}$

B.$\frac{a}{m}+\frac{b}{m}=\frac{a.b}{m}$

C.$\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$

D.$\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m+m}$

Trả lời:

Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.

$\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$

Đáp án cần chọn là: C

Câu 18: Phép cộng phân số có tính chất nào dưới đây?

A.Tính chất giao hoán 

B.Tính chất kết hợp 

C.Tính chất cộng với 0

D.Cả A, B, C đều đúng

Trả lời:

Phép cộng phân số có các tính chất:

+) Tính chất giao hoán: khi đổi chỗ các phân số trong một tổng thì tổng không đổi.

+) Tính chất kết hợp: Muốn cộng một tổng hai phân số với phân số thứ ba, ta có thể cộng phân số thứ nhất với tổng hai phân số còn lại.

+) Tính chất cộng với 0: tổng của một phân số với 0 bằng chính phân số đó.

Đáp án cần chọn là: D

Câu 19: Tổng $\frac{4}{6}+\frac{27}{81}$ có kết quả là

A.$\frac{1}{3}$

B.$\frac{4}{3}$

C.$\frac{3}{4}$

D. 1

Trả lời:

 $\frac{4}{6}+\frac{27}{81}=\frac{2}{3}+\frac{1}{3}=\frac{3}{3}=1$

Đáp án cần chọn là: D

Câu 20: Tính tổng hai phân số $\frac{35}{36}$ và$\frac{-125}{36}$

A.$\frac{-5}{2}$

B.$-\frac{29}{5}$

C.$\frac{-40}{9}$

D.$\frac{40}{9}$

Trả lời:

 $\frac{35}{36}+\frac{-125}{36}=\frac{35+\left(-125\right)}{36}=\frac{-90}{36}=\frac{-5}{2}$

Đáp án cần chọn là: A