Bài 1. So sánh hai phân số.

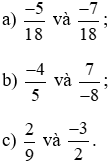
Lời giải:

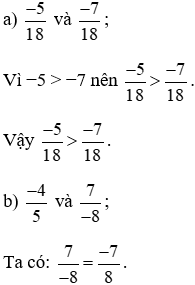
Quy đồng hai phân số 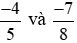 ta thực hiện: 

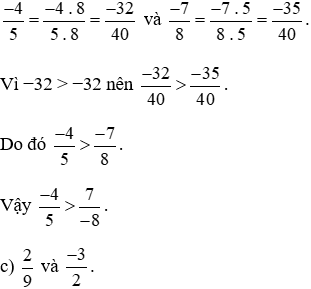
Ta có 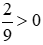 (vì phân số này là phân số dương).

Và 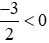 (vì phân số này là phân số âm).

Theo tính chất bắc cầu, phân số dương lớn hơn phân số âm nên .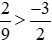

Vậy .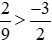

Bài 2. So sánh 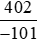 và −4.

Lời giải:

Cách 1: Đưa số nguyên và phân số về dạng phân số có cùng mẫu số dương, rồi so sánh tử số của hai phân số.

Ta có: 

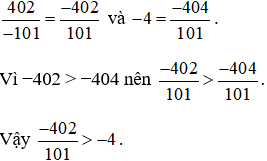
Cách 2: Đưa số nguyên về dạng phân số có mẫu số là 1, tử số là số nguyên đó, sau đó quy đồng mẫu số hai phân số đó (đưa hai phân số về cùng mẫu số dương).

Ta có: .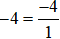

Quy đồng mẫu số hai phân số 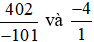, ta được:

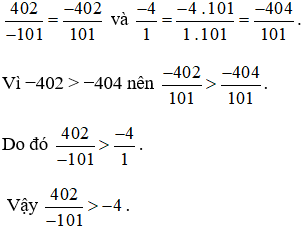
Bài 3. Sắp xếp các số theo thứ tự tăng dần: .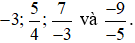

Lời giải:

Để sắp xếp các phân số theo thứ tự tăng dần, ta làm như sau:

Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.

- Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.

- Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.

Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).

Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần (phân số âm luôn bé hơn phân số dương).

Ta có .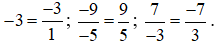

+ Các phân số dương: .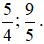

+ Các phân số âm: .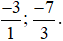

Ta so sánh các phân số dương với nhau, các phân số âm với nhau:

+ So sánh .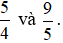

Mẫu số chung: 20.

Ta thực hiện: .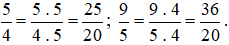

Vì 25 < 36 nên .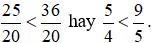

+ So sánh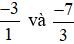 

Mẫu số chung: 3.

Ta thực hiện: 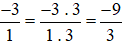 và giữ nguyên phân số .

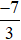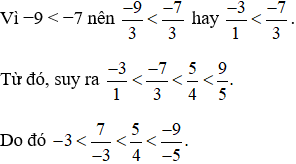
Vậy ta sắp xếp được theo thứ tự tăng dần như sau: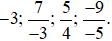 

Bài 4. Bình đọc hết một quyển sách trong 3 ngày. Ngày thứ nhất đọc được  quyển sách, ngày thứ hai đọc được 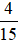 quyển sách, ngày thứ ba đọc được  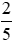quyển sách. Hỏi trong ba ngày đó thì ngày nào Bình đọc được nhiều nhất, ngày nào đọc được ít nhất?

Lời giải: 

Bài toán đưa về sắp xếp các phân số 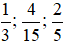 theo thứ tự tăng dần hoặc giảm dần. Sau đó kiểm tra xem ngày nào Bình đọc được nhiều nhất, ngày nào đọc được ít nhất.

Quy đồng mẫu số các phân số 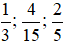 , ta được:

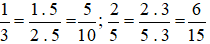 giữ nguyên phân số .

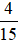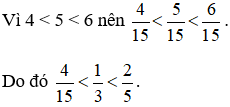
Vậy ngày thứ hai Bình đọc được nhiều nhất tương ứng với 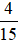 quyển sách, ngày thứ ba Bình đọc được ít nhất tương ứng với  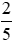quyển sách 

Bài 5: So sánh các phân số trong các trường hợp sau:

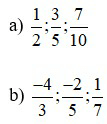
Lời giải:

a) Ta quy đồng mẫu số các phân số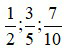 

BCNN (2; 5; 10) = 10

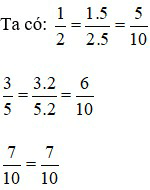
Vì 5 < 6 < 7 nên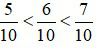 hay  .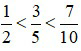

b) Ta quy đồng mẫu số các phân số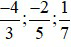 

BCNN (3; 5; 7) = 105

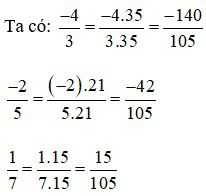
Vì 15 > –42 > –140 nên 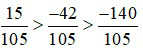hay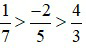

Bài 6. So sánh các phân số sau:

a) $\frac{2}{-5}$ và $\frac{-3}{5}$;

b) $\frac{1}{3}$ và $\frac{5}{6}$;

c) $\frac{5}{-7}$ và $\frac{-7}{11}$;

d) $\frac{5}{6}$ và  $\frac{63}{-70}$.

Hướng dấn giải

a) $\frac{2}{-5}$ và $\frac{-3}{5}$

Ta có: $\frac{2}{-5}=\frac{-2}{5}$

Do ‒2 > ‒3 nên $\frac{-2}{5}>\frac{-3}{5}$.

Vậy $\frac{2}{-5}>\frac{-3}{5}$;

b) $\frac{1}{3}$ và $\frac{5}{6}$

Ta có $\frac{1}{3}=\frac{1.2}{3.2}=\frac{2}{6}$

Vì 2 < 5 nên $\frac{2}{6}<\frac{5}{6}$ 

Vậy $\frac{1}{3}<\frac{5}{6}.$ 

c) $\frac{5}{-7}$ và $\frac{-7}{11}$ 

Ta có: $\frac{5}{-7}=\frac{-5}{7}=\frac{(-5).11}{7.11}=\frac{-55}{77}$ và $-\frac{7}{11}=\frac{-7}{11}=\frac{\left(-7\right).7}{11.7}=\frac{-49}{77}$ 

Vì 55 > 49 nên –55 < –49 do đó $\frac{-55}{77}<\frac{-49}{77}$.

Vậy $\frac{5}{-7}<\frac{-7}{11}.$ 

d) $\frac{5}{6}$ và $\frac{63}{-70}$ 

Ta có: $\frac{5}{6}>0$ và $\frac{63}{-70}<0$

Do đó $\frac{5}{6}>0>\frac{63}{-70}$

Vậy $\frac{5}{6}>\frac{63}{-70}$.

Bài 7. Sắp xếp các số sau theo thứ tự tăng dần: $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$

Hướng dấn giải

Ta chia các số $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$ thành hai nhóm:

Nhóm 1: gồm các số $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

Nhóm 2: gồm các số $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

Ta đi so sánh nhóm 1: $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

Có  $\frac{3}{4}=\frac{3.3}{4.3}=\frac{9}{12}$; $\frac{5}{6}=\frac{5.2}{6.2}=\frac{10}{12}$ và $1\frac{1}{2}=1+\frac{1}{2}=\frac{2}{2}+\frac{1}{2}=\frac{3}{2}=\frac{3.6}{2.6}=\frac{18}{12}.$ 

Do 9 < 10 < 18 nên $\frac{9}{12}<\frac{10}{12}<\frac{18}{12}$ 

Vậy $\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$ 

Ta đi so sánh nhóm 2: $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

Vì $\frac{2}{9}<\frac{5}{9}<\frac{5}{8}$ nên $-\frac{2}{9}>-\frac{5}{8}$

Vì $\frac{2}{9}>\frac{2}{12}>\frac{1}{12}$ nên $-\frac{2}{9}<-\frac{1}{12}$

Do đó $-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}$

Trong tất cả các phân số thì phân số âm luôn nhỏ hơn phân số dương, do đó ta có:

$-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}<\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$

Vậy ta có thể sắp xếp theo thứ tự tăng dần là $-\frac{5}{8};-\frac{2}{9};-\frac{1}{12};\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

Bài 8. Viết các đại lượng sau dưới dạng phân số và so sánh:

a) Thời gian nào dài hơn: 2 giờ 45 phút hay $2\frac{1}{4}$ giờ?      

b) Vận tốc nào nhỏ hơn: $\frac{5}{6}$ km/h hay $\frac{7}{9}$ km/h?

Hướng dẫn giải

a) Ta có 45 phút = $\frac{45}{60}$ giờ = $\frac{45:15}{60:15}$ giờ = $\frac{3}{4}$ giờ

Do đó 2 giờ 45 phút = $\left(2+\frac{3}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{3}{4}\right)$ giờ = $\frac{11}{4}$ giờ.

$2\frac{1}{4}$ giờ = $\left(2+\frac{1}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{1}{4}\right)$ giờ = $\frac{9}{4}$ giờ.

Vì 11 > 9 nên $\frac{11}{4}>\frac{9}{4}$

Do đó 2 giờ 45 phút > $2\frac{1}{4}$ giờ.

Vậy 2 giờ 45 phút dài hơn $2\frac{1}{4}$ giờ.

b) Ta có  $\frac{7}{9}=\frac{7.6}{9.6}=\frac{42}{54}$  và $\frac{5}{6}=\frac{5.9}{6.9}=\frac{45}{54}$

Vì 42 < 45 nên $\frac{42}{54}<\frac{45}{54}$        

Do đó $\frac{7}{9}$ km/h < $\frac{5}{6}$ km/h

Vậy vận tốc $\frac{7}{9}$ km/h nhỏ hơn $\frac{5}{6}$ km/h.

Bài 9. Điền số nguyên thích hợp vào các chỗ trống sau:

a) $\frac{10}{15}<\frac{\mathrm{...}}{15}<\frac{\mathrm{...}}{15}<\frac{\mathrm{...}}{15}<\frac{\mathrm{...}}{15}<\frac{15}{15}$;

b) $\frac{5}{-11}<\frac{\mathrm{...}}{-11}<\frac{\mathrm{...}}{-11}<\frac{\mathrm{...}}{-11}<\frac{1}{-11}$;

Hướng dẫn giải

a) Giả sử $\frac{10}{15}<\frac{a}{15}<\frac{b}{15}<\frac{c}{15}<\frac{d}{15}<\frac{15}{15}$

Ta thấy các phân số trên đều có mẫu số chung là 15, do đó ta có:

10 < a < b < c < d < 15

Mà a, b, c, d là các số nguyên nên a = 11, b = 12, c = 13, d = 14.

Vậy các số nguyên điền vào chỗ trống lần lượt là: 11; 12; 13; 14.

b) Giả sử $\frac{5}{-11}<\frac{x}{-11}<\frac{y}{-11}<\frac{z}{-11}<\frac{1}{-11}$

Suy ra  $\frac{-5}{11}<\frac{-x}{11}<\frac{-y}{11}<\frac{-z}{11}<\frac{-1}{11}$

Do đó ‒5 < ‒x < ‒y < ‒z < ‒1

Hay 5 > x > y > z > 1

Mà x, y, z là các số nguyên nên x = 4, y = 3, z = 2.

Vậy các số nguyên cần điền vào chỗ trống lần lượt là 4; 3; 2.

Câu 10: Chọn câu đúng:

A.  $\frac{11}{12}<\frac{-22}{12}$

B.  $\frac{8}{3}<\frac{-9}{3}$

C.  $\frac{7}{8}<\frac{9}{8}$

D.  $\frac{6}{5}<\frac{4}{5}$

Trả lời:

11 > (−22)  nên $\frac{11}{12}>\frac{-22}{12}$

8 > (−9) nên $\frac{8}{3}>\frac{-9}{3}$

7 < 9  nên $\frac{7}{8}<\frac{9}{8}$

6 > 4  nên $\frac{6}{5}>\frac{4}{5}$

Đáp án cần chọn là: C

Câu 11: Chọn số thích hợp điền vào chỗ trống sau: $\frac{7}{23}<\frac{\mathrm{...}}{23}$

A.9

B.7

C.5

D.4

Trả lời:

7 < 9 nên $\frac{7}{23}<\frac{9}{23}$

Đáp án cần chọn là: A

Câu 12: Không quy đồng mẫu số, em hãy so sánh $\frac{34}{111}$ và $\frac{198}{54}$ :

A.  $\frac{34}{111}<\frac{198}{54}$

B.  $\frac{34}{111}>\frac{198}{54}$

C.  $\frac{34}{111}\ge \frac{198}{54}$

D.  $\frac{34}{111}=\frac{198}{54}$

Trả lời:

Ta có:  $\frac{34}{111}<1$

Và  $\frac{198}{54}>1$

Do vậy:  $\frac{34}{111}<\frac{198}{54}$

Đáp án cần chọn là: A

Câu 13: Điền dấu thích hợp vào chỗ chấm $\frac{-12}{25}\mathrm{...}\frac{17}{-25}$

A. >  

B. <  

C. =  

D.Tất cả các đáp án trên đều sai

Trả lời:

 $\frac{17}{-25}=\frac{-17}{25}$

Vì -12 > -17 nên $\frac{-12}{25}>\frac{-17}{25}$ hay  $\frac{-12}{25}>\frac{17}{-25}$

Đáp án cần chọn là: A

Câu 14: Chọn câu sai

A.  $\frac{2}{-3}>\frac{-7}{8}$

B.  $\frac{-22}{33}=\frac{200}{-300}$

C.  $-\frac{2}{5}<\frac{196}{294}$

D.  $\frac{-3}{5}<\frac{39}{-65}$

Trả lời:

Đáp án A: Ta có:

$\frac{2}{-3}=\frac{-2}{3}=\frac{-2.8}{3.8}=\frac{-16}{24};\frac{-7}{8}=\frac{-7.3}{8.3}=\frac{-21}{24}$

Vì $\frac{-16}{24}>\frac{-21}{24}$ nên suy ra $\frac{2}{-3}>\frac{-7}{8}$ nên A đúng.

Đáp án B: Ta có:

 $\frac{-22}{33}=\frac{-22:11}{33:11}=\frac{-2}{3};\frac{200}{-300}=\frac{-200}{300}=\frac{-200:100}{300:100}=\frac{-2}{3}$

Vì $\frac{-2}{3}=\frac{-2}{3}$ nên suy ra $\frac{-22}{33}=\frac{200}{-300}$ nên B đúng.

Đáp án C: Ta có:

 $-\frac{2}{5}<0;\frac{196}{294}>0\Rightarrow \frac{-2}{5}<0<\frac{196}{294}\Rightarrow \frac{-2}{5}<\frac{196}{294}$nên C đúng.

Đáp án D: Ta có:

$\frac{39}{-65}=\frac{39:(-13)}{(-65):(-13)}=\frac{-3}{5}$

Vì $\frac{-3}{5}=\frac{-3}{5}$ nên suy ra $\frac{-3}{5}=\frac{39}{-65}$ nên D sai.

Đáp án cần chọn là: D

Câu 15. Sắp xếp các phân số $\frac{-3}{4};\frac{1}{12};\frac{-156}{149}$ theo thứ tự giảm dần ta được:

A.$\frac{-156}{149};\frac{-3}{4};\frac{1}{12}$

B. $\frac{1}{12};\frac{-156}{149};\frac{-3}{4}$

C. $\frac{-3}{4};\frac{-156}{149};\frac{1}{12}$

D. $\frac{1}{12};\frac{-3}{4};\frac{-156}{149}$

Câu 16. Cho $A=\frac{25.9-25.17}{-8.80-8.10}$ và $B=\frac{48.12-48.15}{-3.270-3.30}$. Chọn câu đúng

A. A < B

B. A = B

C. A > 1; B < 0

D. A > B

Câu 17. Số các cặp số nguyên (x; y) thỏa mãn $\frac{1}{18}<\frac{x}{12}<\frac{y}{9}<\frac{1}{4}$ là:

A. 2

B. 3

C. 1

D. 4

Câu 18. Có bao nhiêu phân số lớn hơn $\frac{1}{6}$ nhưng nhỏ hơn $\frac{1}{4}$ mà có tử số là 5.

A. 9

B. 10

C. 11

D. 12

Câu 19. So sánh các phân số $A=\frac{3535.232323}{353535.2323};B=\frac{3535}{3534};C=\frac{2323}{2322}$

A. A < B < C

B. A = B < C

C. A > B > C

D. A = B = C