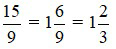Với giải sách bài tập Toán 6 Bài 24: So sánh phân số. Hỗn số dương sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương
Bài 6.11 trang 8 sách bài tập Toán lớp 6 Tập 2: Viết các phân số sau dưới dạng hỗn số
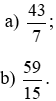
Lời giải:
Để chuyển phân số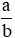 
về dạng hỗn số, ta cần xác định phần nguyên và phần phân số của số đó.
Lấy a chia b, ta được:
+ Phần số nguyên = Thương;
+ Phần phân số = số dư : số chia = số dư : b.
a) Ta có: 43 : 7 = 6 dư 1.
- Phần nguyên: 6;
- Phần phân số là: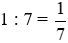 
.
Vậy phân số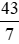 
viết dưới dạng hỗn số là 
.
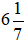b) Ta có: 59 : 15 = 3 dư 14.
- Phần nguyên: 3;
- Phần phân số là: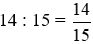 
.
Vậy phân số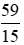 
viết dưới dạng hỗn số là 
.
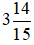Bài 6.12 trang 8 sách bài tập Toán lớp 6 Tập 2: Viết các hỗn số sau dưới dạng phân số.
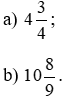
Lời giải:
Chuyển các hỗn số về phân số như sau:
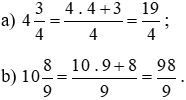
Vậy các hỗn số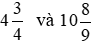 
được viết dưới dạng phân số lần lượt là: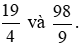 
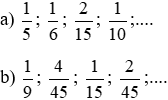
Lời giải:
a) Quy đồng các phân số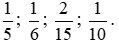 
Mẫu số chung = BCNN (5; 6; 15; 10) = 30.
Ta thực hiện:
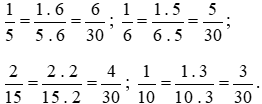
Nhận thấy: quy luật của dãy số này là các phân số có cùng mẫu số là 30; tử số giảm dần 1 đơn vị.
Do đó, phân số cần điền vào chỗ chấm là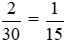 
b) Quy đồng các phân số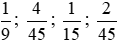 
Mẫu số chung = BCNN (9; 45; 15) = 45.
Ta thực hiện:
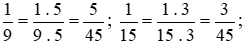
Giữ nguyên hai phân số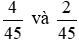 
Nhận thấy: quy luật của dãy số này là các phân số có cùng mẫu số là 45; tử số giảm dần 1 đơn vị.
Do đó, phân số cần điền vào chỗ chấm là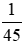 
Bài 6.14 trang 8 sách bài tập Toán lớp 6 Tập 2: Quy đồng mẫu số các phân số sau:
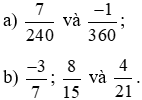
Lời giải:
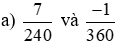
Mẫu số chung = BCNN (240; 360) = 720.
Ta quy đồng như sau:
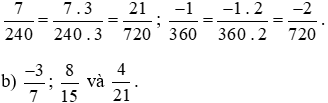
Mẫu số chung = BCNN (7; 15; 21) = 105.
Ta quy đồng như sau:
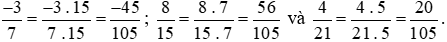
Bài 6.15 trang 9 sách bài tập Toán lớp 6 Tập 2: Rút gọn rồi quy đồng mẫu các phân số sau:
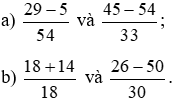
Lời giải:
a) * Rút gọn các phân số
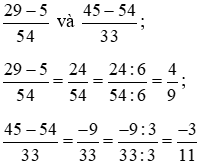
* Quy đồng các phân số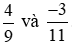 
Mẫu số chung là 99.
Ta thực hiện:
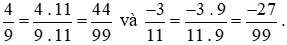
b) * Rút gọn các phân số
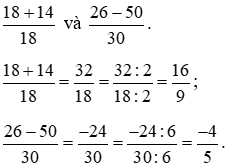
* Quy đồng các phân số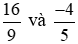 
Mẫu số chung là 45.
Ta thực hiện:
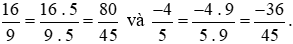
Bài 6.16 trang 9 sách bài tập Toán lớp 6 Tập 2: So sánh các phân số sau:
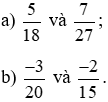
Lời giải:
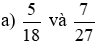
Mẫu số chung = BCNN (18; 27) = 54.
Ta quy đồng như sau:
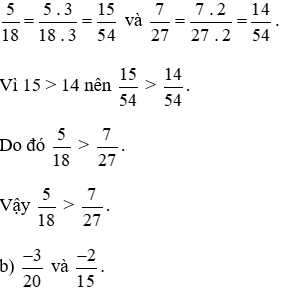
Mẫu số chung = BCNN (20; 15) = 60.
Ta quy đồng như sau:
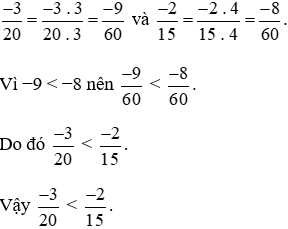
Lời giải:
Đối với bài toán này, ta tính vận tốc hai ngày của bạn Việt rồi so sánh.
Vận tốc ngày nào lớn hơn thì ngày đó bạn Việt đạp xe nhanh hơn.
Vận tốc đạp xe ngày thứ Bảy của bạn Việt là:
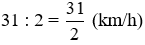
Vận tốc đạp xe ngày Chủ nhật của bạn Việt là:
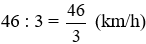
* Quy đồng hai phân số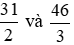 
Mẫu số chung là 6.
Ta thực hiện:
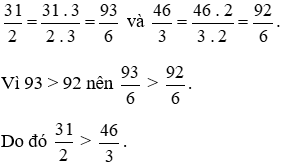
Vậy ngày thứ Bảy bạn Việt đạp xe nhanh hơn ngày Chủ nhật.
Bài 6.18 trang 9 sách bài tập Toán lớp 6 Tập 2: Sắp xếp các phân số sau theo thứ tự từ bé đến lớn.
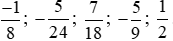
Lời giải:
Để sắp xếp các phân số theo thứ tự từ bé đến lớn, ta làm như sau:
Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.
+ Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.
+ Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.
Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).
Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần hoặc giảm dần (phân số âm luôn bé hơn phân số dương).
* Phân loại:
+ Nhóm phân số dương: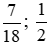 
+ Nhóm phân số âm: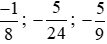 
.
* Ta so sánh các phân số dương với nhau, các phân số âm với nhau:
+ Nhóm phân số dương: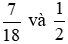 
Mẫu số chung: 18.
Ta thực hiện: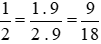 
và giữ nguyên phân số 
.
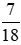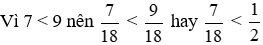
+ Nhóm phân số âm: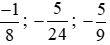 
.
Mẫu số chung: 72.
Ta thực hiện:
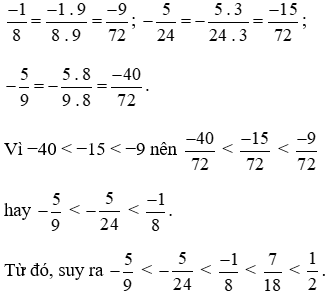
Vậy ta sắp xếp được theo thứ tự giảm dần như sau:
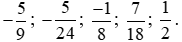
- Mua một gói giá 50 000 đồng.
- Mua hai gói giá 90 000 đồng.
- Mua ba gói giá 130 000 đồng.
Hôm nay Mai đi chợ cùng mẹ, mẹ bảo Mai mua ba gói là rẻ nhất. Em hãy giải thích tại sao mẹ Mai lại khuyên như thế nhé.
Lời giải:
Nếu mua hai gói thì giá tiền của mỗi gói là:
90 000 : 2 = 45 000 (đồng)
Nếu mua ba gói thì giá của mỗi gói là:
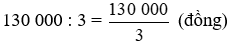
* Sắp xếp các số 50 000; 45 000;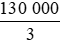 
theo thứ tự từ bé đến lớn như sau:
Mẫu số chung: 3.
Ta quy đồng như sau:
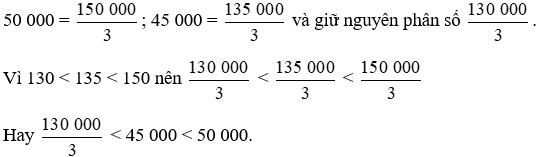
Do đó các số được sắp xếp theo thứ tự từ bé đến lớn là: 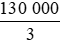; 45 000; 50 000.
Suy ra mua được 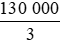đồng mỗi hộp là rẻ nhất.
Vậy mua ba gói xúc xích như trên là rẻ nhất.
Bài 6.20 trang 9 sách bài tập Toán lớp 6 Tập 2: Tìm số tự nhiên x sao cho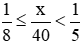 
Lời giải:
Quy đồng mẫu số các phân số: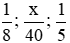 
Mẫu số chung: 40.
Ta thực hiện: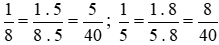 
và giữ nguyên phân số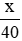 
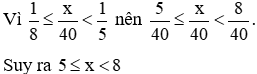
Do đó x = 5; 6; 7.
Vậy số tự nhiên x thỏa mãn 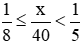thì x ∈ {5; 6; 7}.
Lý thuyết So sánh phân số. Hỗn số dương
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số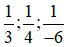 
ta làm như sau:
+ Đưa về các phân số có mẫu dương: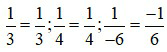 
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
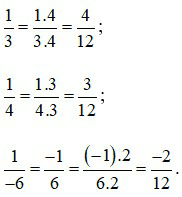
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: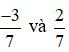 
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên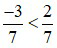 
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: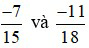 
.
BCNN (15; 18) = 90
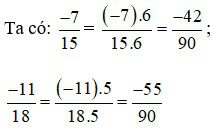
Vì –42 > –55 nên 
do đó,
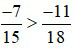
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi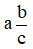 
là một hỗn số dương với a là phần nguyên và 
là phần phân số.
Ví dụ 4:
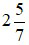là một hỗn số dương với phần nguyên là 2 và phần phân số là 
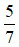. Khi đó ta đọc 
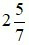là hai năm phần bảy.
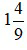là một hỗn số dương với phần nguyên là 1 và phần phân số là 
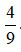. Khi đó ta đọc
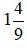là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số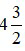 
sang phân số:
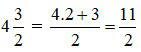
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số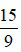 
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
