Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Chu vi và diện tích của một số tứ giác đã học được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chu vi và diện tích của một số tứ giác đã học. Mời các bạn đón xem:
Bài tập Toán 6 Chu vi và diện tích của một số tứ giác đã học
A. Bài tập Chu vi và diện tích của một số tứ giác đã học
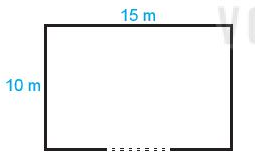
Bài 1. Một khu vườn hình chữ nhật có chiều dài 15m, chiều rộng 10m như hình dưới, cổng vào có độ rộng bằng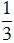 
chiều dài, phần còn lại là hàng rào. Hỏi hàng rào của khu vườn dài bao nhiêu mét?
Lời giải
Độ rộng của cửa là: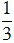 
.15 = 5(m) .
Chu vi hình chữ nhật là: 2.(10 + 15) = 2.25 = 50 (m)
Độ dài của hàng rào của khu vườn hình chữ nhật: 50 – 5 = 45 (m).
Bài 2. Một ngôi nhà có bãi có bảo quanh như hình bên.
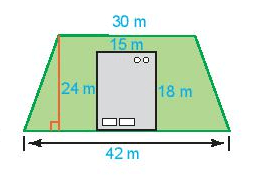
a) Hãy tính diện tích của bãi cỏ.
b) Nếu một túi hạt giống cỏ gieo vừa đủ trên 54m2 đất, thì cần bao nhiêu túi hạt giống để gieo vừa hết bãi cỏ?
Lời giải
Diện tích cả bãi cỏ và khu đất làm nhà là:
(30 + 42).24:2 = 864 (m2).
Diện tích khu đất làm nhà là:
15.18 = 270 (m2).
a) Diện tích cả bãi cỏ là:
864 – 270 = 594 (m2).
Vậy diện tích bãi cỏ là 594 m2.
b) Để gieo hết bãi cỏ thì cần số túi hạt giống là: 594:54 = 11 (túi).
Vậy cần tất cả 11 túi hạt giống để gieo hết bãi cỏ.
Bài 3. Cho hình thang MNPQ có diện tích là 60 cm2, MQ = 6 cm, NP = 9 cm. Kẻ đường cao MH và tính độ dài của đường cao đó.
Hướng dẫn giải
Kẻ đường cao MH của hình thang MNPQ (như hình vẽ).
Diện tích hình thang là:
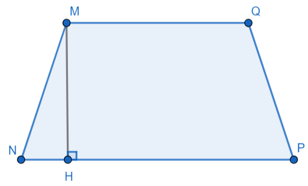
Vậy độ dài đường cao MH bằng 8 cm.
Bài 4. Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Loại gạch lát nền được sử dụng là gạch hình chữ nhật có chiều dài 20 cm, chiều rộng 50 cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể)?
Hướng dẫn giải
Diện tích căn phòng hình chữ nhật là:
8 . 6 = 48 (m2)
Diện tích của một viên gạch hình chữ nhật là:
20 . 50 = 1 000 (cm2) = 0,1 (m2).
Số viên gạch bác Khôi cần dùng là:
48 : 0,1 = 480 (viên).
Vậy để lát nền căn phòng hình chữ nhật, bác Khôi phải sử dụng 480 viên gạch.
Bài 5. Người ta cần xây tường rào và lát cỏ cho một khu vui chơi như hình dưới đây. Chi phí xây tường rào mỗi mét tường tốn 150 000 đồng, còn chi phí lát cỏ mỗi mét vuông tốn 100 000 đồng. Tính tổng số tiền cần để xây tường rào và lát cỏ cho một khu vui chơi.
Hướng dẫn giải
Ta lấy các điểm A, B, C, D, E, F, G, H (như hình vẽ).
Độ dài cạnh AH là:
AH = BC + DE + FG = 4 + 4 + 4 = 12 (cm).
Vì người ta xây tường rào xung quanh khu vườn, nên số mét tường rào chính là chu vi của khu vườn.
Chu vi khu vui chơi là:
AB + BC + DE + EF + FG + GH + AH
= 12 + 4 + 4 + 4 + 4 + 4 + 4 + 12 + 12
= 12 . 3 + 4 . 6 = 36 + 24 = 60 (m).
Số tiền để xây tường rào cho khu vui chơi là:
150 000 . 60 = 9 000 000 (đồng).
Diện tích khu vui chơi bằng tổng của hình vuông ABGH có cạnh bằng 12 cm và hình vuông CDEF có cạnh bằng 4 m.
Diện tích hình vuông ABGH là:
122 = 144 (m2).
Diện tích hình vuông CDEF là:
42 = 16 (m2).
Diện tích khu vui chơi là:
144 + 16 = 160 (m2).
Số tiền để lát cỏ cho khu vui chơi là:
100 000 . 160 = 16 000 000 (đồng).
Tổng số tiền cần để xây tường rào và lát cỏ cho một khu vui chơi là:
9 000 000 + 16 000 000 = 25 000 000 (đồng).
Vậy tổng số tiền cần để xây tường rào và lát cỏ cho một khu vui chơi là 25 000 000 đồng.
Câu 6. Một mảnh giấy hình chữ nhật có chiều dài 12cm và diện tích mảnh giấy hình chữ nhật là 96 cm2. Tính chu vi mảnh vườn hình chữ nhật:
A. 8 cm
B. 30 cm
C. 40 cm
D. 60 cm
Lời giải
Chiều rộng của mảnh vườn hình chữ nhật là: 96:12 = 8 cm.
Chu vi của mảnh vườn hình chữ nhật là: 2.(8 + 12) = 40 cm.
Đáp án: C
Câu 7. Một hình thang cân có diện tích 200 m2 và chiều cao là 10m. Tính tổng độ dài hai đáy của hình thang cân:
A. 40 m
B. 20 m
C. 10 m
D. 2 m
Lời giải
Trung bình cộng hai đáy là: 200:10 = 20 m.
Vậy tổng độ dài hai đáy là: 20.2 = 40m.
Đáp án: A
Câu 8. Bác An muốn làm hàng rào cho khu vườn hình vuông trồng hoa hồng của mình. Biết khu vườn có cạnh 5m, tính độ dài hàng rào?
A. 25m
B. 20m
C. 10m
D. 5m
Lời giải
Độ dài hàng rào chính là chu vi khu vườn.
Chu vi khu vườn là: 4.5 = 20m.
Vậy độ dài khu vườn của bác An là: 20m.
Đáp án: B
Câu 9. Cho hình thang cân có tổng hai đáy bằng 18 dm và chu vi hình thang cân 340 cm. Độ dài cạnh bên của hình thang cân là:
A. 16dm
B. 8 dm
C. 16cm
D. 8cm
Lời giải
Đổi 340 cm = 34 dm.
Tổng độ dài hai cạnh bên là: 34 – 18 = 16 dm.
Vạy độ dài cạnh bên của hình thang cân là: 16:2 = 8 dm.
Đáp án: B
Câu 10. Hình vuông có diện tích 64 m2. Độ dài cạnh hình vuông là:
A. 16 m
B. 36 cm
C. 8 m
D. 8 cm
Lời giải
Gọi cạnh hình vuông là a (m) (a > 0)
Khi đó diện tích của hình vuông là: a2 = 64(m2).
Suy ra a = 8 m.
Đáp án: C
Câu 11. Diện tích hình bình hành có chiều dài một cạnh 20 cm và chiều cao tương ứng 5 cm là:
A. 50 cm2
B. 100 cm2
C. 10 cm2
D. 5 cm2
Lời giải
Diện tích hình bình hành là: 20.5 = 100 (cm2).
Vậy diện tích hình bình hành là 100 cm2
Đáp án: B
Câu 12. Chu vi và diện tích hình vuông có cạnh là 7 cm lần lượt là
A. 28cm; 49cm
B. 28cm2; 49cm
C. 49cm; 28cm2
D. 28cm; 49cm2
Trả lời:
Chu vi hình vuông là: 4.7 = 28 (cm)
Diện tích hình vuông là: 72 = 49(cm2)
Đáp án cần chọn là: D
Câu 13. Người ta mở rộng một cái ao hình vuông để được một cái ao hình chữ nhật có chiều dài gấp 2 lần chiều rộng. Sau khi mở rộng, diện tích ao tăng thêm 600m2 và diện tích ao mới gấp 4 lần ao cũ. Hỏi phải dùng bao nhiêu chiếc cọc để đủ rào xung quanh ao mới? Biết rằng cọc nọ cách cọc kia 1m và ở một góc ao người ta để lối lên xuống rộng 3m.
A. 120
B. 117
C. 119
D. 122
Trả lời:
Ta có sơ đồ:
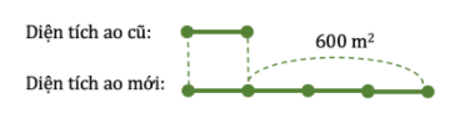
Diện tích ao mới là:
600 : (4 – 1) . 4 = 800 (m2)
Ta chia ao mới thành hai hình vuông có diện tích bằng nhau như hình vẽ. Diện tích một hình vuông là:
800 : 2 = 400 (m2)
Vì 400 = 20 . 20
Cạnh của hình vuông hay chiều rộng của ao mới là 20m
Chiều dài của ao mới là: 20 . 2 = 40 (m)
Chu vi áo mới là:
(40 + 20) . 2 = 120(m)
Số cọc để rào xung quanh ao mới là:
(120 – 3) : 1 = 117 (chiếc)
Đáp án cần chọn là: B
Câu 14. Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m2. Hỏi trước đây sân trường em có diện tích là bao nhiêu m2?
A. 16 m2
B. 32 m2
C. 64 m2
D. 128 m2
Trả lời:
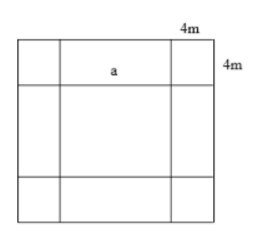
Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
Diện tích 4 hình vuông nhỏ là: 4 . (4 . 4) = 64 m2
Diện tích 4 hình chữ nhật là: 192 - 64 = 128 m2
Diện tích 1 hình chữ nhật là 128 : 4 = 32 m2
Cạnh hình vuông đã cho là: 32 : 4 = 8 m
Diện tích sân trường lúc chưa mở rộng là: 8 . 8 = 64 m2
Đáp án cần chọn là: C
Câu 15. Một thửa ruộng hình chữ nhật có chu vi 200 m. Chiều dài hình chữ nhật hơn hai lần chiều rộng là 10m. Tính diện tích hình chữ nhật đó.
A. 1200 m2
B. 2100 m2
C. 200 m2
D. 100 m2
Trả lời:
Nửa chu vi thửa ruộng là:
200 : 2 = 100 (m)
Chiều rộng của thửa ruộng là:
(100 - 10) : 3 = 30 (m)
Chiều dài của thửa ruộng là:
100 - 30 = 70 (m)
Diện tích hình chữ nhật là:
70 . 30 = 2100 (m2)
Đáp án cần chọn là: B
Câu 16. Tính diện tích mảnh vườn được tạo bởi 1 hình vuông và 1 hình chữ nhật như hình vẽ:
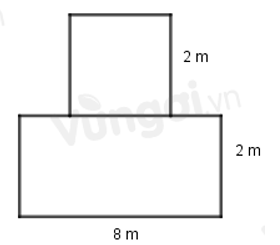
A. 4 m2
B. 16 m2
C. 20 m2
D. 24 m2
Trả lời:
Diện tích phần đất hình vuông là: 22 = 4(m2)
Diện tích phần đất hình chữ nhật là: 8.2 = 16(m2)
Diện tích mảnh vườn là: 4 + 16 = 20(m2)
Đáp án cần chọn là: C
Câu 17. Mỗi viên gạch hoa hình vuông có cạnh 20 cm. Tính chu vi hình vuông ghép bởi 4 viên gạch hoa như hình vẽ dưới đây:
A. 80 cm
B. 160 cm
C. 400 cm
D. 40 cm
Trả lời:
Cạnh của hình vuông là:
20 + 20 = 40 (cm)
Chu vi hình vuông là:
40 . 4 = 160 (cm)
Đáp án cần chọn là: B
Câu 18. Một hồ nước hình vuông cạnh 30 m. Tính chu vi hồ nước đó.
A. 120 m
B. 60 m
C. 120 dm
D. 900 m
Trả lời:
Chu vi hồ nước là:
30 . 4 = 120 (m)
Đáp án cần chọn là: A
Câu 19. Cần bao nhiêu viên gạch hình vuông cạnh 50 cm để lát kín căn phòng có nền là hình vuông có cạnh 12 m?
A. 240 viên
B. 144 viên
C. 24 viên
D. 576 viên
Trả lời:
Đổi 50 cm = 0,5 m.
Diện tích một viên gạch là: 0,5.0,5 = 0,25(m2)
Diện tích căn phòng là: 12.12 = 144(m2)
Số viên gạch để lát kín căn phòng là: 144:0,25 = 576 (viên)
Đáp án cần chọn là: D
Câu 20. Diện tích hình chữ nhật ABCD có chiều dài AB là 15cm và chiều rộng BD là 8cm là:
A. 23cm2
B. 46cm2
C. 120cm2
D. 120cm
Trả lời:
Diện tích hình chữ nhật ABCD là: 15.8 = 120(cm2).
Đáp án cần chọn là: C
B. Lý thuyết Chu vi và diện tích của một số tứ giác đã học
1. Chu vi và diện tích hình chữ nhật
Cho hình chữ nhật có chiều dài là a, chiều rộng là b (như hình vẽ).
Chu vi của hình chữ nhật là: P = (a + b) . 2
Diện tích của hình chữ nhật là: S = a . b
Ví dụ: Cho hình chữ nhật EFGH có EF = GH = 6 cm; EH = FG = 3 cm. Tính chu vi và diện tích hình chữ nhật EFGH.
Hướng dẫn giải
Chu vi hình chữ nhật EFGH là:
(6 + 3) . 2 = 18 (cm)
Diện tích hình chữ nhật EFGH là:
6 . 3 = 18 (cm2).
Vậy hình chữ nhật EFGH có chu vi là 18 cm và diện tích là 18 cm2.
2. Chu vi và diện tích của hình vuông
Cho hình vuông có độ dài một cạnh bằng a (như hình vẽ).
Chu vi hình vuông là: P = 4a.
Diện tích hình vuông là: S = a . a = a2.
Ví dụ: Một mảnh ruộng hình vuông có cạnh bằng 15m. Năng suất lúa là 0,9 kg/m2. Tính sản lượng thu hoạch được trên mảnh ruộng hình vuông.
Hướng dẫn giải
Diện tích mảnh ruộng hình vuông là:
152 = 225 (m2).
Sản lượng thu hoạch được là:
225 : 0,9 = 312,5 (kg).
Vậy sản lượng thu hoạch được trên mảnh ruộng hình vuông là 312,5 kg.
3. Chu vi và diện tích của hình tam giác
Cho tam giác có độ dài ba cạnh lần lượt là a, b, c và chiều cao tương ứng với cạnh a có độ dài là h (như hình vẽ).
Chu vi hình hình tam giác là: P = a + b + c.
Diện tích hình tam giác là: 
Ví dụ: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm, BC = 5 cm. Tính chu vi và diện tích tam giác ABC.
Hướng dẫn giải
Chu vi tam giác ABC là:
3 + 4 + 5 = 12 (cm).
Diện tích tam giác ABC là:
Vậy tam giác ABC có chu vi là 12 cm và diện tích là 6 cm2.
4. Chu vi và diện tích của hình thang
Cho hình thang có độ dài bốn cạnh là a, b, c, d và đường cao h (như hình vẽ).
Chu vi của hình thang là: P = a + b + c + d
Diện tích của hình thang là:
Ví dụ: Tính diện tích hình thang cân có độ dài hai đáy là 5 m và 3,5 m; chiều cao là 4 m.
Hướng dẫn giải
Diện tích hình thang cân là:
Vậy diện tích hình thang cân là 17 cm2.
5. Chu vi và diện tích hình bình hành
Cho hình bình hành có độ dài hai cạnh là a và b, chiều cao tương ứng với một cạnh a có độ dài là h (như hình vẽ).
Chu vi hình bình hành là: P = 2(a + b).
Diện tích hình bình hành là: S = a . h.
Ví dụ: Hình bình hành có độ dài một cạnh là 12 cm và chiều cao tương ứng là 8 cm.
Khi đó, diện tích của hình bình hành là:
12 . 8 = 96 (cm2).
6. Chu vi và diện tích hình thoi
Cho hình thoi có độ dài một cạnh là a, độ dài hai đường chéo của hình thoi là m và n.
Chu vi của hình thoi là: P = 4a.
Diện tích của hình thoi là: 
Ví dụ: Hình thoi có độ dài hai đường chéo là 60 m và 50 m có diện tích là:
7. Chu vi và diện tích của một số hình trong thực tiễn
a) Tính chu vi của một số hình trong thực tiễn:
Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó.
b) Tính diện tích của một số hình trong thực tiễn:
− Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, … thì ta áp dụng công thức và tính.
− Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, …
Ví dụ: Tính chu vi và diện tích hình được tô màu sau:
Hướng dẫn giải
Chu vi của hình đã cho là:
8 + 6 + 5 + 7 + (8 + 5) +1 = 40 (cm).
Chia hình ban đầu thành hai hình như hình vẽ. Khi đó ta có:
Diện tích hình chữ nhật to là:
5 . 7 = 35 (cm2).
Diện tích hình chữ nhật nhỏ là:
8 . (7 – 6) = 8 (cm2).
Diện tích hình ban đầu là:
35 + 8 = 43 (cm2).
Vậy hình được tô màu có chu vi là 40 cm và diện tích là 43 cm2.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
