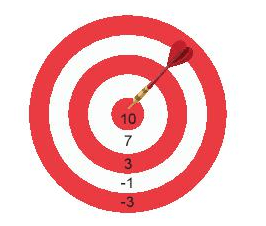
Bài 1. Ba bạn An, Bình, Cường chơi ném tiêu với bia gồm năm vòng như hình vẽ. Kết quả được ghi lại trong bảng sau:

Lời giải

Số điểm của An đạt được là: 

1.10 + 7.2 + 3.0 + (-1).1 + (-3).1

= 10 + 14 + (-1) + (-3)

= 24 + (-1) + (-3) 

= 23 + (-3) 

= 20.

Số điểm bạn Bình đạt được là: 

2.10 + 0.7 + 3.1 + (-1).0 + (-3).2

= 20 + 3 + (-6)

= 23 – 6

= 17.

Số điểm bạn Cường đạt được là:

10.0 + 3.7 + 3.1 + 1.(-1) + (-3).0

= 21 + 3 + (-1) 

= 23.

Vậy bạn Cường đạt điểm cao nhất.

Bài 2. Tính một cách hợp lí

a) (-3).(-17) + 3.(120 – 17);

b) (-8).72 + 8.(-19) – (-8);

c) (-27).1 011 – 27.(-12) + 27.(-1).

Lời giải

a) (-3).(-17) + 3.(120 – 17)

= 3.17 + 3.120 – 3.17

= (3.17 – 3.17) + 3.120

= 0 + 360

= 360.

b) (-8).72 + 8.(-19) – (-8)

= 8.(-72) + 8.(-19) + 8

= 8[(-72) + (-19) + 1]

=8[(-91) + 1]

=8.(-90)

= -720.

c) (-27).1 011 – 27.(-12) + 27.(-1)

= 27.(-1 011) – 27.(-12) + 27.(-1)

= 27.[(-1 011) – (-12) + (-1)]

= 27.(-1 000)

= -27 000.

Bài 3. Tính: 

a) (−3) . 8;

b) (−14) . (−25);

c) (+12) . (−40);

Hướng dẫn giải

a) (−3) . 8 = − (3 . 8) = − 24;

b) (−14) . (−25) = 14 . 25 = 350;

c) (+12) . (−40) = − (12 . 40) = −480.

Bài 4: Tìm x, biết:

30(x + 2) − 6(x − 5) − 22x = 100.

Hướng dẫn giải

30(x + 2) − 6(x − 5) − 22x = 100

(30x + 60) − (6x − 30) − 22x = 100

30x + 60 − 6x + 30 − 22x = 100

30x – 6x − 22x = 100 – 60 − 30

2x = 10

x = 5

Vậy x = 5.

Bài 5: Tìm số nguyên a để 5 ⋮ (a – 1).

Hướng dẫn giải

 Để 5 ⋮ (a – 1) ($a\in \mathrm{\mathbb{Z}}$) thì  a – 1 $\in$ Ư(5) = {−5; −1; 1; 5}.

Ta có bảng sau:

Vậy để 5 ⋮ (a – 1) thì a $\in$ {− 4; 0; 2; 6}.

Bài 6. Thực hiện các phép tính sau:

a) (– 15) . (– 4);                                  b) (– 20) . (– 6);                                  c) 20 . 7.

Lời giải:

a) Ta có: (– 15) . (– 4) = 15 . 4 = 60

b) Ta có: (– 20) . (– 6) = 20 . 6 = 120

c) Ta có: 20 . 7 = 140

Bài 7. Một xí nghiệp mỗi ngày may được 350 bộ quần áo. Khi may theo mốt mới, với cùng khổ vải, số vải dùng để máy một bộ quần áo tăng x (cm) và năng suất không thay đổi. Hỏi mỗi ngày số vải tăng bao nhiêu xăng-ti-mét với:

a) x = 15?                   b) x = – 10?

Lời giải:

Vì mỗi bộ quần áo mốt mới cần thêm x (cm) vải nên 350 bộ quần áo thì cần thêm 350 . x (cm) vải. 

Do đó mỗi ngày số vải tăng 350 . x (cm)

a) Với x = 15, mỗi ngày số vải tăng là 350 . 15 = 5 250 (cm)

b) Với x = – 10, mỗi ngày số vải tăng là 350 . (–10) = – 3 500 (cm)

Nghĩa là số vải giảm đi 3 500 (cm).

Bài 8. Thực hiện các phép tính sau

a) (– 4) . 2 . 6 . 25 . (– 7) . 5

b) 16 . (38 – 2) – 38 . (16 – 1)

Lời giải:

a) Ta có: (– 4) . 2 . 6 . 25 . (– 7) . 5 

= [(– 4) . 25] . (2 . 5) . [6 . (– 7)]

       = (– 100) . 10 . (– 42) 

= (– 1 000) . (– 42)

        = 42 000

b) Ta có: 16 . (38 – 2) – 38 . (16 – 1) 

= 16 . 38 – 16 . 2 – 38 . 16 + 38

       = (16 . 38 – 38 . 16) + 38 – 16 . 2

           = 0 + 38 – 32 = 6

Câu 9. Cho tích 213.3 = 639. Từ đó suy ra nhanh kết quả của các tích sau: (- 213).3; 

A. -639

B. 639

C. 1 278

D. -1 278

Lời giải

Ta có: 213.3 = 639

Từ đó suy ra: 

(- 213).3 = - 639

Đáp án: A

Câu 10. Tích của hai số nguyên âm là số thế nào?

A. là số nguyên âm

B. là số nguyên dương

C. là số 0

D. vừa là số nguyên âm vừa là số nguyên dương

Lời giải

Sau bài này ta sẽ biết được là:

Tích của hai số nguyên âm sẽ là một số nguyên dương.

Đáp án: B

Câu 11. Thực hiện phép tính sau: (-5).4

A. – 20

B. 20

C. 10

D. -10 

Lời giải (-5).4 = -(5.4) = - 20

Đáp án: A

Câu 12. Phép nhân có tính chất gì:

A. Tính chất giao hoán

B. Tính chất kết hợp

C. Tính chất phân phối của phép nhân với phép cộng

D. Cả ba tính chất trên

Lời giải Phép nhân có cả ba tính chất: giao hoán, kết hợp và phân phối của phép nhân với phép cộng.

Đáp án: D

Câu 13. Không thực hiện phép tính, hãy so sánh: (+4).(-8) với 0; 

A. (+4).(-8) ≥ 0  

B. (+4).(-8) > 0

C. (+4).(-8) = 0

D. (+4).(-8) < 0

Lời giải Vì (+4).(- 8) ra kết quả mang dấu âm. Do đó (+4).(- 8) < 0.

Đáp án: D

Câu 14. Thực hiện phép tính: (- 3).(- 2).(- 5). 4;                                             

A. 150

B. 120

C. -120

D. -150

Lời giải (- 3).(- 2) .(- 5) .4 = [(-3).4)].[(-2).(-5)] = (-12).10 =  -120.

Đáp án: C

Câu 15. Một kho lạnh đang ở nhiệt độ , một công nhân cần đặt chế độ làm cho nhiệt độ của kho trung bình cứ mỗi phút giảm đi. Hỏi sau 5 phút nữa nhiệt độ trong kho là bao nhiêu?

A. 2⁰C

B. 10⁰C

C. – 10⁰C

D. – 2⁰C

Lời giải

Cứ mỗi phút giảm 

Sau 5 phút nhiệt độ giảm: 5.2 = 10⁰C

Vậy: Sau 5 phút nữa nhiệt độ trong kho là: 8 – 10 = -2⁰C.

Đáp án: D

Câu 16. Tính giá trị của biểu thức trong mỗi trường hợp sau: 19x với x = - 7;

A. 124

B. -124

C. 133

D. - 133

Lời giải

Thay x = -7 vào 19x, ta được:

19.(-7) = -133.

Vậy với x = -7 thì giá trị biểu thức là -133.

Đáp án: D

Câu 17: Tính $\frac{9}{14}\cdot \frac{-5}{8}\cdot \frac{14}{9}$

A.$\frac{-15}{28}$

B.$\frac{-9}{28}$

C.$\frac{-5}{8}$

D.$\frac{-7}{8}$

Trả lời:

 $\frac{9}{14}\cdot \frac{-5}{8}\cdot \frac{14}{9}=\left(\frac{9}{14}\cdot \frac{14}{9}\right)\cdot \frac{-5}{8}=1.\frac{-5}{8}=\frac{-5}{8}.$

Đáp án cần chọn là: C

Câu 18: Tìm x biết$x:\left(-\frac{2}{5}\right)=\frac{3}{54}$

A.$x=\frac{-1}{27}$

B.$x=\frac{-1}{18}$

C.$x=\frac{-1}{45}$

D.$x=\frac{-1}{9}$

Trả lời:

 $\begin{array}{l}x:\left(-\frac{2}{5}\right)=\frac{3}{54}\\ x=\frac{3}{54}.\left(-\frac{2}{5}\right)\\ x=\frac{1}{18}.\frac{-2}{5}\\ x=\frac{-1}{45}\end{array}$

Đáp án cần chọn là: D

Câu 19: Giá trị nào dưới đây của x thỏa mãn$x:\frac{5}{8}=\frac{-14}{35}\cdot \frac{15}{-42}$

A.$\frac{5}{56}$

B.$\frac{-5}{56}$

C.$\frac{5}{28}$

D.$\frac{-5}{28}$

Trả lời:

 $$\begin{gathered} x:\frac{5}{8}=\frac{-14}{35}\cdot \frac{15}{-42} \\ x:\frac{5}{8}=\frac{-2}{5}.\frac{5}{-14} \\ x:\frac{5}{8}=\frac{1}{7} \\ x=\frac{1}{7}.\frac{5}{8} \\ x=\frac{5}{56} \end{gathered}$$

Đáp án cần chọn là: A

Câu 20: Chọn câu sai.

A. (– 19) . (– 7) > 0     

B. 3 . (– 121) < 0

C. 45 . (– 11) < – 500     

D. 46 . (– 11) < – 500