Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Ước chung. Ước chung lớn nhất, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Ước chung. Ước chung lớn nhất. Mời các bạn đón xem:
Bài tập Toán 6 Ước chung. Ước chung lớn nhất
A. Bài tập Ước chung. Ước chung lớn nhất
Bài 1. Cho hai số a = 132, b = 36.
a) Phân tích a và b ra thừa số nguyên tố.
b) Tìm ƯCLN(a, b) và ƯC(a, b).
Lời giải
a) 132 = 22.3.11; 36 = 22.32.
b) ƯCLN(132, 36) = 22.3 = 12.
ƯC(132, 36) = {1; 2; 3; 4; 6; 12}.
Bài 2. Các phân số sau đã tối giản chưa? Nếu chưa hãy rút gọn phân số đến phân số tối giản.

Lời giải
Tất cả các phân số đã cho đều chưa tối giản.
a) Vì 15050 nên ƯCLN(150, 50) = 50.
Để rút gọn phân số ta chia cả tử và mẫu cho 50, ta được:
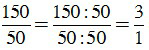 = 3
= 3
b) Ta có: 90 = 2.32.5, 27 = 33.
ƯCLN(90,27) =32 = 9.
Để rút gọn phân số ta chia cả tử và mẫu cho 9, ta được:
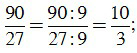
c) Ta có: 34 = 2.17, 255 = 3.5.17.
ƯCLN(34, 255) = 17.
Để rút gọn phân số ta chia cả tử và mẫu cho 17, ta được:
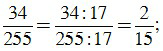
d) Ta có: 88 = 23.11, 121 = 112
ƯCLN(88, 121) = 11.
Để rút gọn phân số ta chia cả tử và mẫu cho 11, ta được:
 .
.
Bài 3: Tìm các ước chung lớn hơn 20 của 144 và 192.
Hướng dẫn giải
UCLN(144, 192) = 48.
Ước của 48 = {1; 2; 3; 4; 6; 8; 12; 24; 48}
Các ước của 48 lớn hơn 20 là 24 và 48.
Vậy các ước chung lớn hơn 20 của 144 và 192 là 24 và 48.
Bài 4. Một bác thợ mộc muốn làm kệ để đồ từ hai tấm gỗ dài 18 dm và 30 dm. Bác muốn cắt hai tấm gỗ này thành các thanh gỗ có cùng độ dài mà không để thừa mẩu gỗ nào. Em hãy giúp bác thợ mộc tìm độ dài lớn nhất có thể của mỗi thanh gỗ được cắt.
Hướng dẫn giải
Độ dài lớn nhất các thanh gỗ được cắt chính là ƯCLN của 18 và 30.
Ta có: 18 = 2 . 32; 30 = 2 . 3. 5.
Các thừa số nguyên tố chung là 2 và 3.
Số mũ lớn nhất của 2 là 1 và của 3 là 1.
Do đó ƯCLN(18; 30) = 2. 3 = 6.
Vậy độ dài lớn nhất có thể của các thanh gỗ được cắt là 6 dm.
Bài 5. Tìm hai số tự nhiên a, b, biết rằng: a + b = 162 và ƯCLN(a, b) = 18.
Lời giải
Giả sử a ≤ b.
Ta có: a + b = 162, ƯCLN(a, b) = 18.
Khi đó a ⋮ 18, b ⋮ 18.
Đặt a = 18m; b = 18n với ƯCLN(m, n) = 1, m ≤ n.
Từ a + b = 162 nên 18(m + n) = 162 suy ra m + n = 9.
Ta có ba cặp số (m; n) thỏa mãn m + n = 9 và ƯCLN(m, n) = 1, m ≤ n là:
(1; 8); (2; 7); (4; 5) (loại cặp số (3; 6) vì ƯCLN(3; 6) = 3 ≠ 1).
Ta có bảng sau:
|
m |
1 |
2 |
4 |
|
n |
8 |
7 |
5 |
|
a |
18 |
36 |
72 |
|
b |
144 |
126 |
90 |
Vậy các bộ hai số tự nhiên cần tìm là: (18; 144); (36; 126); (72; 90).
Bài 6. Tìm ƯCLN(126, 150). Từ đó hãy tìm tất cả các ước chung của 126 và 150.
Lời giải:
+ Ta có:


Do đó: 126 = 2 . 3 . 3 . 7 = 2 . 32 . 7
150 = 2 . 3 . 5 . 5 = 2 . 3 . 52
Các thừa số nguyên tố chung của 126 và 150 là 2 và 3
Số 2 có số mũ nhỏ nhất là 1; số 3 có số mũ nhỏ nhất là 1.
Do đó: ƯCLN(126, 150) = 21 . 31 = 2 . 3 = 6
Lại có 6 có các ước là 1; 2; 3; 6.
Ước chung của 126 và 150 là ước của ƯCLN(126, 150) là 1; 2; 3; 6
Hay ƯC(126, 150) =
Vậy ƯCLN(126, 150) = 6; ƯC(126, 150) = .
Bài 7. Rút gọn phân số 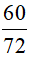 về phân số tối giản.
về phân số tối giản.
Lời giải:
Các phân số được gọi là tối giản khi phân số đó có tử và mẫu là hai số nguyên tố cùng nhau. Vậy để rút gọn các phân số (chưa phải là phân số tối giản) thì ta đi tìm ƯCLN của tử số và mẫu số, rồi lấy cả tử và mẫu chia cho ƯCLN của cả hai thì ta được phân số tối giản.
Rút gọn phân số 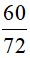
Ta có:
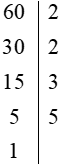
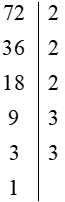
Do đó: 60 = 22 . 3 . 5 và 72 = 23 . 32
Các thừa số nguyên tố chung là 2 và 3, số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1
Suy ra ƯCLN(60, 72) = 22 . 31 = 4 . 3 = 12
Vậy 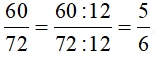
Bài 8. Một căn phòng hình chữ nhật có chiều dài là 680 cm và chiều rộng là 480 cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch đó có độ dài lớn nhất bằng bao nhiêu?
Lời giải:
Gọi độ dài của viên gạch hình vuông là x 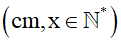 .
.
Để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì x phải là ước chung của chiều dài và chiều rộng.
Hay 680 ⋮ x và 480 ⋮ x
Do đó x ∈ ƯC(680, 480)
Để x lớn nhất thì x = ƯCLN(680, 480)
Ta có: 680 = 23 . 5 . 17; 480 = 25 . 3 . 5
Khi đó: x = ƯCLN(680, 480) = 23 . 5 = 40.
Vậy để lát kín căn phòng đó mà không có viên gạch nào bị cắt xén thì độ dài lớn nhất của viên gạch là 40 cm.
Câu 9. Cho tập ƯC(24; 28) = {1; 2; 4}. Vậy ƯCLN(24; 28) là:
A. 1;
B. 2;
C. 4;
D.24.
Lời giải
Tập ƯC(24; 28) = {1; 2; 4}.
Mà 4 là số lớn nhất trong tập này nên ƯCLN(24, 28) = 4.
Đáp án: C
Câu 10. Tìm ƯCLN(72, 63, 1):
A. 63;
B. 72;
C. 9;
D. 1.
Lời giải
Ta có ƯCLN(a, b, 1) = 1 với a, b là các số tự nhiên.
Vậy ƯCLN(72, 63, 1) = 1.
Đáp án: D
Câu 11. Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta thực hiện:
A. Tìm ƯCLN của các số đó. Khi đó tập hợp ước chung của các số đó chính là tập hợp ước của ƯCLN.
B. Viết tập hợp các ước của các số đó ra. Tìm trong số đó các phần tử chung. Tập các phần tử đó chính là tập hợp ước chung của các số đó.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Lời giải
Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta có hai cách để tìm như sau:
Cách 1.
- Tìm ƯCLN của các số đó.
- Tìm các ước của ƯCLN đó.
- Kết luận tập hợp ƯC là tập các ước của ƯCLN.
Cách 2.
- Liệt kê tập hợp ước của các số.
- Tìm các phần tử chung của các tập hợp đó.
- Tập hợp ƯC là tập các phần tử chung đó.
Vậy cả A và B đều đúng.
Đáp án: D
Câu 12. Nếu 9 là số lớn nhất sao cho a ⋮ 9 và a ⋮ 9 thì 9 là ………… của a và b. Chọn câu trả lời đúng nhất.
A. ước;
B. ước chung;
C. ước chung lớn nhất;
D. bội.
Lời giải
Nếu 9 là số lớn nhất sao cho a ⋮ 9 và b ⋮ 9 thì 9 là ước chung lớn nhất của a và b.
Đáp án: C
Câu 13. Nếu a ⋮ 7 và a ⋮ 7 thì 7 là ……………… của a và b.
A. ước
B. ước chung;
C. ước chung lớn nhất;
D. bội.
Lời giải
Nếu a ⋮ 7 và b ⋮ 7 thì 7 là ước chung của a và b.
Đáp án: B
Câu 14. Cho tập Ư(8) = {1; 2; 4; 8} và Ư(20) = {1; 2; 4; 5; 10; 20}. Tập hợp ƯC(8; 20) là:
A. ƯC(8; 20) = {1; 2; 4}.
B. ƯC(8;20) = {1; 2}.
C. ƯC(8; 20) = {1;4}.
D. ƯC(8; 20) = {2;4}.
Lời giải
Các phần tử chung của tập Ư(8) và Ư(20) là: 1; 2; 4.
Do đó ƯC(8; 20) = {1;2;4}.
Đáp án: A
Câu 15. 8 là ước chung của
A. 12 và 32
B. 24 và 56
C. 14 và 48
D. 18 và 24
Trả lời:
24:8 = 3;
56:8 = 7
=> 8 là ước chung của 24 và 56.
Đáp án cần chọn là: B
Câu 16. Tìm ƯCLN(18; 60)
A. 6
B. 30
C. 12
D. 18
Trả lời:
Ta có:
18 = 2.32; 60 = 22.3.5
Nên ƯCLN(18;60) = 2.3 = 6
Đáp án cần chọn là: A
Câu 17: Chọn khẳng định đúng:
A.Mọi số tự nhiên đều có ước chung với nhau.
B.Mọi số tự nhiên đều có ước là 0
C.Số nguyên tố chỉ có đúng 1 ước là chính nó
D.Hai số nguyên tố khác nhau thì không có ước chung
Lời giải
+ Đáp án A: Đáp án này đúng vì mọi số tự nhiên đều có ước chung là 1
+ Đáp án B: Đáp án này sai, vì 0 không là ước của bất kì một số nào cả
+ Đáp án C: Đáp án này sai, vì số nguyên tố có 2 ước là 1 và chính nó
+ Đáp án D: Đáp án này sai, vì 2 số nguyên tố có ước chung là 1
Chọn đáp án A.
Câu 18: ƯCLN của a và b là:
A. bằng b nếu a chia hết cho b
B.bằng a nếu a chia hết cho b
C.ước chung nhỏ nhất của a và b
D.hiệu của 2 số a và b
Lời giải
Nếu a chia hết cho b thì b là ước của a.
Mà b cũng là ước của b nên là ước chung của a và b.
Hơn nữa b là ước lớn nhất của b nên ƯCLN (a, b) = b.
Vậy ƯCLN của a và b là bằng b nếu a chia hết cho b.
Chọn đáp án A.
Câu 19: Số tự nhiên a lớn nhất thỏa mãn 90 ⁝ a và 135 ⁝ a là:
A. 15
B. 30
C. 45
D. 60
Lời giải
Vì 90 ⁝ a nên a là ước của 90
và 135 ⁝ a nên a là ước của 135
Suy ra a là ước chung của 90 và 135.
Vì a là số lớn nhất thỏa mãn điều kiện trên nên a = ƯCLN (90, 135).
Phân tích các số 90 và 135 ra thừa số nguyên tố, ta được:
90 = 2 . 32 . 5
135 = 33 . 5
Vậy ƯCLN(90, 135) = 32 . 5 = 45 hay a = 45.
Chọn đáp án C.
Câu 20: Trong hai số sau, hai số nào là hai số nguyên tố cùng nhau:
A. 2 và 6
B. 3 và 10
C. 6 và 9
D. 15 và 33
Lời giải
Ta có:
ƯC(2, 6) = {1; 2} nên ƯCLN(2, 6) = 2
ƯC(3, 10) = {1} nên ƯCLN(3, 10) = 1
ƯC(6, 9) = {1; 3} nên ƯCLN(6, 9) = 3
ƯC(15, 33) = {1; 3} nên ƯCLN(15, 33) = 3
Chú ý: Hai số gọi là nguyên tố cùng nhau nếu chúng có ước chung lớn nhất là 1.
Vậy 3 và 10 là hai số nguyên tố cùng nhau.
Chọn đáp án B
B. Lý thuyết Ước chung. Ước chung lớn nhất
I. Ước chung và ước chung lớn nhất
1. Ước chung: Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.
Quy ước: Viết tắt ước chung là ƯC.
Kí hiệu: Tập hợp các ước chung của a và b là ƯC(a, b).
Ví dụ: Ta có:
Các ước của 8 là: 1, 2, 4, 8
Các ước của 12 là: 1, 2, 3, 4, 6, 12
Do đó các ước chung của 8 và 12 là: 1, 2, 4.
Vậy ƯC(8, 12) = {1; 2; 4} .
Chú ý: Số tự nhiên n được gọi là ước chung của ba số a, b, c nếu n là ước của cả ba số a, b, c.
Ví dụ: Số 14 chia hết cho 7 nên 7 là ước của 14, 21 chia hết cho 7 nên 7 là ước của 21, 49 chia hết cho 7 nên 7 là ước của 49. Vậy 7 là ước chung của ba số 14, 21, 49.
2. Ước chung lớn nhất: Số lớn nhất trong các ước chung của hai số a và b được gọi là ước chung lớn nhất của a và b.
Quy ước: Viết tắt ước chung lớn nhất là ƯCLN.
Kí hiệu: ước chung lớn nhất của a và b là ƯCLN(a, b).
Ví dụ: Trong các ước chung của 8 và 12 là 1, 2, 4 thì 4 là số lớn nhất nên 4 là ước chung lớn nhất của 8 và 12. Ta viết ƯCLN(8, 12) = 4.
3. Tìm ước chung của hai số khi biết ƯCLN của hai số đó
Ước chung của hai số là ước của ước chung lớn nhất của chúng.
Ví dụ: Biết ƯCLN (a, b) = 60. Tìm tất cả các số có hai chữ số là ước chung của a và b.
Lời giải:
Vì ước chung của a và b đều là ước của ƯCLN (a, b) = 60 nên tất cả các số có hai chữ số là ước chung của a và b là: 10, 12, 15, 20, 30, 60.
II. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Các bước tìm ƯCLN bằng cách phân tích ra thừa số nguyên tố:
Bước 1. Phân tích mỗi số ra thừa số nguyên tố
Bước 2. Chọn ra các thừa số nguyên tố chung
Bước 3. Với mỗi thừa số nguyên tố chung, ta chọn lũy thừa với số mũ nhỏ nhất
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm.
Ví dụ: Tìm ƯCLN(54, 90).
+ Phân tích các số ra thừa số nguyên tố
54 = 2.33
90 = 2.32.5
Thừa số nguyên tố chung là 2 và 3. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2.
Vậy ƯCLN (54, 90) = 2.32 = 18.
Chú ý:
+ Nếu hai số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.
+ Nếu 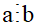 thì ƯCLN(a, b) = b. Chẳng hạn, ƯCLN(48, 16) = 16.
thì ƯCLN(a, b) = b. Chẳng hạn, ƯCLN(48, 16) = 16.