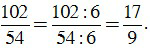Với giải sách bài tập Toán 6 Bài 11: Ước chung. Ước chung lớn nhất sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 11: Ước chung. Ước chung lớn nhất
Bài 2.33 trang 39 sách bài tập Toán lớp 6 Tập 1: Hãy tìm tập hợp Ư(105), Ư(140) và ƯC(105, 140).
Lời giải:
+) Phân tích 105 ra thừa số nguyên tố: 105 = 3. 5. 7
Vì 105 chia hết cho các số: 1; 3; 5; 7; 15; 21; 35; 105
Do đó: Ư(105) = {1; 3; 5; 7; 15; 21; 35; 105}
+) Phân tích 140 ra thừa số nguyên tố: 105 = . 5. 7
Vì 140 chia hết cho các số: 1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140
Do đó: Ư(140) = {1; 2; 4; 5; 7; 10; 14; 20; 28; 35; 70; 140}.
Khi đó ƯC(105, 140) = {1; 5; 7; 35}.
Bài 2.34 trang 39 sách bài tập Toán lớp 6 Tập 1: Tìm ƯCLN của:
a) 35 và 105;
b) 15; 180 và 165.
Lời giải:
a) Vì 105 35 nên ƯCLN(35, 105) = 35.
Vậy ƯCLN(35, 105) = 35.
b) Vì 180 15; 165 15 nên ƯCLN(15, 180, 165) = 15.
Vậy ƯCLN(15, 180, 165) = 15.
a) 72 và 90;
b) 200; 245 và 125.
Lời giải:
a)
Phân tích các số 72 và 90 ra thừa số nguyên tố:
72 = 23.32; 90 = 2.32.5;
+) Ta chọn ra các thừa số nguyên tố chung là: 2 và 3.
+) Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2. Khi đó:
ƯCLN(72; 90) = 2. 32 = 18. Ta được ƯC(72; 90) = Ư(18) = {1; 2; 3; 6; 9; 18}
Vậy ƯCLN(72; 90) = 18 và ƯC(72; 90) = {1; 2; 3; 6; 9; 18}.
b) Phân tích các số 200; 245 và 125 ra thừa số nguyên tố:
;200 = 23.52 245 = 5.72 125 = 53
+) Ta chọn ra thừa số nguyên tố chung là: 5.
+) Số mũ nhỏ nhất của 5 là 1
ƯCLN(200; 245; 125) = 5. Ta được ƯC(200; 245; 125) = Ư(5) = {1; 5}
Vậy ƯCLN(200; 245; 125) = 5 và ƯC(200; 245; 125) = {1; 5}.
Bài 2.36 trang 39 sách bài tập Toán lớp 6 Tập 1: Điền các từ thích hợp vào chỗ chấm:
a) Nếu a ⁝ 7 và b ⁝ 7 thì 7 là……. của a và b.
b) Nếu 9 là số lớn nhất sao cho a ⁝ 9 và b ⁝ 9 thì 9 là …….. của a và b.
Lời giải:
a) Nếu a ⁝ 7 và b ⁝ 7 thì 7 là ước chung của a và b.
b) Nếu 9 là số lớn nhất sao cho a ⁝ 9 và b ⁝ 9 thì 9 là ước chung lớn nhất của a và b.
Lời giải:
Gọi x là số chiếc bút trong mỗi hộp bút chì màu (chiếc, x ∈ N*; x > 2)
Theo bài ra ta có: 25 chia hết cho x; 20 chia hết cho x
Suy ra x là ƯC(25; 20)
Ta có: 25 = 52; 20 = 22.5
ƯCLN(25; 20) = 5
ƯC(25; 20) = Ư(5) = {1; 5} nên x ∈ {1;5}
Mà x > 2 nên x = 5.
Vậy mỗi hộp bút chì màu có 5 chiếc.
Chẳng hạn, các ước của 6 (không kể chính nó) là 1; 2; 3; ta có: 1 + 2 + 3 = 6.
Vậy 6 là số hoàn hảo. Em hãy chỉ ra trong các số 10; 28; 496; số nào là số hoàn hảo.
Cho đến năm 2018, người ta mới tìm được 51 số hoàn hảo. Số hoàn hảo thứ 51 là số có 49 724 095 chữ số.
Lời giải:
+) Các ước của 10 (không kể chính nó) là 1; 2; 5 và 1 + 2 + 5 = 8 ≠ 10 nên 10 không là số hoàn hảo.
+) Các ước của 28 (không kể chính nó) là: 1; 2; 4; 7; 14 và 1 + 2 + 4 + 7 + 14 = 28 nên 28 là số hoàn hảo.
+) Các ước của 496 (không kể chính nó) là 1; 2; 4; 8; 16; 31; 62; 124; 248 và 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496 nên 496 là số hoàn hảo.
Vậy trong các số trên có 28 và 496 là số hoàn hảo.
Lời giải:
Vì 480 ⁝ a và 720 ⁝ a nên a là ước chung của 480 và 720
Mà a lớn nhất nên a = ƯCLN(480; 720)
Ta có:
480 = 25.3.5
720 = 24.32.5
+) Ta chọn ra các thừa số nguyên tố chung là: 2; 3 và 5.
+) Số mũ nhỏ nhất của 2 là 4, số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1
ƯCLN(480; 720) = 24.3. 5 = 240.
Vậy số tự nhiên a lớn nhất là 240.
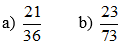
Lời giải:
a) Ta có:
21 = 3.7; 36 = 22.32
+) Thừa số nguyên tố chung là 3 với số mũ nhỏ nhất là 1 nên ƯCLN(21, 36) = 3.
Do đó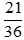 
không là phân số tối giản.
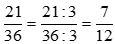. Ta được 
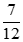là phân số tối giản vì ƯCLN(7, 12) = 1
b) Ta có:
23 = 23; 73 = 73
+) Không có thừa số nguyên tố chung nên ƯCLN(23, 73) = 1.
Do đó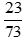 
là phân số tối giản.
Lời giải:
Giả sử cặp số cần tìm là a và b với a,b ≠ 0 . Vì ƯCLN của hai số đó là 17 ⇒ a và b chia hết cho 17 hay a và b đều là bội của 17.
B(17) = {0; 17; 34; 51; 68; …}
Vì các cặp số tự nhiên khác 0, không vượt quá 60 nên a và b thuộc {17; 34; 51}
Do đó ta có các cặp số (a; b) là (17; 34); (17; 51); (34; 51)
Thử lại: ƯCLN(17; 34) = 17 nên (17; 34) thỏa mãn
ƯCLN(17; 51) = 17 nên (17; 51) thỏa mãn
ƯCLN(34; 51) = 17 nên (34; 51) thỏa mãn
Vậy các cặp số cần tìm là (17; 34); (17; 51); (34; 51)
Lời giải:
Vì ƯCLN(a, b) = 16 ⇒ a và b là bội của 16, ta giả sử a = 16m; b = 16n với
ƯCLN(m, n) = 1 và do các số tự nhiên khác 0 nên m,n ∈ N*
Ta có a + b = 96 nên 16. m + 16. n = 96
16. (m + n) = 96
m + n = 96: 16
m + n = 6
Ta có bảng sau:
|
m |
1 |
2 |
3 |
4 |
5 |
|
n |
5 |
4 |
3 |
2 |
1 |
|
ƯCLN(m, n) = 1 |
TM |
KTM |
KTM |
KTM |
TM |
+) Với m = 1; n = 5 ta được a = 1. 16 = 16; b = 5. 16 = 80
+) Với m = 5; n = 1, ta được a = 5. 16 = 80; b = 1. 16 = 16
Vậy các cặp số (a; b) thỏa mãn là (16; 80); (80; 16)
Lời giải:
Vì ƯCLN của hai số đó là 8 nên hai số đó là bội của 8, ta giả sử a = 8m; b = 8n với ƯCLN(m, n) = 1 và do cặp số tự nhiên khác 0 nên m,n ∈ N*
Tích của hai số là 384 nên a.b = 384 hay 8m. 8n = 384
64. m. n = 384
m. n = 384: 64
m. n = 6
Ta có 6 = 1. 6 = 2. 3
Do đó (m; n) ∈ {(1;6);(6;1);(2;3);(3;2)}
Ta có bảng sau:
|
m |
1 |
6 |
2 |
3 |
|
n |
6 |
1 |
3 |
2 |
|
a = 8m |
8 |
48 |
16 |
24 |
|
b = 8n |
48 |
8 |
24 |
16 |
Vậy các cặp số tự nhiên thỏa mãn đề bài là (8; 48); (48; 8); (16; 24); (24; 16).
Lý thuyết Ước chung. Ước chung lớn nhất
1. Ước chung và ước chung lớn nhất
Ước chung của hai hay nhiều số là ước của tất cả các số đó.
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
Ta kí hiệu:
ƯC(a, b) là tập hợp các ước chung của a và b.
ƯCLN(a, b) là ước chung lớn nhất của a và b.
Ví dụ 1.
a) Tìm ước chung của 24 và 60.
b) Tìm ƯCLN (24; 60).
Lời giải
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30}
a) ƯC(24; 30) = {1; 2; 3; 6}
b) ƯCLN(24; 30) = 6.
Nhận xét:
- Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.
Nếu a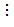 
b thì ƯCLN(a, b) = b.
- Số 1 chỉ có 1 ước là 1. Do đó với mọi số tự nhiên a và b, ta có:
ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.
Ví dụ 2.
a) Tìm ƯCLN(180, 18)
Vì 180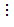 
18 nên ƯCLN(180, 18) = 18.
b) Tìm ƯCLN(13, 1)
Ta có: ƯCLN(13, 1) = 1.
2. Cách tìm ước chung lớn nhất
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:
Bước 1: Phân tích các số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Ví dụ 3. Cách tìm ƯCLN(140, 168)
Ta có: 140 = 22.5.7; 168 = 23.3.7.
Các thừa số chung: 2, 7.
Vậy ƯCLN(140, 168) = 22.7 = 4.7 = 28.
3. Rút gọn về phân số tối giản
Vận dụng ƯCLN để rút gọn về phân số tối giản
Ta rút gọn phân số bằng cách chia cả tử và mẫu của phân số đó cho một ước chung khác 1 (nếu có).
Phân số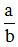 
được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
Ví dụ 4. Rút gọn các phân số sau về phân số tối giản
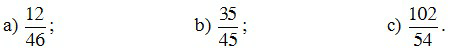
Lời giải
a) ƯCLN(12, 46) = 2.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 12 và 46, ta được:
;
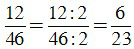b) ƯCLN(35,45) = 5.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 35 và 45, ta được:
;
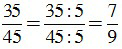c) ƯCLN(102, 54) = 6.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 102 và 54, ta được:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
