Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Quan hệ chia hết và tính chất, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Quan hệ chia hết và tính chất. Mời các bạn đón xem:
Bài tập Toán 6 Quan hệ chia hết và tính chất
A. Bài tập Quan hệ chia hết và tính chất
Bài 1. Tìm các số tự nhiên x, y sao cho:
a) x ∈ B(12) và 10 < x < 40.
b) y ∈ Ư(20) và y ≥ 5 .
Lời giải
a) Ta có: B(12) = {0; 12; 24; 36; 48; …}
⇒ x ∈ {0; 12; 24; 36; ...}
Mà 10 < x < 40 nên x ∈ {12; 24; 36}.
Vậy x ∈ {12; 24; 36}.
b) Ta có: Ư(20) = {1; 2; 4; 5; 10; 20}
⇒ y ∈ {1; 2; 4; 5; 10; 20}
Mà y ≥ 5 nên y ∈ {5; 10; 20}.
Bài 2. Lớp 6A có 36 học sinh, cô giáo muốn chia đều số học sinh của lớp thành các nhóm để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở:
|
Số nhóm |
Số người ở một nhóm |
|
3 |
|
|
|
9 |
|
6 |
|
|
|
4 |
|
12 |
|
Lời giải
Nếu số nhóm là 3 thì số người ở một nhóm là: 36:3 = 12 (người).
Nếu số người ở một nhóm là 9 thì số nhóm là: 36:9 = 4 (nhóm).
Nếu số nhóm là 6 thì số người ở một nhóm là: 36:6 = 6 (người).
Nếu số người ở một nhóm là 4 thì số nhóm là: 36:4 = 9 (người).
Nếu số người ở một nhóm là 3 thì số nhóm là: 36:3 = 12 (nhóm).
Ta có bảng sau:
|
Số nhóm |
Số người ở một nhóm |
|
3 |
12 |
|
4 |
9 |
|
6 |
6 |
|
9 |
4 |
|
12 |
3 |
Bài 3.
a) Tìm m thuộc tập {21; 22; 23; 24; 25; 26}, biết 56 – m chia hết 7;
b) Tìm n thuộc tập {18; 20; 22; 24; 26; 28; 30}, biết 36 + n không chia hết cho 6.
Lời giải
a) Vì 56 chia hết cho 7 để 56 – m chia hết cho 7 thì m phải là một số chia hết cho 7.
Mà m thuộc tập {21; 22; 23; 24; 25; 26}
Suy ra m = 21.
Vậy m = 21.
b) Vì 36 chia hết cho 6 nên để 36 + n không chia hết cho 6 thì n phải không chia hết cho 6.
Mà n thuộc tập {18; 20; 22; 24; 26; 28; 30}.
Suy ra n thuộc {20; 22; 26; 28}.
Vậy n ∈ {20; 22; 26; 28}.
Bài 4. a) Tìm các bội nhỏ hơn 40 của 9.
b) Tìm tất cả các ước của 25.
Lời giải:
a) Để tìm các bội của 9, ta lần lượt nhân 9 với các số 0, 1, 2, 3, 4, 5,… được 0, 9, 18, 27, 36, 45,…
Các bội của 9 là 0, 9, 18, 27, 36, 45,…
Vì cần tìm các bội nhỏ hơn 40 của 9 nên các số thỏa mãn yêu cầu là: 0, 9, 18, 27, 36.
Vậy các bội nhỏ hơn 40 của 9 là: 0, 9, 18, 27, 36.
b) Để tìm các ước của 25, ta thực hiện phép chia 25 cho các số tự nhiên từ 1 đến 25. Các phép chia hết là: 25 : 1 = 25; 25 : 5 = 5; 25 : 25 = 1
Vậy các ước của 25 là 1, 5 và 25.
Bài 5. Không tính giá trị biểu thức, hãy giải thích tại sao A = 36 . 234 + 217 . 24 – 54 . 13 chia hết cho 6.
Lời giải:
Ta có: 36 : 6 = 6; 24 : 6 = 4; 54 : 6 = 9.
Nên các số 36; 24; 54 đều là các số chia hết cho 6, áp dụng tính chất chia hết của một tích ta có:
36 . 234; 217 . 24; 54 . 13 đều là các tích chia hết cho 6.
Khi đó: A = 36 . 234 + 217 . 24 – 54 . 13 chia hết cho 6.
(Theo tính chất chia hết của một tổng và tính chất chia hết của một hiệu).
Câu 6. Hãy tìm tất cả các ước nhỏ hơn hoặc bằng 10 của 30.
A. 1; 2; 3; 5; 10.
B. 1; 3; 5; 6; 10.
C. 1; 2; 5; 6; 10.
D. 1; 2; 3; 5; 6; 10.
Lời giải
Lần lượt chia 30 cho các số tự nhiên từ 1 đến 30 ta thấy 30 chia hết cho: 1; 2; 3; 5; 6; 10; 25; 30.
Các ước nhỏ hơn hoặc 10 là: 1; 2; 3; 5; 6; 10.
Đáp án: D
Câu 7. Cho hai số tự nhiên a và b (b ≠ 0). Nếu có số tự nhiên k sao cho a = kb thì:
A. a chia hết cho b.
B. b chia hết cho a.
C. A và B đều đúng.
D. A và B đều sai.
Lời giải Cho hai số tự nhiên a và b (b ≠ 0). Nếu có số tự nhiên k sao cho a = kb thì ta nói a chia hết cho b.
Đáp án: A
Câu 8. Nếu a chia hết cho b, ta nói …:
A. b là ước của a.
B. a là bội của b.
C. A và B đều đúng.
D. A và B đều sai.
Lời giải Nếu a chia hết cho b, ta nói b là ước của a và a là bội của b. Do đó cả A và B đều đúng.
Đáp án: C
Câu 9. Tìm tập hợp M là ước của 24.
A. M = {1; 2; 3; 4; 8; 12; 24}.
B. M = {1; 2; 3; 4; 6; 8; 24}.
C. M = {1; 2; 4; 6; 8; 12; 24}.
D. M = {1; 2; 3; 4; 6; 8; 12; 24}.
Lời giải
Để tìm ước của 24, ta lấy 24 chia lần lượt cho các số tự nhiên từ 1 đến 24, ta thấy 24 chia hết cho 1; 2; 3; 4; 6; 8; 12; 24.
Vậy M = {1; 2; 3; 4; 6; 8; 12; 24}.
Đáp án: D
Câu 10: Tập hợp các số tự nhiên x thỏa mãn 6 ⁝ (x – 2) là:
A. {1; 2; 3; 6}
B. {3; 6}
C. {5; 8}
D. {3; 4; 5; 8}
Lời giải
Vì 6 ⁝ (x – 2) nên x – 2 là ước của 6.
Mà các ước của 6 là: 1, 2, 3, 6.
Nên ta có các trường hợp sau:
• TH1: x – 2 = 1
Suy ra x = 1 + 2 = 3 (t/m)
• TH2: x – 2 = 2
Suy ra x = 2 + 2 = 4 (t/m)
• TH3: x – 2 = 3
Suy ra x = 3 + 2 = 5 (t/m)
• TH4: x – 2 = 6
Suy ra x = 6 + 2 = 8 (t/m)
Vậy tập hợp các số tự nhiên x thỏa mãn yêu cầu bài toán là: {3; 4; 5; 8}.
Chọn đáp án D.
Câu 11: Viết tập hợp A các số tự nhiên n sao cho n + 5 là ước của 12.
A. A = {1; 2; 3; 4; 6; 12}
B. A = {1; 7}
C. A = {1; 2; 3; 4; 6}
D. A = {1; 2; 3; 4}
Lời giải
Vì n là số tự nhiên và n + 5 là ước của 12 nên n + 5 > 5
Ta tìm được các ước của 12 là: 1, 2, 3, 4, 6, 12
Mà n + 5 là ước của 12 và n + 5 > 5 nên n + 5 chỉ có thể bằng 6 hoặc bằng 12.
Nên ta có 2 trường hợp sau:
• TH1: n + 5 = 6
Suy ra n = 6 – 5 = 1 (t/m)
• TH2: n + 5 = 12
Suy ra n = 12 – 5 = 7 (t/m)
Vậy n = 1, n = 7, do đó ta viết tập hợp A = {1; 7}.
Chọn đáp án B.
Câu 12: Khi chia số tự nhiên a cho 12, ta được số dư là 8. Khẳng định nào sau đây đúng?
A. a chia hết cho 6
B. a chia hết cho 4
C. a chia hết cho 3
D. Cả A, B, C đều đúng
Lời giải
Số tự nhiên a chia cho 12 được số dư là 8 nên a = 12k + 8 (với k ∈ N)
Ta có: 12 : 4 = 3, 8 : 4 = 2 nên 12 và 8 đều chia hết cho 4.
Do đó: 12k cũng chia hết cho 4 (theo tính chất chia hết của một tích)
Khi đó 12k + 8 chia hết cho 4 (theo tính chất chia hết của một tổng)
Vậy a chia hết cho 4.
Chọn đáp án B.
Câu 13: Tìm số tự nhiên x, biết x là bội của 10 và 70 < x < 90.
A. x = 70
B. x = 80
C. x = 85
D. x = 90
Lời giải
Vì x là bội của 10 nên x chia hết cho 10.
Lại có 70 < x < 90, nên x là số tự nhiên lớn hơn 70 và nhỏ hơn 90, là các số từ 71 đến 89, trong đó, ta thấy chỉ có số 80 chia hết cho 10 vì 80 : 10 = 8.
Vậy x = 80.
Chọn đáp án B.
B. Lý thuyết Quan hệ chia hết và tính chất
I. Quan hệ chia hết
1. Khái niệm về chia hết
Cho hai số tự nhiên a và b (b # 0) .
Nếu có số tự nhiên q sao cho a = b . q thì ta nói a chia hết cho b.
Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.
Ví dụ: 42 = 6 . 7 nên 42 chia hết cho 6.
Khi đó ta gọi 42 là bội của 6 và 6 là ước của 42.
Lưu ý:
+ Nếu số dư trong phép chia a cho b bằng 0 thì a chia hết cho b, kí hiệu là 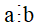 .
.
+ Nếu số dư trong phép chia a cho b khác 0 thì a không chia hết cho b, kí hiệu là 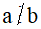 .
.
Ví dụ:
+ 4 chia hết cho 2, kí hiệu là
+ 5 không chia hết cho 2, kí hiệu là
Lưu ý: Với a là số tự nhiên khác 0 thì:
+ a là ước của a;
+ a là bội của a;
+ 0 là bội của a;
+ 1 là ước của a.
Ví dụ:
0 và 7 là hai bội của 7.
1 và 12 là hai ước của 12.
2. Cách tìm bội và ước của một số
2.1 Cách tìm bội của một số
Để tìm các bội của n(n∈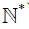 ) ta có thể lần lượt nhân n với 0, 1, 2, 3, …. Khi đó, các kết quả nhận được đều là bội của n.
) ta có thể lần lượt nhân n với 0, 1, 2, 3, …. Khi đó, các kết quả nhận được đều là bội của n.
Ví dụ: Tìm các bội nhỏ hơn 20 của 7.
Lời giải:
Để tìm các bội của 7 ta lần lượt nhân 7 với 0, 1, 2, 3,… ta được 0, 7, 14, 21,…
Các bội của 7 là: 0, 7, 14, 21,…
Mà cần tìm các bội của 7 nhỏ hơn 20 nên các số thỏa mãn yêu cầu là 0, 7, 14.
Vậy các bội nhỏ hơn 20 của 7 là 0, 7, 14.
2.2 Cách tìm ước của một số
Để tìm các ước của số tự nhiên n lớn hơn 1 ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó, các phép chia hết cho ta số chia là ước của n.
Ví dụ: Tìm các ước của 15.
Lời giải:
Thực hiện phép chia số 15 cho lần lượt các số tự nhiên từ 1 đến 15. Các phép chia hết là: 15 : 1 = 15; 15 : 3 = 5; 15 : 5 = 3; 15 : 15 = 1.
Vì vậy, các ước của 15 là 1, 3, 5, 15.
II. Tính chất chia hết
1. Tính chất chia hết của một tổng
Tổng quát: Nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Cụ thể đối với tổng 2 số hạng:
Nếu 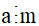 và
và 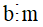 thì
thì 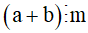 .
.
Khi đó ta có: (a + b) : m = a : m + b : m.
Ví dụ:
+ Ta có: 4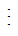 2 và 6
2 và 6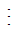 2 thì (6 + 4)
2 thì (6 + 4)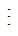 2.
2.
Khi đó: (4 + 6) : 2 = 4 : 2 + 6 : 2.
+ Ta có: 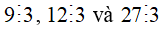 thì
thì 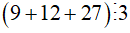 .
.
Khi đó: ( 9 + 12 + 27) : 3 = 9 : 3 + 12 : 3 + 27 : 3
2. Tính chất chia hết của một hiệu
Tổng quát: Nếu số bị trừ và số trừ đều chia hết cho cùng một số thì hiệu chia hết cho số đó.
Cụ thể:
Với a ≥ b :
Nếu 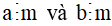 thì
thì 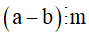 .
.
Khi đó ta có: (a – b) : m = a : m – b : m.
Ví dụ: Ta có: 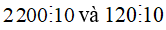 thì
thì 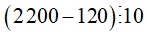 .
.
Khi đó: (2200 - 120) :10 =2200 : 10 -120:10 .
3. Tính chất chia hết của một tích
Tổng quát: Nếu một thừa số của tích chia hết cho một số thì tích chia hết cho số đó.
Cụ thể: Nếu 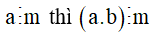 với mọi số tự nhiên b.
với mọi số tự nhiên b.
Ví dụ: Ta thấy 50 chia hết cho 5 nên tích 50 . 2016 chia hết cho 5.