Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Lũy thừa với số mũ tự nhiên, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Lũy thừa với số mũ tự nhiên. Mời các bạn đón xem:
Bài tập Toán 6 Lũy thừa với số mũ tự nhiên
A. Bài tập Lũy thừa với số mũ tự nhiên
Bài 1. Hoàn thành bảng sau:
|
Lũy thừa |
Cơ số |
Số mũ |
Giá trị của biểu thức |
|
52 |
|
|
|
|
|
6 |
3 |
|
|
25 |
|
|
|
|
|
10 |
|
1000 |
Lời giải
|
Lũy thừa |
Cơ số |
Số mũ |
Giá trị của biểu thức |
|
52 |
5 |
2 |
25 |
|
63 |
6 |
3 |
216 |
|
25 |
2 |
5 |
32 |
|
103 |
10 |
3 |
1000 |
Bài 2. Khối lượng của trái đất khoảng 6.1021 tấn. Khối lượng mặt trăng khoảng 7,4.1019 tấn. Hỏi khối lượng trái đất gấp bao nhiêu lần khối lượng mặt trăng.
Lời giải
Khối lượng trái đất gấp số lần khối lượng mặt trăng là:
6.1021 : (7,4.1019) = 600.1019:(7,4.1019) = (600:7,4) ≈ 81 (lần).
Khối lượng trái đất gấp 81 lần khối lượng mặt trăng.
Bài 3. Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa.
a) x . x8 ;
b) 42 . 64;
c) 10 . 2 . 5.
Hướng dẫn giải
a) x . x8 = x1 . x8 = x1 + 8 = x9 ;
b) 42 . 64 = 42 . 4 . 4 . 4 = 42 . 43 = 42 + 3 = 45 ;
c) 10 . 2 . 5 = 10 . (2 . 5) = 10 . 10 = 102.
Bài 4. Tính 44 . 4 : 16 + 6.
Hướng dẫn giải
44 . 4 : 16 + 6
= 44 . 41 : 42 + 6
= 44 + 1 – 2 + 6
= 43 + 6
= 4 . 4 . 4 + 6
= 64 + 6 = 70.
Bài 5. Tìm x biết: (2x + 1)3 = 729.
Hướng dẫn giải
(2x + 1)3 = 729
(2x + 1)3 = 93
(2x + 1) = 9
2x + 1 = 9
2x = 9 – 1
2x = 8
x = 4.
Vậy x = 4.
Bài 6. Thực hiện các phép tính:
a) 37 . 27 . 81;
b) 100 . 1 000 . 10 000;
c) 1254 : 58.
Lời giải:
a) Ta có: 37 . 27 . 81 = 37.(3.3.3).(3.3.3.3) = 37 . 33 . 34 = 37 + 3 + 4 = 314
b) Ta có: 100 . 1 000 . 10 000 = (102) . (103) . (104) = 102 + 3 + 4 = 109
c) Ta có:
1254 : 58 = (5.5.5)4 : 58 = (53)4 : 58 = [53.53.53.53] : 58
= 53 + 3 + 3 + 3 : 58 = 512 : 58 = 512 - 8 = 54.
Bài 7. So sánh
a) 22 . 23 và 26;
b) 32 và 23;
c) 52 và 5 . 2.
Lời giải:
a) Ta có: 22 . 23 = 22 + 3 = 25
Vì 5 < 6 nên 25 < 26
Vậy 22 . 23 < 26.
b) Ta có: 32 = 3 . 3 = 9; 23 = 2 . 2 . 2 = 8
Vì 8 < 9 nên 23 < 32 hay 32 > 23
Vậy 32 > 23.
c) Ta có: 52 = 5 . 5 = 25
5 . 2 = 10
Vì 25 > 10 nên 52 > 5 . 2
Vậy 52 > 5 . 2.
Câu 8. Chọn phát biểu đúng.
A. a3 còn được gọi là a lập phương.
B. a3 = a + a + a.
C. a3 = a.3.
D. Số mũ của a3 là a.
Lời giải
a3 còn được gọi là a lập phương. Do đó A đúng.
Ta có a3 = a.a.a. Do đó B, C sai.
Số mũ của a3 là 3. Do đó D sai.
Đáp án: A
Câu 9. Viết kết quả của phép tính sau dưới dạng một lũy thừa: 5.5.5.5?
A. 5.4.
B. 54.
C. 55.
D. 53..
Lời giải 5.5.5.5 = 54.
Đáp án: B
Câu 10. Ta có am:an = am – n với điều kiện là gì?
A. a ≠ 0;
B. a ≠ 0 và m < n.
C. a ≠ 0 và m > n.
D. a ≠ 0 và m ≥ n.
Lời giải am:an = am – n với a ≠ 0 và m ≥ n
Đáp án: D
Câu 11. Lập phương của 7 được viết như thế nào?
A. 72; B. 73; C. 7.3; D. 7.2.
Lời giải Lập phương của 7 là: 73.
Đáp án: B
Câu 12. 16 là lũy thừa của số tự nhiên nào, và có số mũ bằng bao nhiêu?
A. Lũy thừa của 2, số mũ bằng 4
B. Lũy thừa của 4, số mũ bằng 3
C. Lũy thừa của 2, số mũ bằng 3
D. Lũy thừa của 2, số mũ bằng 3
Lời giải
16 = 4.4 = 42. 16 là lũy thừa của số 4 và số mũ bằng 2.
16 = 2.2.2.2 = 22. 16 là lũy thừa của số 2 và số mũ bằng 4.
Đáp án: A
Câu 13. Lũy thừa bậc n của số tự nhiên a được viết là:
A. an;
B. a.n;
C. a + n;
D. a – n.
Lời giải Lũy thừa bậc n của số tự nhiên a được viết là: an.
Đáp án: A
Câu 14. Cách đọc 22 nào là sai?
A. hai mũ hai;
B. hai lũy thừa hai;
C. hai bình phương;
D. hai nhân hai.
Lời giải
Các cách đọc 22 là:
- Hai mũ hai;
- Hai bình phương;
- Hai lũy thừa hai.
Vậy D sai.
Đáp án: D
Câu 15. Lũy thừa nào dưới đây biểu diễn thương
A. 517
B. 175
C. 1711
D.176
Trả lời:
Ta có:
Đáp án cần chọn là: B
Câu 16. Chọn câu đúng
A.
B.
C.
D.
Trả lời:
+ Ta có: nên A sai
+ nên B đúng
+ nên C, D sai
Đáp án cần chọn là: B
Câu 317. Chọn câu sai
A.53 < 35
B. 34 > 25
C. 43 = 26
D. 43 > 82
Trả lời:
Ta có:
+ 53 = 5.5.5 = 125; 35 = 3.3.3.3.3 = 243 nên 53 < 35 (A đúng
+ 34 = 3.3.3.3 = 81 và 25 = 2.2.2.2.2 = 32 nên 34 > 25 (B đúng)
+ 43 = 4.4.4 = 64 và 26 = 2.2.2.2.2.2 = 64 nên 43 = 26 nên 43 = 26 (C đúng)
+ 43 = 64; 82 = 64 nên 43 = 82 (D sai
Đáp án cần chọn là: D
Câu 18. Tính 24 + 16 ta được kết quả dưới dạng lũy thừa là
A. 220
B. 24
C. 25
D. 210
Trả lời:
Ta có 24 + 16 = 2.2.2.2 + 16
= 16 + 16 =32 =2.2.2.2.2
= 25
Đáp án cần chọn là: C
Câu 19. Tìm số n thỏa mãn 4n = 43.45.
A. n = 15;
B. n = 8;
C. n = 7;
D. n = 2.
Lời giải
4n = 43.45
4n = 43 + 5
4n = 48
n = 8.
Đáp án: B
Câu 20. Tìm số tự nhiên x, biết: x2 = 16.
A. x = 4;
B. x = 2;
C. x = 8;
D. x = 16.
Lời giải
x2 = 16
x2 = 42
x = 4
Vậy x = 4.
Đáp án: A
Câu 21. Tính 23?
A. 6.
B. 8.
C. 12.
D. 16.
Lời giải Ta có 23 = 8.
Đáp án: B
B. Lý thuyết Lũy thừa với số mũ tự nhiên
I. Lũy thừa
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.
an = a . a ….. a (n thừa số a) (n )
Ta đọc an là “a mũ n” hoặc “lũy thừa bậc n của”.
Số a được gọi là cơ số, n được gọi là số mũ.
Ví dụ: 85 đọc là “tám mũ năm”, có cơ số là 8 và số mũ là 5.
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
Đặc biệt, a2 còn được đọc là “a bình phương” hay “bình phương của a”.
a3 được đọc là “a lập phương” hay “lập phương của a”.
Quy ước: a1 = a.
Ví dụ:
a) Tính 23 và 103.
b) Viết 10 000 000 dưới dạng lũy thừa của 10.
c) Viết 16 dưới dạng lũy thừa cơ số 4
Hướng dẫn giải
a) Số 23 là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:
23 = 2 . 2 . 2 = 8.
Số 103 là lũy thừa bậc 3 của 10 và là tích của 3 thừa số 10 nhân với nhau nên ta có:
103 = 10 . 10 . 10 = 1 000.
b) Số 10 000 000 được viết dưới dạng lũy thừa của 10 là:
10 000 000 = 10 . 10 . 10 . 10 . 10 . 10 . 10 = 107.
c) Số 16 được viết dưới dạng lũy thừa cơ số 4 là:
16 = 4 . 4 = 42.
II. Phép nâng lên lũy thừa
Lũy thừa bậc n của a, kí hiệu , là tích của n thừa số a:
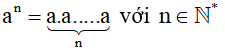
Trong đó:
a được gọi là cơ số
n được gọi là số mũ.
Quy ước: a1=a
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Chú ý:
+ an đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bậc n của a”.
+ a2 còn được gọi là “a bình phương” hay “bình phương của a”.
+ a3 còn được gọi là “a lập phương” hay “lập phương của a”.
Ví dụ:
7 . 7 . 7 . 7 = 74 (đọc là 7 mũ 4 hoặc là 7 lũy thừa 4, hoặc lũy thừa bậc bốn của 7)
16 = 2 . 2 . 2 . 2 = 24
Lưu ý: Với n là số tự nhiên khác 0, ta có: 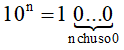
Ví dụ: 105 = 10 . 10 . 10 . 10 . 10 = 100 000
III. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
am . an = am + n
Ví dụ:
+) 23 . 24 = 23 + 4 = 27
+) a2 . a1 = a2 + 1 = a3
+) 42 . 45 = 42 + 5 = 47
IV. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
am : an = am - n (a # 0, m ≥ n)
Quy ước: a0 = 1 (a # 0) .
Ví dụ:
+ 97 : 93 = 97 - 3 = 94
+ 76 : 7 = 76 : 71 = 76 - 1 = 75
+ 33 : 33 = 33 - 3 = 30 = 1