Với giải sách bài tập Toán 6 Bài tập cuối chương 3 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài tập cuối chương 3
Lời giải:
Cách 1:
Diện tích của sân hình chữ nhật là: 12.9 = 108 (m2).
Tiền gạch bác An phải trả là: 108. 130 000 = 14 040 000 (đồng).
Tiền công thợ bác An phải trả là: 108.70 000 = 7 560 000 (đồng).
Tổng số tiền bác An phải trả là: 14 040 000 + 7 560 000 = 21 600 000 (đồng).
Vậy số tiền bác An phải trả là: 21 600 000 đồng.
Cách 2:
Diện tích của sân hình chữ nhật là: 12.9 = 108 (m2).
Tổng số tiền bác An phải trả là:
108. 130 000 + 108.70 000
= 108.(130 000 + 70 000)
=108. 200 000 = 21 600 000 (đồng).
Vậy số tiền bác An phải trả là: 21 600 000 đồng.
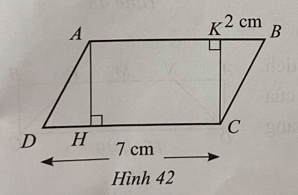
Lời giải:
Độ dài đường cao AH là: 28:7 = 4 (cm).
Độ dài cạnh AK bằng độ dài cạnh AB trừ đi độ dài cạnh BK và bằng: 7 – 2 = 5 (cm).
Diện tích hình chữ nhật AHCK là: 4.5 = 20 (cm2).
Vậy diện tích hình chữ nhật AHCK là 20 cm2.
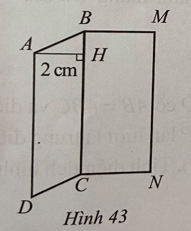
Lời giải:
Chiều rộng của hình chữ nhật BCNM là: (18:2):3 = 3 (cm).
Chiều dài của hình chữ nhật BCNM là: 2.3 = 6 (cm).
Diện tích hình chữ nhật BCNM là: 3.6 = 18 (cm2).
Diện tích hình bình hành ABCD với cạnh BC = 6cm và chiều cao tương ứng AH = 2cm là: 6.2 = 12 (cm2).
Diện tích Hình 43 bằng tổng diện tích hình bình hành ABCD là 12 cm2 và diện tích hình chữ nhật BCNM là 18 cm2 bằng: 12 + 18 = 30 (cm2).
Vậy diện tích hình 43 là 30 cm2.
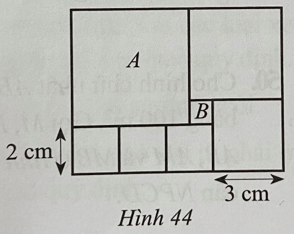
Lời giải:
Độ dài cạnh của hình vuông B là: 3 – 2 = 1 (cm).
Diện tích hình vuông B là: 1.1 = 1 (cm2).
Độ dài cạnh của hình vuông A là: 2.3 – 1 = 5 (cm).
Diện tích hình vuông A là: 5.5 = 25 (cm2).
Do đó diện tích hình vuông A gấp số lần diện tích hình vuông B là: 25:1 = 25 (lần).
Vậy diện tích hình vuông A gấp 25 lần diện tích hình vuông B.
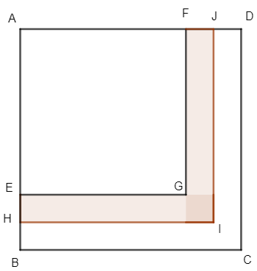
Lời giải:
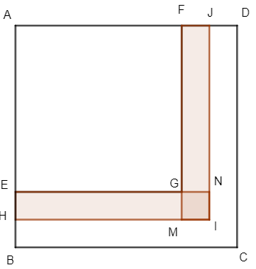
Đặt EG = a (cm), EH = b (cm).
Khi đó diện tích hình chữ nhật EGMH bằng hình chữ nhật GFJN bằng: a.b (cm2).
Diện tích hình vuông GNIM là: b.b = b2 (cm2).
Diện tích phần tô đậm bằng tổng diện tích hình chữ nhật EGMH, diện tích hình chữ nhật GFJN và diện tích hình vuông GNIM bằng: ab + ab + b2 = 2ab + b2 = 19 (cm2).
Vì 2ab là số tự nhiên chẵn nên b2 là số tự nhiên lẻ.
Hơn nữa b2 < 19 nên b2 = 1 hoặc b2 = 9 suy ra b = 1 hoặc b = 3.
Với b = 1 thì a = 9 cm, khi đó AB = 9 + 1.2 = 11 cm.
Diện tích hình vuông ABCD là: 11.11 = 121 cm2.
Với b = 3 thì 6a = 10, khi đó không có số tự nhiên a nào thỏa mãn nên loại.
Vậy diện tích hình vuông ABCD là 121 cm2.
a) Một hình chữ nhật.
b) Một hình bình hành.
So sánh diện tích của các hình ghép được.
Lời giải:
a) Cách ghép hai tam giác vuông thành hình chữ nhật như sau:
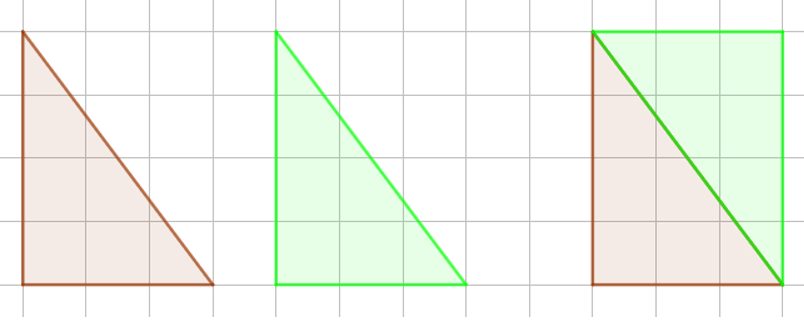
b) Cách ghép hai tam giác vuông thành hình bình hành như sau:
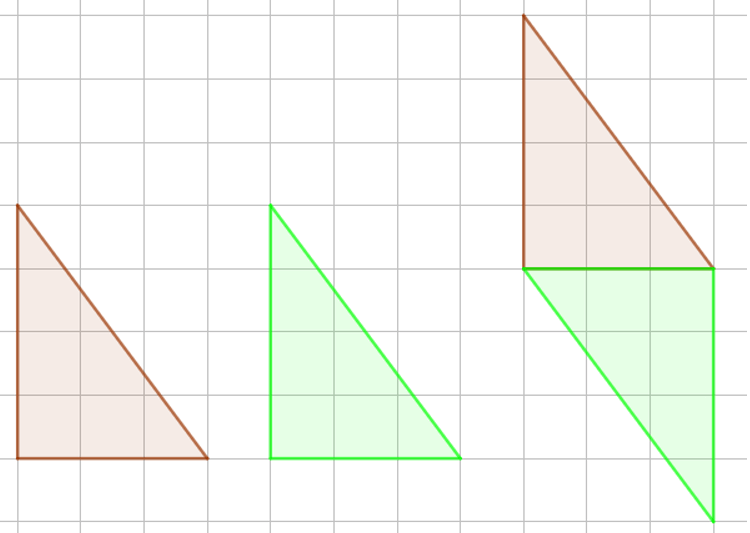
Diện tích của hình bình hành và hình chữ nhật trên bằng nhau vì cùng bằng diện tích của hai tam giác vuông cộng lại.
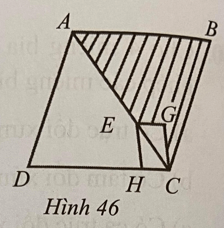
Lời giải:
Trong hình thoi ABCD, ta có: diện tích tam giác ABC bằng diện tích tam giác ADC.
Trong hình bình hành AEHD, ta có: diện tích tam giác EGC bằng diện tích tam giác EHC.
Diện tích phần gạch chéo bằng diện tích tam giác ABC trừ diện tích tam giác EGC.
Diện tích tứ giác AEHD bằng diện tích tam giác ADC trừ diện tích tam giác EHC.
Do đó diện tích phần gạch chéo bằng diện tích tứ giác AEHD.
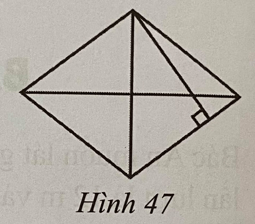
Lời giải:
Diện tích hình thoi là: 160.120:2 = 9 600 (cm2).
Vì tỉ số giữa chiều cao và độ dài cạnh hình thoi là 24:25 nên có thể coi chiều cao hình thoi là 24a và cạnh hình thoi là 25a.
Khi đó ta có diện tích hình thoi là: 25a.24a = 9 600 a2 = 16 a = 4 cm.
Chiều cao của hình thoi là: 24.4 = 96 (cm).
Vậy chiều cao của hình thoi là 96cm.
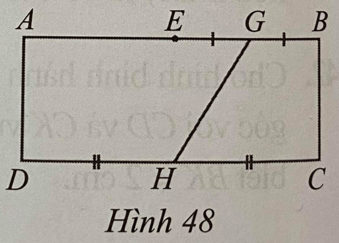
Lời giải:
Ta có hình thang GBCH và hình thang AGHD có cùng chiều cao. Do đó tỉ số diện tích của diện tích hình thang GBCH và diện tích hình thang AGHD bằng tỉ số tổng độ dài hai đáy của hình thang GBCH và tổng độ dài hai đáy của hình thang AGHD.
Đặt GB = GE = a suy ra CH = 2a, AB = 4a, AG = 3a.
Tổng độ dài hai đáy hình thang GBCH là: 2a + a = 3a.
Tổng độ dài hai đáy hình thang AGHD là: 2a + 3a = 5a.
Suy ra tỉ số tổng độ dài hai đáy của hình thang GBCH và tổng độ dài hai đáy của hình thang AGHD là 3:5.
Vậy tỉ số diện tích của diện tích hình thang GBCH và diện tích hình thang AGHD là 3:5.
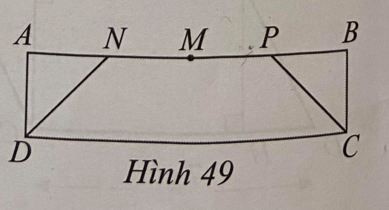
Lời giải:
Đặt BC = a (m) suy ra AB = 4a (m).
Diện tích hình chữ nhật ABCD là: a.4a = 4a2 (m2).
Mà diện tích hình chữ nhật ABCD bằng 100m2 nên 4a2 =100 a2 = 25 a = 5 m.
Suy ra BC = 5 m, AB = 20 m.
Khi đó NP = AB:2 = 20:2 = 10 m.
Ta có hình thang cân NPCD có chiều cao là BC = 5 m.
Diện tích hình thang cân NPCD là: (20 + 10).5:2 = 75 m2.
Vậy diện tích hình thang cân NPCD là 75 m2.
- Bạn Hùng nói: “Hình thoi chỉ có tâm đối xứng và không có trục đối xứng”.
- Bạn Kiên nói: “Hình chữ nhật không có tâm đối xứng và chỉ có trục đối xứng”.
- Bạn Minh phát biểu: “Hình vuông có cả tâm đối xứng và trục đối xứng”.
Theo em, bạn nào phát biểu đúng?
Lời giải:
Hình thoi là hình có tâm đối xứng là giao điểm của hai đường chéo và hai trục đối xứng là hai đường chéo. Do đó phát biểu của bạn Hùng là SAI.
Hình chữ nhật có tâm đối xứng là giao điểm của hai đường chéo và có hai trục đối xứng nối trung điểm của hai cạnh đối diện. Do đó phát biểu của bạn Kiên SAI.
Hình vuông có tâm đối xứng là giao điểm của hai đường chéo và có bốn trục đối xứng bao gồm hai đường chéo và hai đường nối trung điểm của hai cạnh đối diện. Do đó phát biểu của bạn Minh ĐÚNG.
Vậy phát biểu của bạn Minh là đúng.
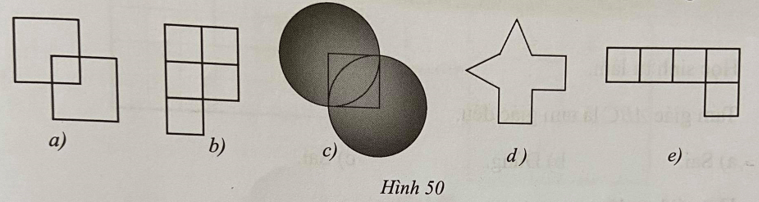
Lời giải:
Các hình không có trục đối xứng là Hình 50b), Hình 50e).
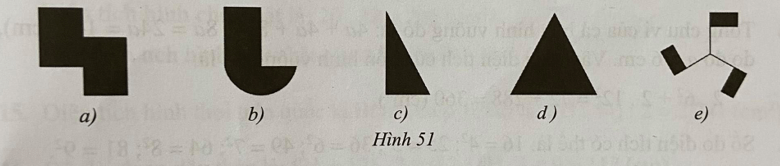
Lời giải:
Các hình có trục đối xứng là: Hình 51d).
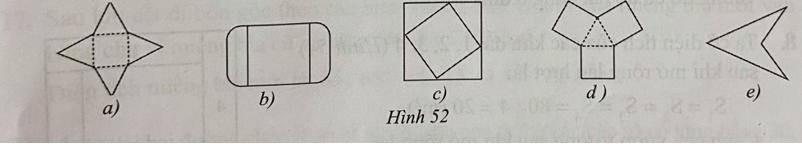
Lời giải:
Các hình có tâm đối xứng là: Hình 52a), Hình 52b), Hình 52c).
a) Biển báo cấm đi ngược chiều (Hình 53a): báo đường cấm các loại xe (cơ giới, thô sơ) đi vào theo chiều đặt biển, trừ các loại xe ưu tiên theo quy định.
b) Biển báo cấm dừng và đỗ xe (Hình 53b): biển có hiệu lực cấm các loại xe cơ giới dừng và đỗ ở phía đường có đặt biển, trừ các loại xe ưu tiên theo quy định.
c) Biển báo cấm sử dụng còi (Hình 53c): cấm các loại xe cơ giới sử dụng còi.
d) Biển báo cấm rẽ phải (Hình 53d): cấm các loại xe (cơ giới, thô sơ) rẽ phải ở những vị trí đường giao nhau trừ các loại xe ưu tiên theo quy định.
Lời giải:
Biển báo Hình 53c) và Hình 53d) không có tâm đối xứng.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
