Với giải bài tập Toán lớp 6 Bài tập cuối chương 3 chi tiết bám sát nội dung sgk Toán 6 Tập 1 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài tập cuối chương 3
Bài tập
Giải Toán 6 trang 117 Tập 1 Cánh diều
Bài 1 trang 117 Toán lớp 6 Tập 1: Tạo ra hình hộp có nắp
Hãy vẽ các hình chữ nhật trên một miếng bìa (mỏng) theo cách như ở Hình 96, sau đó cắt, gấp lại và dán mép để tạo ra hình hộp có nắp.
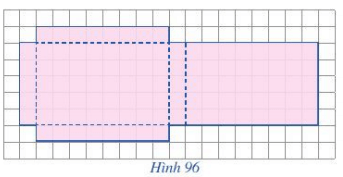
Lời giải:
- Chuẩn bị giấy mỏng có ô vuông, vẽ theo mẫu Hình 69
- Cắt phần đã vẽ theo một đường
- Cách gấp: gấp dựng đứng các hình chữ nhật nhỏ gắn với phần hình chữ nhật to thứ nhất, gấp phần hình chữ nhật thứ hai lên tạo thành nắp sau đó dán các mép gấp, ta được hình hộp có nắp.
Bài 2 trang 117 Toán lớp 6 Tập 1: Cho các hình sau đây:
(1) Đoạn thẳng AB.
(2) Tam giác đều ABC.
(3) Hình tròn tâm O.
(4) Hình thang cân ABCD (có đáy lớn CD)
(5) Hình thoi ABCD.
Trong các hình nói trên:
a) Hình nào có trục đối xứng? Chỉ ra trục đối xứng của hình đó.
b) Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó.
Lời giải:
a) Cả 5 hình đã cho đều có trục đối xứng như sau:
(1) Đoạn thẳng AB là hình có 1 trục đối xứng và trục đối xứng là đường thẳng d đi qua trung điểm O của đoạn thẳng AB và vuông góc với AB.
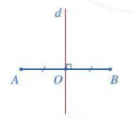
(2) Tam giác đều ABC là hình có trục đối xứng và có 3 trục đối xứng d1, d2, d3 như sau:
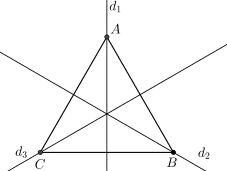
(3) Hình tròn tâm O có vô số trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm O của nó.
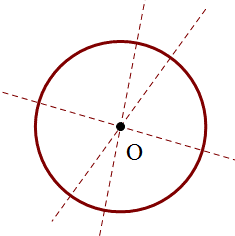
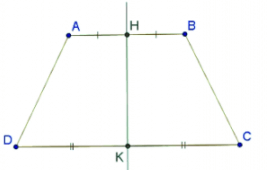
(4) Hình thang cân ABCD (có đáy lớn CD) là hình có 1 trục đối xứng và trục đối xứng là đường thẳng đi qua trung điểm H và K của 2 đáy AB và CD:
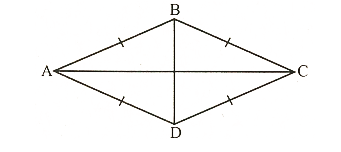
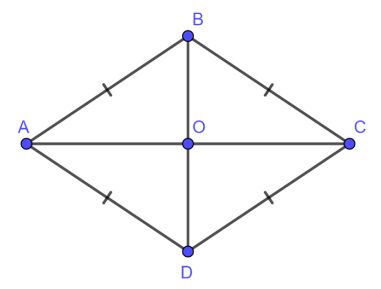
(5) Hình thoi ABCD có 2 trục đối xứng là hai đường chéo AC và BD
b) Trong 5 hình đã cho: đoạn thẳng AB, hình tròn tâm O, hình thoi ABCD là các hình có tâm đối xứng. Các hình tam giác đều ABC, hình thang cân ABCD là hình không có tâm đối xứng.
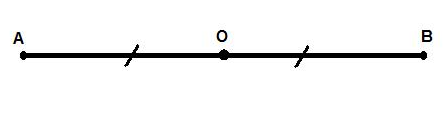
(1) Đoạn thẳng AB là hình có tâm đối xứng và tâm đối xứng là trung điểm O của AB
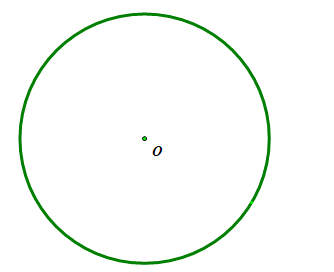
(3) Hình tròn tâm O có tâm đối xứng chính là tâm O
(5) Hình thoi ABCD có tâm đối xứng là giao điểm O của hai đường chéo AC và BD
Bài 3 trang 117 Toán lớp 6 Tập 1: Hãy quan sát xung quanh và chỉ ra những hình:
a) Có trục đối xứng.
b) Có tâm đối xứng
c) Vừa có trục đối xứng vừa có tâm đối xứng.
Lời giải:
a) Một số hình có trục đối xứng:
+) Hoa văn trang trí trên gạch hoa
+) Hình mặt cười
+) Hình con bướm
b) Một số hình có tâm đối xứng:
+) Hình biển báo giao thông
+) Hình chữ S
+) Hình chữ Z
c) Một số hình vừa có tâm đối xứng vừa có trục đối xứng
+) Hình trang trí bông hoa
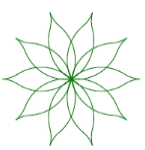
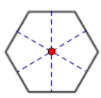
+) Lục giác đều
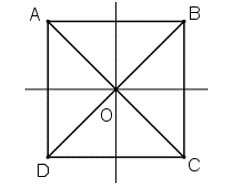
+) Hình vuông
Lời giải:
Một số ứng dụng của tính đối xứng trong thực tiễn:
+) Làm hình trang trí nghệ thuật
+) Thiết các các công trình kiến trúc
Nhà thờ Mosque (nhà thờ Hồi Giáo) tại Abu Dhabi.
Tháp Phước Duyên ở chùa Thiên Mụ (Huế)
Bài 5 trang 117 Toán lớp 6 Tập 1: a) Một hình thoi có cạnh 4 cm thì chu vi của nó bằng bao nhiêu?
b) Một hình vuông có chu vi là 40 cm thì cạnh của nó bằng bao nhiêu?
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7 cm thì chiều dài của nó bằng bao nhiêu?
d) Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì mỗi cạnh của nó bằng bao nhiêu?
Lời giải:
Để làm bài tập này, ta cần nhớ cách tính chu vi của các hình: hình thoi, hình vuông, hình chữ nhật (xem kiến thức ở các bài học).
a) Chu vi hình thoi có cạnh 4 cm là: 4 . 4 = 16 (cm)
b) Hình vuông có chu vi 40 cm thì có độ dài cạnh là: 40 : 4 = 10 (cm)
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7 cm.
Nửa chu vi của hình chữ nhật là: 30 : 2 = 15 (cm)
Chiều dài của hình chữ nhật là: 15 – 7 = 8 (cm)
d) Nửa chu vi hình chữ nhật là: 36 : 2 = 18 (cm)
Chiều dài gấp đôi chiều rộng, hay chiều rộng bằng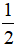 
chiều dài, khi đó ta có sơ đồ:
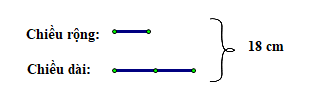
Tổng số phần bằng nhau là: 1 + 2 = 3 (phần)
Giá trị một phần hay chiều rộng là: 18 : 3 = 6 (cm)
Chiều dài là: 6 . 2 = 12 (cm)
Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là 12 cm và 6 cm.
Lời giải:
Em tự đo chiều dài và chiều rộng của các vật có dạng hình chữ nhật rồi áp dụng công thức tính chu vi hình chữ nhật để biết được chu vi các vật cần đo.
Giải Toán 6 trang 118 Tập 1 Cánh diều
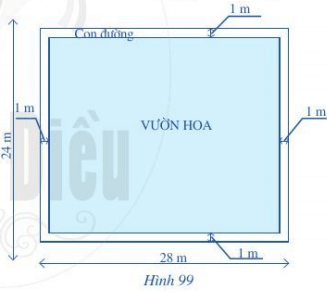
a) Tính diện tích mảnh đất có dạng hình chữ nhật đó.
b) Tính diện tích vườn hoa.
c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để lát đường đi. Cần dùng bao nhiêu viên gạch như thế? Biết rằng diện tích các mối nối và sự hao hụt là không đáng kể.
d) Người ta làm hàng rào xung quanh vườn hoa. Tính chiều dài hàng rào đó.
Lời giải:
a) Diện tích mảnh đất hình chữ nhật là:
28 . 24 = 672 (m2)
b) Quan sát hình 99, ta thấy sau khi bớt ra một phần đường đi thì phần vườn trồng hoa có dạng hình chữ nhật với:
Chiều dài phần vườn trồng hoa là: 28 – 1 – 1 = 26 (m)
Chiều rộng phần vườn trồng hoa là: 24 – 1 – 1 = 22 (m)
Diện tích phần vườn hoa là:
26 . 22 = 572 (m2)
c) Diện tích phần đường đi chính là hiệu diện tích mảnh đất với diện tích phần vườn hoa. Do đó diện tích phần đường đi là:
672 – 572 = 100 (m2)
Đổi 100 m2 = 1 000 000 cm2
Một viên gạch hình vuông có diện tích là:
50 . 50 = 2 500 (cm2)
Cần dùng số viên gạch là:
1 000 000 : 2 500 = 400 (viên gạch)
d) Phần chiều dài hàng rào xung quanh vườn hoa chính là chu vi phần vườn hoa có dạng hình chữ nhật
Vậy chiều dài hàng rào là: (22 + 26) . 2 = 96 m.
a) Tính diện tích mảnh đất có dạng hình chữ nhật đó.
b) Tính diện tích vườn hoa.
c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để lát đường đi. Cần dùng bao nhiêu viên gạch như thế? Biết rằng diện tích các mối nối và sự hao hụt là không đáng kể.
d) Người ta làm hàng rào xung quanh vườn hoa. Tính chiều dài hàng rào đó.
Lời giải:
a) Diện tích mảnh đất hình chữ nhật là:
28 . 24 = 672 (m2)
b) Quan sát hình 99, ta thấy sau khi bớt ra một phần đường đi thì phần vườn trồng hoa có dạng hình chữ nhật với:
Chiều dài phần vườn trồng hoa là: 28 – 1 – 1 = 26 (m)
Chiều rộng phần vườn trồng hoa là: 24 – 1 – 1 = 22 (m)
Diện tích phần vườn hoa là:
26 . 22 = 572 (m2)
c) Diện tích phần đường đi chính là hiệu diện tích mảnh đất với diện tích phần vườn hoa. Do đó diện tích phần đường đi là:
672 – 572 = 100 (m2)
Đổi 100 m2 = 1 000 000 cm2
Một viên gạch hình vuông có diện tích là:
50 . 50 = 2 500 (cm2)
Cần dùng số viên gạch là:
1 000 000 : 2 500 = 400 (viên gạch)
d) Phần chiều dài hàng rào xung quanh vườn hoa chính là chu vi phần vườn hoa có dạng hình chữ nhật
Vậy chiều dài hàng rào là: (22 + 26) . 2 = 96 m.
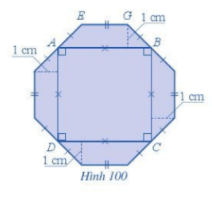
Lời giải:
Miếng bìa màu xanh như Hình 100 được tạo bởi 1 hình vuông ABCD có chu vi là 16 cm và 4 phần bìa bằng nhau có dạng hình thang cân như hình ABGE.
Độ dài cạnh của hình vuông ABCD là: 16 : 4 = 4 (cm)
Hay AB = 4 cm
Diện tích hình vuông ABCD là: 4 . 4 = 16 (cm2)
Diện tích phần còn lại (cả mảnh bìa trừ đi phần hình vuông ABCD) là:
28 – 16 = 12 (cm)
Diện tích phần còn lại của miếng bìa là tổng diện tích của 4 hình thang cân.
Do đó diện tích hình thang cân ABGE là: 12 : 4 = 3 (cm2)
Hình thang cân ABGE có diện tích 3 cm2 và có đáy AB = 4 cm, chiều cao 1 cm
Khi đó ta có: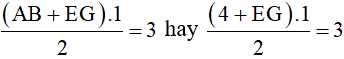 
Suy ra: EG = 3 . 2 : 1 – 4 = 2 (cm)
Vậy độ dài cạnh EG là 2 cm.
Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:
Bài 7: Đối xứng trong thực tiễn
Bài Thực hành phần mềm Geogebra
Bài 1: Thu thập, tổ chức, biểu diễn, phân tích và xử lí dữ liệu
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
