Với giải sách bài tập Toán 6 Bài 6: Hình có tâm đối xứng sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 6: Hình có tâm đối xứng

Bài 37 trang 116 sách bài tập Toán lớp 6 Tập 1: Các phát biểu sau đúng hay sai?

a) Tam giác đều ABC là hình đối xứng tâm.

b) Hình thang cân là hình có tâm đối xứng và giao điểm của hai đường chéo là tâm đối xứng.

c) Hình thoi ABCD có tâm đối xứng là điểm O (O là giao điểm của hai đường chéo AC và BD).

Lời giải:

Tam giác đều ABC là hình không có tâm đối xứng. Do đó phát biểu a) sai.

Hình thang cân là hình không có tâm đối xứng nên phát biểu b sai.

Hình thoi là hình có tâm đối xứng là giao điểm của hai đường chéo nên phát biểu c) đúng.

Bài 38 trang 116 sách bài tập Toán lớp 6 Tập 1: Trong Hình 39, các hình từ hình a) đến e), hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra tâm đối xứng của hình đó?

Lời giải:

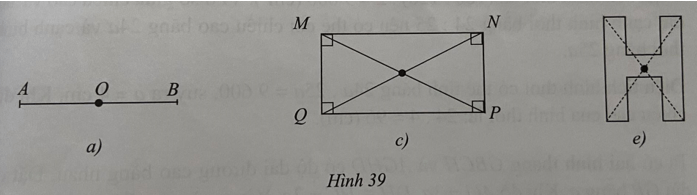
Trong các hình trên, hình có tâm đối xứng là:

Hình a) là hình có tâm đối xứng và tâm đối xứng là trung điểm O của AB.

Hình c) là hình có tâm đối xứng và tâm đối xứng là giao điểm của hai đường chéo MP và QN.

Hình e) là hình có tâm đối xứng như hình vẽ bên dưới:

Bài 39 trang 117 sách bài tập Toán lớp 6 Tập 1: Trong Hình 40, các hình từ a) đến e), họa tiết viên gạch hoa nào không có tâm đối xứng?

Lời giải:

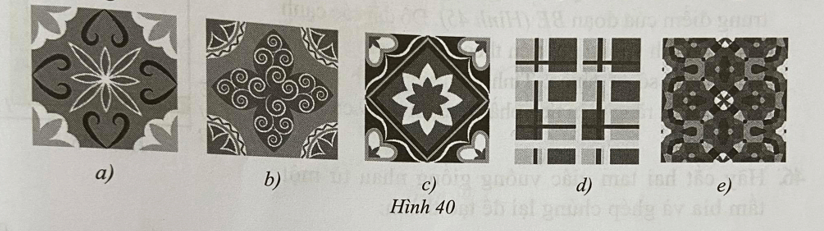
Hình không có tâm đối xứng là: Hình 40b) và Hình 40d).

Bài 40 trang 117 sách bài tập Toán lớp 6 Tập 1: Cho 4 miếng bìa giống nhau (Hình 41). Hãy ghép các miếng bìa đó để thành các hình:

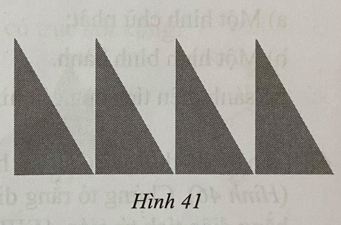
a) Có trục đối xứng;

b) Có tâm đối xứng;

c) Có cả trục và tâm đối xứng.

Lời giải:

a) Hình có trục đối xứng:

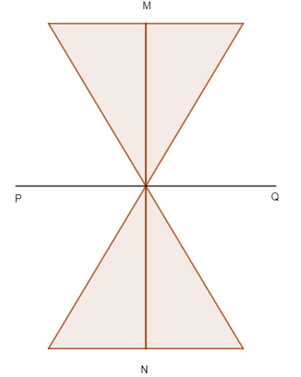
Hình này có hai trục đối xứng là MN và PQ.

b) Hình có tâm đối xứng

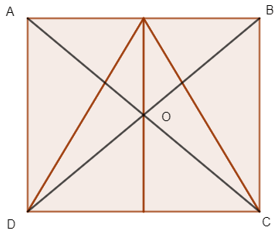
Tâm đối xứng của hình ABCD là giao điểm O của hai đường chéo AC và BD.

c) Hình có cả tâm và trục đối xứng:

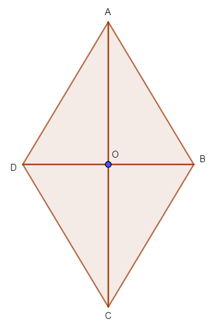
Trục đối xứng của hình là AC và BD.

Tâm đối xứng của hình là giao điểm O của hai đường chéo AC và BD.

Lý thuyết Hình có tâm đối xứng

I. Hình có tâm đối xứng

1. Cho đường tròn tâm O, đường kính AB.

+ Vì O là trung điểm của đoạn thẳng AB nên ta nói hai điểm A và B đối xứng với nhau qua tâm O.

+ Đường tròn tâm O là Hình có tâm đối xứng, tâm đối xứng chính là tâm O của đường tròn.

2. Lấy bốn chiếc ê ke giống nhau để xếp thành hình. Ta được một hình mới là Hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

Chú ý:Hình có tâm đối xứng còn được gọi là hình đối xứng tâm.

II. Tâm đối xứng của một số hình

1. Đoạn thẳng MN là Hình có tâm đối xứng và tâm đối xứng là trung điểm I của đoạn thẳng đó.

2. Hình tròn là Hình có tâm đối xứng và tâm đối xứng là tâm của nó.

3. Hình thoi, hình vuông, hình chữ nhật, hình lục giác đều có tâm đối xứng là giao điểm của các đường chéo.