Với giải sách bài tập Toán 6 Bài 4: Phép nhân, phép chia số tự nhiên sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 4: Phép nhân, phép chia số tự nhiên

Bài 23 trang 13 sách bài tập Toán lớp 6 Tập 1: Tính một cách hợp lí:

a) 17.88 + 17.12;

b) 25.32 + 4.92.25;

c) 3 119.121 - 3 119.11.11;

d) 24.(123 + 87) + (87 + 123).76.

Lời giải:

a) 17.88 + 17.12

= 17. (88 + 12)

= 17.100

= 1 700.

b) 25.32 + 4.92.25

= 25.(32 + 4.92)

= 25.(32 + 368)

= 25.400

= 10 000.

c) 3 119.121 - 3 119.11.11

= 3 119.121 - 3 119.121

= 3 119(121 – 121)

= 3 119.0

= 0.

d) 24.(123 + 87) + (87 + 123).76

= 24.210 + 210.76

= 210.(24 + 76)

= 210. 100

= 21 000.

Bài 24 trang 13 sách bài tập Toán lớp 6 Tập 1: Tính bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng và phép trừ (theo mẫu):

Mẫu: 106.21 = (100 + 6).21

= 100.21 + 6.21

= 2 100 + 6(20 +1)

= 2 100 + 6.20 + 6.1

= 2 100 + 120 + 6

= 2 226.

a) 35.29; b) 403.54; c) 9 998.12.

Lời giải:

a) 35.29

= (30 + 5).29

= 30.29 + 5.29

= 870 + 5.(20 + 9)

= 870 + 5.20 + 5.9

= 870 + 100 + 45

= 1 015.

b) 403.54

= (400 + 3).54

= 400.54 + 3.54

= 21 600 + 3.(50 + 4)

= 21 600 + 3.50 + 3.4

= 21 600 + 150 + 12

= 21 762.

c) 9 998.12

= (10 000 – 2).12

= 10 000.12 – 2.12

= 120 000 – 24

= 119 976.

Bài 25 trang 13 sách bài tập Toán lớp 6 Tập 1: So sánh tích 2 020.2 020 và tích 2 019.2 021 mà không tính cụ thể giá trị của chúng.

Lời giải:

Ta có 2 019.2 021

= 2 019.(2 020 + 1)

= 2 019.2 020 + 2 019.1

Ta lại có: 2 020.2 020

= 2 020(2 019 + 1)

= 2 020.2 019 + 2 020.1.

Vì 2 019 < 2 020 nên 2 019.2 020 + 2 019.1 < 2 020.2 019 + 2 020.1.

Vậy 2 019.2 020 < 2 020.2 020.

Bài 26 trang 14 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x, biết:

a) 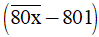.12 = 0;

b) 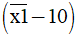.32 = 32;

c) x.x = 16;

d) 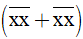.0 = 0.

Lời giải:

a) 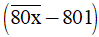.12 = 0

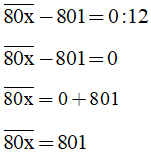
x = 1.

Vậy x =1.

b) 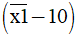.32 = 32

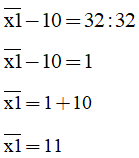
x = 1

Vậy x = 1.

c) x.x = 16

Ta thấy 4.4 = 16 nên x = 4.

Vậy x =4.

d) 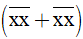.0 = 0

Ta thấy mọi số tự nhiên nhân với 0 đều bằng 0. 

Do đó có vô số 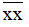 thỏa mãn điều kiện

Mà x là chữ số nên x ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9}.

Hơn nữa x ≠ 0 nên x ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9}.

Vậy x ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9}.

Bài 27 trang 14 sách bài tập Toán lớp 6 Tập 1: Nhờ tổ chức cuộc họp trực tuyến, công ty A đã giảm nhiều chi phí. Dưới đây là bảng các chi phí mà công ty A đã cắt giảm:

Chi phí	Số lượng	Đơn giá
Vé máy bay chặng Hà Nội – TP Hồ Chí Minh	9	1 209 000 đồng/vé
Vé máy bay chặng Hà Nội  - Đà Nẵng	5	538 000 đồng/vé
Hội trường	2	1 500 000 đồng/hội trường
In ấn tài liệu	60	18 000 đồng/tài liệu

Tổng chi phí công ty A đã cắt giảm là bao nhiêu?

Lời giải:

Tổng chi phí công ty A đã cắt giảm là:

1 209 000.9 + 538 000.5 + 1 500 000.2 + 18 000.60 = 17 651 000 (đồng).

Vậy tổng chi phí công ty A là 17 651 000 đồng.

Bài 28 trang 14 sách bài tập Toán lớp 6 Tập 1: Sử dụng giấy dán tường cho các mảng tường là xu thế đang được ưa chuộng. Ngày càng có nhiều loại giấy dán tường đẹp, mẫu mã sinh động, đa dạng và nhiều màu sắc. Sau đây là bảng báo giá giấy dán tường của một cửa hàng:

Giấy dán tường	Đơn giá theo cuộn (đồng/cuộn)	Đơn giá theo mét vuông (đồng/m2)
Nhóm giấy giá rẻ	920 000	90 000
Nhóm giấy giá trung bình	1 100 000	100 000
Nhóm giấy cao cấp	1 250 000	120 000

a) Nếu bác Lan mua 2 cuộn giấy dán tường giá rẻ và 25m² giấy dán tường giá trung bình thì theo bảng giá trên bác phải trả bao nhiêu tiền?

b) Do là khách quen nên của hàng giảm giá cho bác với mức giá giấy dán tường cao cấp như sau:

- Mua từ 1m² đến 20m² thì giá là 120 000 đồng/m².

- Mua từ 21m² đến 40m² thì giá là 115 000 đồng/m².

- Mua từ 41m² đến 60m² thì giá là 102 000 đồng/m².

- Mua nhiều hơn 60m² thì giá là 95 000 đồng/m².

Nếu bác Lan mua 1 cuộn giấy dán tường giá trung bình và 42 m² giấy dán tường cao cấp thì bác phải trả bao nhiêu tiền?

Lời giải:

a) Số tiền bác Lan mua 2 cuộn giấy dán tường giá rẻ là: 2.920 000 = 1 840 000 (đồng).

Số tiền bác Lan mua 25m² giấy dán tường giá trung bình là: 25.100 000 = 2 500 000 (đồng).

Vậy số tiền bác Lan mua 2 cuộn giấy dán tường giá rẻ và 25m² giấy dán tường giá trung bình: 1 840 000 + 2 500 000 = 4 340 000 (đồng).

b) Số tiền bác Lan phải trả cho 1 cuộn giấy dán tường giá trung bình là: 1 100 000 (đồng).

Số tiền bác Lan phải trả cho 42m² giấy dán tường cao cấp là: 42.102 000 = 4 284 000 (đồng).

Vậy tổng số tiền bác Lan phải trả cho 1 cuộn giấy dán tường giá trung bình và 42m² giấy dán tường cao cấp là:  1 100 000 + 4 284 000 = 5 384 000 (đồng).

Bài 29 trang 15 sách bài tập Toán lớp 6 Tập 1: Bình Ngô đại cáo ra đời vào năm nào?

Năm 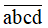 Nguyễn Trãi viết Bình Ngô đại cáo tổng kết thắng lợi của cuộc kháng chiến do Lê Lợi lãnh đạo chống quân Minh. Biết rằng  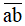gấp đôi số ngày trong một tuần lễ, còn  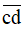gấp đôi của 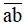. Tính xem năm đó là năm nào.

Lời giải:

Số ngày trong một tuần lễ là 7 ngày thì gấp đôi số ngày trong một tuần lễ là 14.

Suy ra 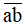 = 14.

Gấp đôi 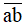 là 14.2 = 28.

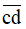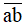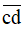Vì  gấp đôi của  nên  = 28.

Vậy năm đó là năm 1428.

Bài 30 trang 15 sách bài tập Toán lớp 6 Tập 1:

a) Tích các số tự nhiên từ 16 đến 57 có chữ số tận cùng là chữ số nào?

b) Tích tất cả các số tự nhiên lẻ có ba chữ số có chữ số tận cùng là chữ số nào?

Lời giải:

a) Các số tự nhiên từ 16 đến 57 có chứa số 50, mà bất kì một số nào nhân với số tròn chục đều cho kết quả là một số có chữ số tận cùng là 0 nên là tích của các số này sẽ có chữ số tận cùng là 0.

b) Các số tự nhiên lẻ có ba chữ số thì có chứa số có chữ số tận cùng là 5, mà bất kì số nào nhân với số có tận cùng là 5 đều cho kết quả có tận cùng là 5 nên tích của các chữ số này có tận cùng là 5.

Bài 31 trang 15 sách bài tập Toán lớp 6 Tập 1: Đặt tính rồi tính:

a) 5 292:12;

b) 534 127:11;

c) 9 564:123;

d) 209 943:321.

Lời giải:

a)

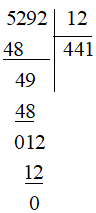
Vậy 5 292:12 = 441.

b) 

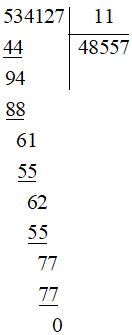
Vậy 534 127:11 = 48 557.

c) 

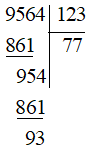
Vậy 9 564:123 = 77 (dư 93).

d) 

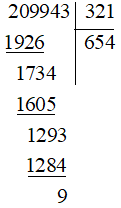
Vậy 209 943:321 = 654 (dư 9).

Bài 32 trang 15 sách bài tập Toán lớp 6 Tập 1: Một thư viện cần xếp 5 628 quyển sách vào các giá sách. Mỗi giá sách có 11 ngăn, mỗi ngăn xếp 32 quyển sách. Cần ít nhất bao nhiêu giá sách để xếp hết số sách trên?

Lời giải:

Một giá sách có thể xếp được số quyển sách là: 11.32 = 352 (quyển sách).

Ta có: 5 628:352 = 15 (dư 348) nên xếp đủ vào 15 giá sách thì còn thừa 348 quyển sách chưa được xếp. Do đó phải dùng thêm một giá sách nữa để xếp 348 quyển sách trên.

Vậy cần ít nhất: 15 + 1 = 16 (giá sách).

Bài 33 trang 15 sách bài tập Toán lớp 6 Tập 1: Có 1 000 cán bộ công nhân viên trên địa bàn thành phố Hà Nội đã tham gia ngày “Toàn dân hiến máu tình nguyện 7/4”. Mỗi người hiến tặng 450ml máu của mình. Với số máu được hiến tặng trên sẽ cấp cứu được cho bao nhiêu bệnh nhân, biết rằng trung bình mỗi bệnh nhân cần 1 500ml máu?

Lời giải:

Số máu các cán bộ công nhân viên trên địa bàn thành phố Hà Nội đã hiến được là:

1 000.450 = 450 000 (ml)

Ta có: 450 000:1 500 = 300 nên với số máu được hiến tặng này sẽ cấp cứu được cho 300 bệnh nhân.

Bài 34 trang 15 sách bài tập Toán lớp 6 Tập 1: Bạn Tú cần mua hai đôi giày thể thao có giá niêm yết là 810 000 đồng và 1 290 000 đồng. Cửa hàng A giảm nửa giá các loại giày trên. Cửa hàng B khuyến mãi các giày đó: nếu mua một đôi giày thì tặng một đôi giày tùy chọn (giá không hơn đôi đã mua). Bạn Tú nên mua giày ở cửa hàng nào thì có giá rẻ hơn?

Lời giải:

Nếu mua ở cửa hàng A thì bạn Tú sẽ phải trả số tiền là:

(810 000 + 1 290 000):2 = 2 100 000:2 = 1 050 000(đồng).

Nếu mua ở cửa hàng B thì bạn Tú sẽ mua đôi 1 290 000 đồng và được tặng đôi 810 000 đồng. Do đó số tiền phải trả là: 1 290 000 đồng.

Vậy bạn Tú nên mua giày ở cửa hàng A thì có giá rẻ hơn.

Bài 35 trang 15 sách bài tập Toán lớp 6 Tập 1: Bạn Hoa đã thực hiện phép chia hai số tự nhiên có số chia bằng 27 và được kết quả có số dư lớn hơn 24 và tổng của số bị chia và thương bằng 361. Tìm số bị chia và thương của phép chia mà bạn Hoa đã thực hiện.

Lời giải:

Gọi số bị chia là a, thương là q và số dư là r.

Ta có: a = q.27 + r (24 < r < 27).

Vì tổng của số bị chia và thương bằng 361 nên ta có: a + q = 361(*).

Thay a = q.27 + r vào biểu thức (*), ta được:

q.27 + r + q = 361

28q + r = 361

r = 361 – 28q.

Mà 24 < r < 27 nên 24 < 361 – 28q < 27 hay 334 < 28q < 337

Suy ra

TH1: 28q = 335

q = 335:28

q = 11(dư 27)

TH2: 28q = 336

q = 336:28

q = 12.

Khi đó a = 349.

Vậy số bị chia là 349 và thương là 12.

Bài 36 trang 15 sách bài tập Toán lớp 6 Tập 1: Bạn Chi đố bạn Đức xòe bàn tay ra và đếm các ngón tay như sau: Bắt đầu đếm từ ngón cái đến ngón út với các số 1; 2; 3; 4; 5; quay lại từ ngón áp út đến ngón cái với các số 6; 7; 8; 9; đếm tiếp từ ngón trỏ đến ngón áp út với các số 10; 11; 12; 13 (Hình 3). Nếu bạn Đức cứ đếm như vậy thì số 85 sẽ rơi vào ngón tay nào?

Lời giải:

Ta nhận thấy có ngón cái, ngón giữa và ngón út là các ngón bao gồm các dãy số lẻ.

Ngón trỏ và ngón áp út là các ngón gồm các dãy số chẵn.

Ngón cái bao gồm các số 1; 9; 17; 25; …

Các số này chia cho 8 dư 1 mà số 81 chia 8 cũng dư 1 nên số 81 sẽ rơi vào ngón cái.

Như vậy ngón trỏ là số 82, ngón giữa là 83, ngón áp út là 84 và ngón út là 85.

Vậy số 85 sẽ rơi vào ngón út.

Lý thuyết Phép nhân và phép chia các số tự nhiên

I. Phép nhân 

1. Phép nhân hai số tự nhiên

a x b = c 

(thừa số) x (thừa số) = (tích)

Ví dụ: 5 x 2 = 10; 20 x 3 = 60 

Quy ước: 

+ Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.” 

Ví dụ: 5 x 2 = 5 . 2 

+ Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số

Ví dụ: a x b = a . b = ab hoặc 4. a . b = 4ab

+ Khi nhân hai số có nhiều chữ số, thông thường đặt tính rồi tính, chú ý khi viết các tích riêng (tích riêng thứ hai lùi sang bên trái một cột so với tích riêng thứ nhất, tích riêng thứ ba lùi sang bên trái hai cột so với tích riêng thứ nhất,…)
Ví dụ: Đặt tính rồi tính: 341 x 157

         

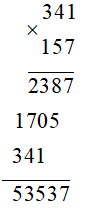
Vậy 341 x 157 = 53 537.

2. Tính chất của phép nhân

Phép nhân các số tự nhiên có các tính chất sau:

+ Giao hoán:               a . b = b . a

+ Kết hợp:                  (a . b) . c = a . (b . c)

+ Nhân với số 1:         a . a = 1 . a = a

+ Phân phối đối với phép cộng và phép trừ:

a . (b + c) = a. b + a . c

a . (b – c) = a . b – a . c

Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a. b. c có thể được tính theo một trong hai cách sau:

a . b. c = (a . b) . c hoặc a . b . c = a . (b . c)

Ví dụ: Tính một cách hợp lý: 

a) 20 . 36 . 5 

b) 34 . 28 + 34 . 72 

Lời giải:

a) 20 . 36 . 5 

= 20 . 5 . 36           (tính chất giao hoán)

= (20 . 5) . 36         (tính chất kết hợp)

= 100 . 36 

= 3 600 

b) 34 . 28 + 34 . 72 

= 34 . (28 + 72) 

= 34 . 100 

= 3 400 

II. Phép chia

1. Phép chia hết 

a : b = q       (b#0) 

(số bị chia) : (số chia) = (thương)

Ví dụ: 10 : 2 = 5; 30 : 5 = 6

Chú ý: 

+ Nếu a : b = q thì q = bq

+ Nếu a : b = q và q  0 thì a : q = b 

+ Thông thường, ta đặt tính chia để thực hiện phép chia.

Ví dụ: Đặt tính để tính thương: 139 004 : 236.

Lời giải: 

Ta có: 

    

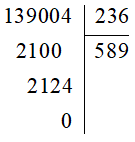
Vậy 139 004 : 236 = 589. 

2. Phép chia có dư

Cho hai số tự nhiên a và b với  . Khi đó luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó  .

Chú ý: 

+ Khi r = 0 ta có phép chia hết.

+ Khi r # 0  ta có phép chia có dư. Ta nói: a chia cho b được thương là q và số dư là r.

Kí hiệu: a : b = q (dư r)

Ví dụ: Đặt tính để tính thương và số dư của phép chia: 

5 125 : 320.

Lời giải: 

Ta có: 

 

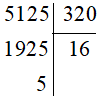
Vậy 5 125 : 320 = 16 (dư 5).