Với giải sách bài tập Toán 6 Bài 1: Tập hợp sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 1: Tập hợp
Bài 1 trang 6 sách bài tập Toán lớp 6 Tập 1: Liệt kê các phần tử của mỗi tập hợp sau:
a) A là tập hợp các ngày trong tuần;
b) B là tập hợp các chữ cái xuất hiện trong từ “HAM HỌC”.
c) C là tập hợp các chữ số xuất hiện trong số 303 530.
Lời giải:
a) Các ngày trong tuần bao gồm: thứ hai, thứ ba, thứ tư, thứ năm, thứ sáu, thứ bảy và chủ nhật.
Vậy A = {thứ hai; thứ ba; thứ tư; thứ năm; thứ sáu; thứ bảy; chủ nhật}.
b) Các chữ cái xuất hiện trong từ “HAM HỌC” là: H, A, M, H, O, C.
Vì các phần tử trong tập hợp chỉ được liệt kê 1 lần nên B = {H; A; M; O; C}.
Vậy B = {H; A; M; O; C}.
c) Các chữ số xuất hiện trong số 303 530 là: 3; 0; 3; 5; 3; 0.
Vì các phần tử trong tập hợp chỉ được liệt kê 1 lần nên C = {3; 0; 5}.
Vậy C = {3; 0; 5}.
a) 2 
A b) 3 
A c) x 
A d) p 
A
e) 3 
B f) 1 
B g) m 
B h) y 
B
Lời giải:
a) 2 thuộc tập hợp A, ta viết 2 
A
b) 3 không thuộc tập hợp A, ta viết 3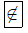 
A
c) x thuộc tập hợp A, ta viết x 
A
d) p không thuộc tập hợp A, ta viết p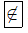 
A
e) 3 thuộc tập hợp B, ta viết 3 
B
f) 1 không thuộc tập hợp B, ta viết 1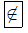 
B
g) m thuộc tập hợp B, ta viết m 
B
h) y không thuộc tập hợp B, ta viết y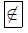 
B
Lời giải:
Các năng lượng tái tạo trên thế giới: năng lượng gió; năng lượng Mặt trời, năng lượng địa nhiệt.
Khi đó tập X = {năng lượng gió; năng lượng Mặt trời; năng lượng địa nhiệt}.
Các năng lượng tái tạo mà Việt Nam sản xuất: năng lượng gió; năng lượng Mặt trời.
Khi đó tập Y = {năng lượng gió; năng lượng Mặt trời}.
Tìm hiểu thêm về các biển báo giao thông trên, rồi viết tập hợp A gồm các loại phương tiện được phép lưu thông và tập hợp B gồm các loại phương tiện không được phép lưu thông trên đoạn đường đó dưới dạng liệt kê các phần tử.
Lời giải:
Hình 1 - a) Biển cấm xe đạp.
Hình 1 - b) Biển báo đường dành cho ô tô.
Hình 1 - c) Biển báo đường dành cho xe máy.
Các loại phương tiện được phép lưu thông trên đoạn đường này là: xe ô tô, xe máy.
Khi đó, A = {xe ô tô; xe máy}.
Các loại phương tiện không được phép lưu thông trên đoạn đường này là xe đạp.
Khi đó, B = {xe đạp}.
a) A = {x | x là số tự nhiên chẵn, 20 < x < 35};
b) B = {x | x là số tự nhiên lẻ, 150 < x < 160}.
Lời giải:
a) Các số tự nhiên chẵn thỏa mãn 20 < x < 35 là: 22; 24; 26; 28; 30; 32; 34.
Vậy bằng cách liệt kê A = {22; 24; 26; 28; 30; 32; 34}.
b) Các số tự nhiên lẻ thỏa mãn 150 < x < 160 là: 151; 153; 155; 157; 159.
Vậy bằng cách liệt kê A = {151; 153; 155; 157; 159}.
a) C = {x|x là số tự nhiên, x + 3 = 10}.
b) D = {x|x là số tự nhiên, x – 12 = 23}.
c) E = {x|x là số tự nhiên, x:16 = 0}.
d) G = {x|x là số tự nhiên, 0:x = 0}.
Lời giải:
a) Ta có x + 3 = 10
x = 10 – 3
x = 7.
Vậy C = {7}.
b) Ta có x – 12 = 23
x = 23 + 12
x = 35.
Vậy D = {35}.
c) Ta có: x:16 = 0
x = 0.16
x = 0.
Vậy E = {0}.
d) Ta có: 0:x = 0 nên x phải khác 0.
Do đó x là các số tự nhiên khác 0.
Vậy x ∈ {1; 2; 3; 4; 5; …}.
a) A = {13; 15; 17; …; 29};
b) B = {22; 24; 26; …; 42};
c) C = {7; 11; 15; 19; 23; 27};
d) D = {4; 9; 16; 25; 36; 49}.
Lời giải:
a) Ta nhận thấy các phần tử của tập hợp A là các số tự nhiên lẻ lớn hơn 12 và nhỏ hơn 30.
Theo cách chỉ ra tính chất đặc trưng, ta viết:
A = {x | x là số tự nhiên lẻ, 12 < x < 30}.
b) Ta nhận thấy các phần tử của tập hợp B là các số tự nhiên chẵn lớn hơn hoặc bằng 22 và nhỏ hơn hoặc bằng 42.
Theo cách chỉ ra tính chất đặc trưng, ta viết:
B = {x|x là số tự nhiên chẵn, 22 ≤ x ≤ 42}.
c)
+) Cách 1:
Ta có:
7 = 4.1 + 3; 11 = 4.2 + 3; 15 = 4.3 + 3; 19 = 4.4 + 3; 23 = 4.5 + 3; 27 = 4.6 + 3.
Ta nhận thấy các số trên đều có dạng 4.x + 3 với x ∈ {1,2,3,4,5,6} .
Theo cách chỉ ra tính chất đặc trưng, ta viết:
C = {4x + 3| x là số tự nhiên, 0 < x < 7}.
+) Cách 2:
Ta nhận thấy các phần tử trong tập hợp C là các số tự nhiên lẻ và cách nhau 4 đơn vị.
C = {xk| xk là số tự nhiên lẻ, xk+1 – xk = 4,k ∈ N }.
d) Ta thấy các phần tử của tập hợp D là các số chính phương lớn hơn 3 và nhỏ hơn 50.
Theo cách chỉ ra tính chất đặc trưng, ta viết:
D = {x| x là số chính phương, 3 < x < 50}.
Lời giải:
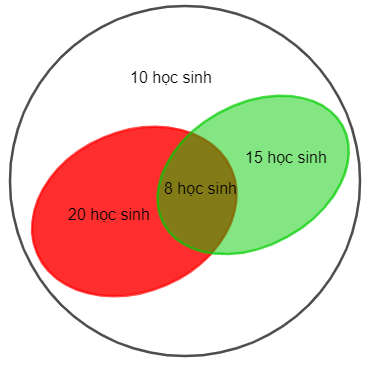
Số học sinh yêu thích riêng môn Ngữ văn là: 15 – 8 = 7 (học sinh).
Số học sinh yêu thích riêng môn Toán là: 20 – 8 = 12 (học sinh).
Tổng số học sinh yêu thích môn Ngữ văn và Toán là: 12 + 7 + 8 = 27 (học sinh).
Số học sinh của lớp 6A là: 27 + 10 = 37 (học sinh).
Lý thuyết Tập hợp
1. Tập hợp
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
Ví dụ:
+ Tập hợp các đồ vật (sách, bút) đặt trên bàn.
+ Tập hợp học sinh lớp 6A.
+ Tập hợp các số tự nhiên nhỏ hơn 7.
+ Tập hợp các số trên mặt đồng hồ trong hình dưới
2. Kí hiệu và cách viết tập hợp
Tên tập hợp được viết bằng chữ cái in hoa như: A, B, C,…
Ví dụ:
+ Tập hợp A gồm các số tự nhiên nhỏ hơn 5
Ta viết: A = {0; 1; 2; 3; 4}
Các số 0; 1; 2; 3; 4 được gọi là các phần tử của tập hợp A.
+ Tập hợp B = {bóng rổ; bóng đá; cầu lông; bóng bàn}
Các phần của tập hợp B là: bóng rổ, bóng đá, cầu lông, bóng bàn.
Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
Chẳng hạn, với tập A ở trên, ta có thể viết như sau:
A = {2; 3; 1; 4; 0}
3. Phần tử thuộc tập hợp
Kí hiệu: ∈ (thuộc) và ∉ (không thuộc)
Ví dụ: Cho tập hợp B = {2; 3; 5; 6}
- Các số 2; 3; 5; 6 là các phần tử của tập hợp B, ta nói
+ Phần tử 2 (số 2) thuộc tập hợp B, viết là 2 ∈ B
+ Phần tử 3 (số 3) thuộc tập hợp B, viết là 3 ∈ B
+ Phần tử 5 (số 5) thuộc tập hợp B, viết là 5 ∈ B
+ Phần tử 6 (số 6) thuộc tập hợp B, viết là 6 ∈ B
- Ta thấy số 4 không là phần tử của tập hợp B, ta viết 4 ∉ B, đọc là 4 không thuộc B.
4. Cách cho tập hợp
Có hai cách cho một tập hợp
4.1 Liệt kê các phần tử của tập hợp.
Ví dụ: Quan sát các số được cho ở hình dưới:
Gọi A là tập hợp các số đó.
Các phần tử của tập hợp A là: 0; 1; 2; 3; 4
Ta viết: A ={0; 1; 2; 3; 4} .
4.2 Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ví dụ:Các phần tử của tập hợp A ở trên đều là các số tự nhiên nhỏ hơn 5. Ta có thể viết:
A = {x| x là số tự nhiên nhỏ hơn 5}.
4.3 Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
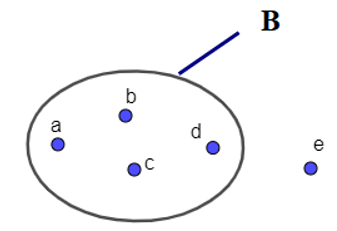
• Ngoài ra ta còn minh họa tập hợp bằng một vòng tròn kín, mỗi phần tử của tập hợp được biểu diễn bằng 1 dấu chấm bên trong vòng tròn kín đó, còn phần tử không thuộc tập hợp được biểu diễn bởi một dấu chấm bên ngoài vòng kín. Cách minh họa tập hợp như trên gọi là biểu đồ Ven (Venn).
Ví dụ: Tập hợp B trong hình vẽ là B = {a; b; c; d}; e ∉ B
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
:
