Với giải bài tập Toán lớp 6 Bài 1: Tập hợp chi tiết bám sát nội dung sgk Toán 6 Tập 1 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 1: Tập hợp
Video giải Toán 6 Bài 1: Tập hợp - Cánh diều
Trả lời câu hỏi giữa bài
Giải Toán 6 trang 6 Tập 1 Cánh diều
Luyện tập 1 trang 6 Toán lớp 6 Tập 1: Viết tập hợp A gồm các số tự nhiên lẻ nhỏ hơn 10.
Lời giải:
Các số tự nhiên lẻ nhỏ hơn 10 là: 1; 3; 5; 7; 9.
Do đó ta viết tập hợp A là:
A = {1; 3; 5; 7; 9}.
Lời giải:
Vì B = {2; 3; 5; 7} nên ta thấy tập hợp B gồm các phần tử là 2; 3; 5; 7.
Số 2 là một phần tử của tập hợp B. Ta viết 2 ∈ B, đọc là 2 thuộc B.
Số 4 không là phần tử của tập hợp B. Ta viết 4 ∉ B, đọc là 4 không thuộc B.
a) Tháng 2 
H;
b) Tháng 4 H;
c) Tháng 12 H.
Lời giải:
Ta đã biết các tháng dương lịch có 30 ngày là các tháng: tháng 4; tháng 6; tháng 9; tháng 11.
Do đó ta viết tập hợp H:
H = {tháng 4; tháng 6; tháng 9; tháng 11}.
a) Ta thấy tháng 2 không thuộc tập hợp H, ta viết:
Tháng 2 
H.
b) Ta thấy tháng 4 thuộc tập hợp H, ta viết:
Tháng 4 
H.
c) Ta thấy tháng 12 không thuộc tập hợp H, ta viết:
Tháng 12 H.
Gọi A là tập hợp các số đó.
a) Lệt kê các phần tử của tập hợp A và viết tập hợp A.
b) Các phần tử của tập hợp A có tính chất chung nào?
Lời giải:
a) Các phần tử của tập hợp A là 0; 2; 4; 6; 8. Ta viết: A = {0; 2; 4; 6; 8}.
b) Các phần tử của tập hợp A đều là các số tự nhiên chẵn nhỏ hơn 10. Ta có thể viết:
A = {x | x là số tự nhiên chẵn, x < 10}.
Giải Toán 6 trang 7 Tập 1 Cánh diều
Ta có: C = {x | x là số tự nhiên chia cho 3 dư 1, 3 < x < 18}
Vì 3 < x < 18 nên x là các số tự nhiên lớn hơn 3 và nhỏ hơn 18.
Lại có các số tự nhiên lớn hơn 3 và nhỏ hơn 18 là: 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17.
Mặt khác x lại là số tự nhiên chia cho 3 dư 1 thỏa mãn lớn hơn 3 và nhỏ hơn 18 nên các số tự nhiên x thỏa mãn yêu cầu là: 4; 7; 10; 13; 16.
Do đó ta viết tập hợp C dưới dạng liệt kê các phần tử như sau:
C = {4; 7; 10; 13; 16}.
Trong số 2 020, ta thấy có các chữ số là 2 và 0, trong đó mỗi chữ số được viết 2 lần. Mà ta đã biết, trong tập hợp mỗi phần tử được liệt kê một lần (nội dung kiến thức Trang 5/SGK).
Gọi N là tập hợp các chữ số xuất hiện trong số 2 020.
Do đó ta viết tập hợp N là:
N = {0; 2}.
Bài tập
a) A là tập hợp tên các hình trong Hình 3;
b) B là tập hợp các chữ cái xuất hiện trong từ “NHA TRANG”;
c) C là tập hợp tên các tháng của Quý II (biết một năm gồm bốn quý);
d) D là tập hợp tên các nốt nhạc có trong khuông nhạc ở Hình 4.
Lời giải:
a) Quan sát Hình 3, ta thấy các hình (ta đã được học ở Tiểu học) theo thứ tự từ trái qua phải là: hình chữ nhật; hình vuông; hình bình hành; hình tam giác; hình thang.
Do đó ta viết tập hợp A là:
A = {hình chữ nhật; hình vuông; hình bình hành; hình tam giác; hình thang}.
b) Ta thấy các chữ cái xuất hiện trong từ "NHA TRANG" là: N; H; A; T; R; A; N; G, trong đó các chữ cái N; A xuất hiện hai lần. Mà ta đã biết, trong tập hợp mỗi phần tử được liệt kê một lần (nội dung kiến thức Trang 5/SGK).
Do đó ta viết tập hợp B là:
B = {N; H; A; T; R; G}.
c) Ta đã biết một năm gồm bốn quý, mỗi quý gồm ba tháng liên tiếp nhau (tính từ tháng đầu tiên của năm) như sau:
Quý I: tháng 1; tháng 2; tháng 3
Quý II: tháng 4; tháng 5; tháng 6
Quý III: tháng 7; tháng 8; tháng 9
Quý IV: tháng 10; tháng 11; tháng 12
Do đó, ta viết tập hợp C gồm tên các tháng của Quý II là:
C = {tháng 4; tháng 5; tháng 6}.
d) Quan sát Hình 4, ta thấy tên các nốt nhạc theo thứ tự từ trái qua phải lần lượt là: Đồ; Rê; Mi; Pha; Son; La; Si.
Do đó ta viết tập hợp D như sau:
D = {Đồ; Rê; Mi; Pha; Son; La; Si}.
Giải Toán 6 trang 8 Tập 1 Cánh diều
a) 11 
A;
b) 12 A;
c) 14 A;
d) 19 A.
Lời giải:
a) Ta thấy tập hợp A chứa số 11 hay 11 thuộc tập hợp A nên ta viết: 11 
A;
b) Ta thấy tập hợp A không chứa 12 hay 12 không thuộc tập hợp A nên ta viết: 12 
A;
c) Ta thấy tập hợp A không chứa 14 hay 14 không thuộc tập hợp A nên ta viết: 14 A;
d) Ta thấy tập hợp A chứa số 19 hay 19 thuộc tập hợp A nên ta viết: 19 A.
a) A = {x | x là số tự nhiên chẵn, x < 14};
b) B = {x | x là số tự nhiên chẵn, 40 < x < 50};
c) C = {x | x là số tự nhiên lẻ, x < 15};
d) D = {x | x là số tự nhiên lẻ, 9 < x < 20}.
Lời giải:
a) A = {x | x là số tự nhiên chẵn, x < 14}
Ta thấy tập hợp A gồm các số tự nhiên chẵn nhỏ hơn 14 nên các phần tử thuộc tập hợp A là: 0; 2; 4; 6; 8; 10; 12.
Vậy ta viết tập hợp A là:
A = {0; 2; 4; 6; 8; 10; 12}.
b) B = {x | x là số tự nhiên chẵn, 40 < x < 50}
Ta thấy tập hợp B gồm các số tự nhiên chẵn lớn hơn 40 và nhỏ hơn 50 nên các phần tử thuộc tập hợp B là: 42; 44; 46; 48.
Vậy ta viết tập hợp B là:
B = {42; 44; 46; 48}.
c) C = {x | x là số tự nhiên lẻ, x < 15};
Ta thấy tập hợp C là các số tự nhiên lẻ nhỏ hơn 15 nên các phần tử thuộc tập hợp C là 1; 3; 5; 7; 9; 11; 13.
Do đó ta viết tập hợp C là:
C = {1; 3; 5; 7; 9; 11; 13}.
d) D = {x | x là số tự nhiên lẻ, 9 < x < 20}.
Ta thấy tập hợp D là các số tự nhiên lẻ lớn hơn 9 và nhỏ hơn 20 nên các phân tử thuộc tập hợp D là: 11; 13; 15; 17; 19.
Do đó ta viết tập hợp D là:
D = {11; 13; 15; 17; 19}.
a) A = {0; 3; 6; 9; 12; 15};
b) B = {5; 10; 15; 20; 25; 30};
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90};
d) D = {1; 5; 9; 13; 17}.
Lời giải:
a) A = {0; 3; 6; 9; 12; 15};
Ta thấy các số 0; 3; 6; 9; 12; 15 là các số tự nhiên chia hết cho 3 và nhỏ hơn 16 nên ta viết tập hợp A bằng cách chỉ ra tính chất đặc trưng là:
A = {x | x là số tự nhiên chia hết cho 3, x < 16}.
b) B = {5; 10; 15; 20; 25; 30};
Ta thấy các số 5; 10; 15; 20; 25; 30 là các số tự nhiên chia hết cho 5, lớn hơn 0 và nhỏ hơn 31 (hoặc ta có thể viết nhỏ hơn 32; …; 35).
Vậy ta có thể viết tập hợp B bằng các cách sau:
Cách 1:
B = {x | x là các số tự nhiên chia hết cho 5, 0 < x < 31}.
Cách 2:
B = {x | x là các số tự nhiên chia hết cho 5, 0 < x < 35}…
c) C = {10; 20; 30; 40; 50; 60; 70; 80; 90};
Ta thấy các số 10; 20; 30; 40; 50; 60; 70; 80; 90 là các số tự nhiên chia hết cho 10, lớn hơn 0 và nhỏ hơn 100 (hoặc ta có thể viết nhỏ hơn 91; …; 99).
Vậy ta có thể viết tập hợp C bằng các cách sau:
Cách 1:
C = {x | x là các số tự nhiên chia hết cho 10, 0 < x < 91}.
Cách 2:
C = {x | x là các số tự nhiên chia hết cho 10, 0 < x < 100}…
d) D = {1; 5; 9; 13; 17}
Ta thấy các số 1; 5; 9; 13; 17 là các số tự nhiên thỏa mãn số sau hơn số trước 4 đơn vị (hay còn gọi là hơn kém nhau 4 đơn vị) bắt đầu từ 1 và nhỏ hơn 18.
Do đó ta viết tập hợp D là:
D = {x | x là các số tự nhiên hơn kém nhau 4 đơn vị bắt đầu từ 1, x < 18}.
Có thể em chưa biết (trang 8)
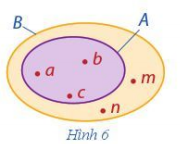
b) Quan sát Hình 6 và cho biết phát biểu nào sau đây là đúng:
1. a ∉ B;
2. m ∈ A;
3. b ∈ B;
4. n ∉ A.
Lời giải:
a) Ta thấy trong biểu đồ Ven minh họa tập hợp A, các phần tử a, b, c nằm trong vòng kín
Vậy ta viết tập hợp A là: A = {a; b; c}.
Tương tự, ta thấy các phần tử a, b, c, m, n đều nằm trong vòng kín của biểu đồ Ven minh họa tập hợp B
Do đó ta viết tập hợp B là: B = {a; b; c; m; n}.
b) Ta thấy,
+ Tập hợp B chứa phần tử a nên a ∈ B nên 1 sai.
+ Tập hợp A không chứa phần tử m nên m ∉ A nên 2 sai.
+ Tập hợp B chứa phần tử b nên b ∈ B nên 3 đúng.
+ Tập hợp A không chứa phần tử n nên n ∉ A nên 4 đúng.
Vậy phát biểu 3 và 4 là phát biểu đúng.
Lời giải:
Do tất cả các học sinh của lớp 6A đều biết chơi bóng rổ hoặc cờ vua nên số học sinh nhiều nhất của 6A là:
18 + 23 = 41 (học sinh)
Vậy số học sinh của lớp 6A nhiều nhất là 41 học sinh.
Lý thuyết Tập hợp
1. Tập hợp
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
Ví dụ:
+ Tập hợp các đồ vật (sách, bút) đặt trên bàn.
+ Tập hợp học sinh lớp 6A.
+ Tập hợp các số tự nhiên nhỏ hơn 7.
+ Tập hợp các số trên mặt đồng hồ trong hình dưới
2. Kí hiệu và cách viết tập hợp
Tên tập hợp được viết bằng chữ cái in hoa như: A, B, C,…
Ví dụ:
+ Tập hợp A gồm các số tự nhiên nhỏ hơn 5
Ta viết: A = {0; 1; 2; 3; 4}
Các số 0; 1; 2; 3; 4 được gọi là các phần tử của tập hợp A.
+ Tập hợp B = {bóng rổ; bóng đá; cầu lông; bóng bàn}
Các phần của tập hợp B là: bóng rổ, bóng đá, cầu lông, bóng bàn.
Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
Chẳng hạn, với tập A ở trên, ta có thể viết như sau:
A = {2; 3; 1; 4; 0}
3. Phần tử thuộc tập hợp
Kí hiệu: ∈ (thuộc) và ∉ (không thuộc)
Ví dụ: Cho tập hợp B = {2; 3; 5; 6}
- Các số 2; 3; 5; 6 là các phần tử của tập hợp B, ta nói
+ Phần tử 2 (số 2) thuộc tập hợp B, viết là 2 ∈ B
+ Phần tử 3 (số 3) thuộc tập hợp B, viết là 3 ∈ B
+ Phần tử 5 (số 5) thuộc tập hợp B, viết là 5 ∈ B
+ Phần tử 6 (số 6) thuộc tập hợp B, viết là 6 ∈ B
- Ta thấy số 4 không là phần tử của tập hợp B, ta viết 4 ∉ B, đọc là 4 không thuộc B.
4. Cách cho tập hợp
Có hai cách cho một tập hợp
4.1 Liệt kê các phần tử của tập hợp.
Ví dụ: Quan sát các số được cho ở hình dưới:
Gọi A là tập hợp các số đó.
Các phần tử của tập hợp A là: 0; 1; 2; 3; 4
Ta viết: A ={0; 1; 2; 3; 4} .
4.2 Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ví dụ:Các phần tử của tập hợp A ở trên đều là các số tự nhiên nhỏ hơn 5. Ta có thể viết:
A = {x| x là số tự nhiên nhỏ hơn 5}.
4.3 Chú ý:
• Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu ";".
• Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy ý.
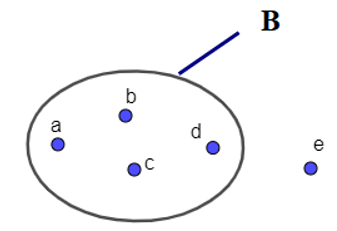
• Ngoài ra ta còn minh họa tập hợp bằng một vòng tròn kín, mỗi phần tử của tập hợp được biểu diễn bằng 1 dấu chấm bên trong vòng tròn kín đó, còn phần tử không thuộc tập hợp được biểu diễn bởi một dấu chấm bên ngoài vòng kín. Cách minh họa tập hợp như trên gọi là biểu đồ Ven (Venn).
Ví dụ: Tập hợp B trong hình vẽ là B = {a; b; c; d}; e ∉ B
Xem thêm các bài giải SGK Toán lớp 6 Cánh diều hay, chi tiết khác:
Bài 2: Tập hợp các số tự nhiên
Bài 3: Phép cộng, phép trừ các số tự nhiên
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
