Với tóm tắt lý thuyết Toán lớp 5 Bài 27: Đường tròn. Chu vi và diện tích hình tròn sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc, có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 5.
Lý thuyết Toán lớp 5 Bài 27: Đường tròn. Chu vi và diện tích hình tròn
A. Lý thuyết Đường tròn. Chu vi và diện tích hình tròn
1. Đường tròn. Vẽ đường tròn có tâm và bán kính cho trước
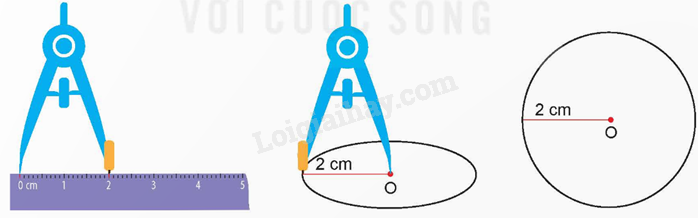
* Dùng com pa để vẽ đường tròn tâm O bán kính 2 cm.
|
Đặt một đầu com pa ở vị trí vạch 0 cm của thước kẻ, đầu còn lại ở vị trí vạch 2 cm của thước kẻ. • Trên tờ giấy, đặt đầu nhọn com pa tại điểm O, sau đó quay com pa một vòng. • Đầu chì vạch trên tờ giấy đường tròn tâm O bán kính 2 cm. |
2. Chu vi hình tròn
|
Muốn tính chu vi hình tròn, ta lấy số 3,14 nhân với đường kính. Hoặc: Muốn tính chu vi hình tròn, ta lấy số 3,14 nhân với bán kính rồi nhân với 2.
Trong đó: C là chu vi hình tròn, d là đường kính hình tròn, r là bán kinh hình tròn. |
Ví dụ:
Chu vi hình tròn đường kính 2 dm là:
3,14 x 2 = 6,28 (dm)
Chu vi hình tròn bán kính 5 m là:
3,14 x 5 x 2 = 31,4 (m).
3. Diện tích hình tròn
|
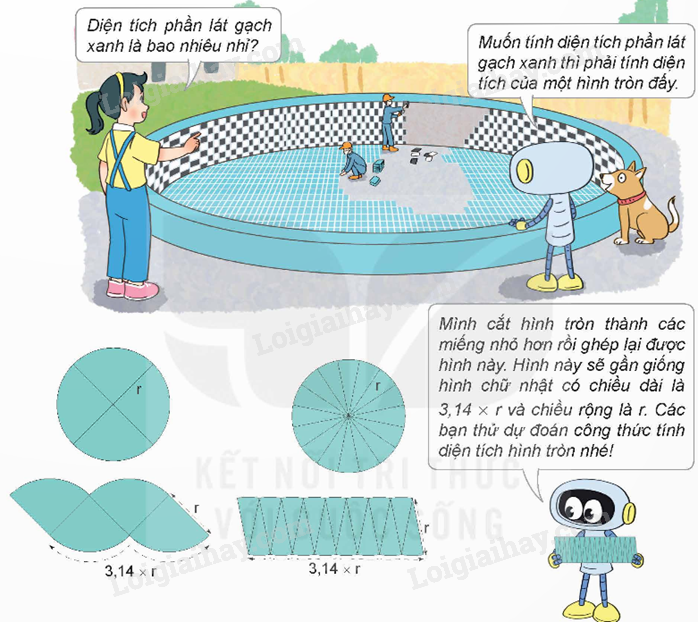
Muốn tính diện tích hình tròn ta lấy số 3,14 nhân với bán kính rồi nhân với bán kính:
Trong đó: S là diện tích hình tròn, r là bán kính hình tròn. |
Ví dụ:
Diện tích hình tròn bán kính 10 cm là:
3,14 x 10 x 10 = 314 (cm²).
B. Bài tập Đường tròn. Chu vi và diện tích hình tròn
Đang cập nhật …
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 5 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
