Với giải sách bài tập Toán 6 Bài 3: Vai trò của tính đối xứng trong thế giới tự nhiên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 3: Vai trò của tính đối xứng trong thế giới tự nhiên

Bài 1 trang 76 sách bài tập Toán lớp 6 Tập 2: Khi quan sát sự di chuyển và hình dạng đối xứng của các động vật, con người đã chế tạo ra các công cụ hữu ích như chiếc xe, chiếc máy bay chiếc tàu ngầm. Em hãy tìm hình minh hoạ và nêu ví dụ cụ thể về điều này.

Lời giải:

Chỉ ra điểm chung về hình dạng của một công cụ hữu ích với động vật nào đó.

Ví dụ: Chiếc máy bay và con chim.

Hình minh hoạ:

Bài 2 trang 76 sách bài tập Toán lớp 6 Tập 2: Hai hình bên dưới là những di tích lịch sử có tính đối xứng. Em hãy chỉ ra tính đối xứng của nó. Hãy cho biết tên các di tích này.

Lời giải:

Hai di tích này đều có trục đối xứng và không có tâm đối xứng được biểu diễn như trên hình.

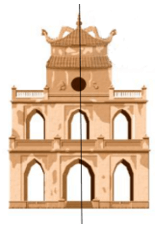
Tên di tích: Hình bên trái là Tháp Rùa ở Hồ Gươm, hình bên phải là ga Đà Lạt.

Bài 3 trang 76 sách bài tập Toán lớp 6 Tập 2: Tìm hai hình di tích lịch sử hoặc công trình kiến trúc có tính đối xứng ở Việt Nam.

Lời giải:

Hai hình di tích lịch sử hoặc công trình kiến trúc có tính đối xứng (đối xứng trục) ở Việt Nam, ví dụ:

Cổng Đền Hùng.

Di tích lịch sử và kiến trúc nghệ thuật Văn Miếu - Quốc Tử Giám.

Bài 4 trang 76 sách bài tập Toán lớp 6 Tập 2: Tìm hai hình di tích lịch sử hoặc công trình kiến trúc có tính đối xứng ở quê hương em.

Lời giải:

Tìm các di tích, công trình kiến trúc ở quê hương em, chú ý các cổng hoặc cầu (thường có tính đối xứng).

Bài 5 trang 77 sách bài tập Toán lớp 6 Tập 2: Các bông hoa và chiếc lá dưới đây, hình nào có tính đối xứng (đối xứng trục hay đối xứng tâm)?

a) 

b) 

c) 

Lời giải:

Một đường thẳng là trục đối xứng nếu gấp hình theo đường đó, ta được 2 phần chồng khít lên nhau.

I là tâm đối xứng của hình H nếu I là trung điểm của đoạn thẳng nối hai điểm tương ứng bất kì trên H.

Bông hoa ở hình a) vừa có trục đối xứng và tâm đối xứng.

Hình minh họa một trục đối xứng của bông hoa hình a) và tâm đối xứng là tâm của nhụy hoa

Chiếc lá ở hình b) có trục đối xứng nhưng không có tâm đối xứng.

Hình minh họa một trục đối ứng của chiếc lá trong hình b)

Bông hoa ở hình c) có tâm đối xứng nhưng không có trục đối xứng.

Hình minh họa một trục đối xứng của bông hoa hình c)

Bài 6 trang 77 sách bài tập Toán lớp 6 Tập 2: Hãy tìm hình bông hoa và chiếc lá có tính đối xứng.

Lời giải:

Những bông hoa và chiếc lá có tính đối xứng là:

Hoa phong lan có trục đối xứng.

Hoa râm bụt có trục đối xứng.

Hoa hướng dương vừa có trục đối xứng vừa có tâm đối xứng.

Lá phong có trục đối xứng.

Bài 7 trang 77 sách bài tập Toán lớp 6 Tập 2: Hãy chỉ ra các trục đối xứng và tâm đối xứng (nếu có) của mỗi hình sau.

a) 

b) 

Lời giải:

Gập đôi hình sao cho hai phần trùng khít lên nhau, nếp gấp đó chính là trục đối xứng.

I là tâm đối xứng của hình H nếu I là trung điểm của đoạn thẳng. Nối hai điểm tương ứng bất kì trên H.

Hình a) vừa có tâm đối xứng vừa có trục đối xứng (như hình vẽ).

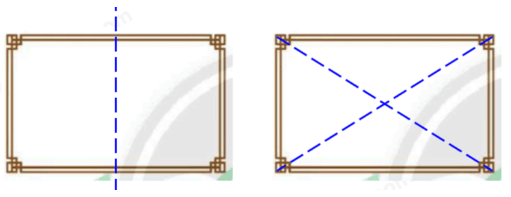
Hình b) vừa có tâm đối xứng vừa có trục đối xứng (như hình vẽ).