Với giải sách bài tập Toán 6 Bài 1: Hình có trục đối xứng sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 1: Hình có trục đối xứng

Bài 1 trang 71 sách bài tập Toán lớp 6 Tập 2: Vẽ trục đối xứng của mỗi hình sau:

a)

b)

c) 

Lời giải:

Trục đối xứng là đường thẳng mà khi gấp hình theo đường đó ta được hai phần chồng khít lên nhau.

Các đường nét đứt là trục đối xứng của mỗi hình.

Hình a) có một trục đối xứng được biểu diễn như hình sau:

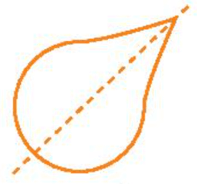
Hình b) có một trục đối xứng được biểu diễn như hình sau:

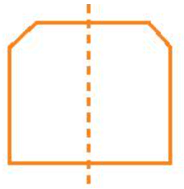
Hình c) có bốn trục đối xứng được biểu diễn như các hình sau:

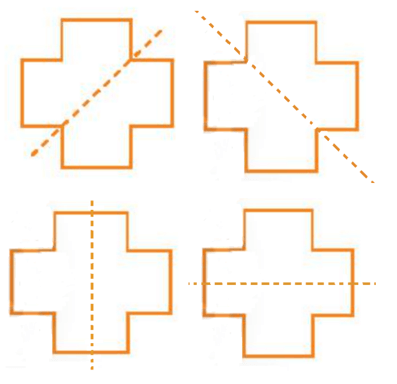
Bài 2 trang 71 sách bài tập Toán lớp 6 Tập 2: Hình nào sau đây có đường nét đứt là trục đối xứng.

Lời giải:

Hình a), b), d) có đường nét đứt chia hình đó thành hai phần bằng nhau nên những hình này có trục đối xứng.

Hình c) có đường nét đứt chia hình đó thành hai phần không bằng nhau nên hình này không có trục đối xứng.

Vậy hình a), b), d) có đường nét đứt là trục đối xứng.

Bài 3 trang 71 sách bài tập Toán lớp 6 Tập 2: Mỗi hình sau đây có bao nhiêu trục đối xứng?

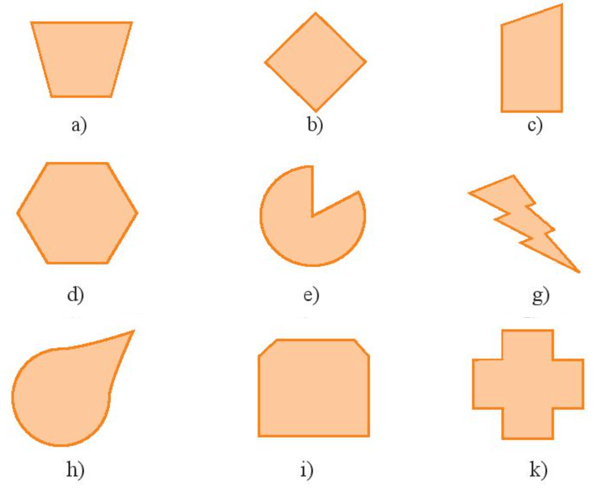
Lời giải:

Trục đối xứng là số đường thẳng chia hình đó thành hai phần bằng nhau (giống hệt nhau).

Số các trục đối xứng của các hình được biểu diễn như sau:

Hình a) có 1 trục đối xứng.

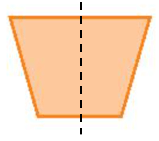
Hình b) có 4 trục đối xứng.

Hình c) không có trục đối xứng.

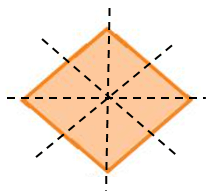
Hình d) có 6 trục đối xứng.

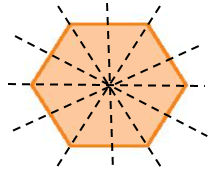
Hình e) có 1 trục đối xứng.

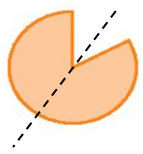
Hình g) không có trục đối xứng.

Hình h) có 1 trục đối xứng.

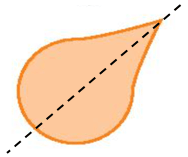
Hình i) có 1 trục đối xứng.

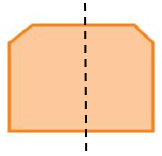
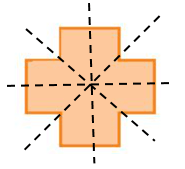
Hình k) có 4 trục đối xứng.

Vậy số các trục đối xứng trong mỗi hình như sau:

Bài 4 trang 72 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ trục một đối xứng của mỗi hình sau (có thể):

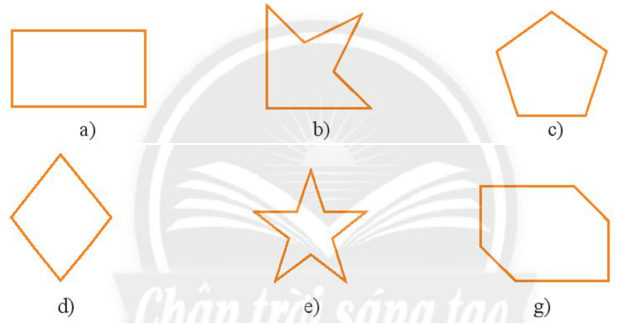
Lời giải:

Một trục đối xứng của các hình được biểu diễn như sau:

Hình a) 

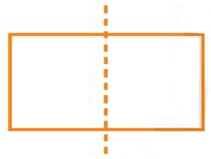
Hình b)

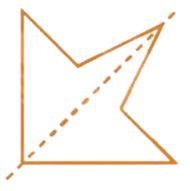
Hình c)

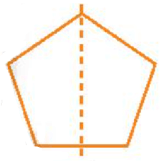
Hình d)

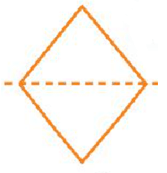
Hình e)

Hình g) không có trục đối xứng.

Bài 5 trang 72 sách bài tập Toán lớp 6 Tập 2: Hãy vẽ trục đối xứng của mỗi hình sau nếu có thể:

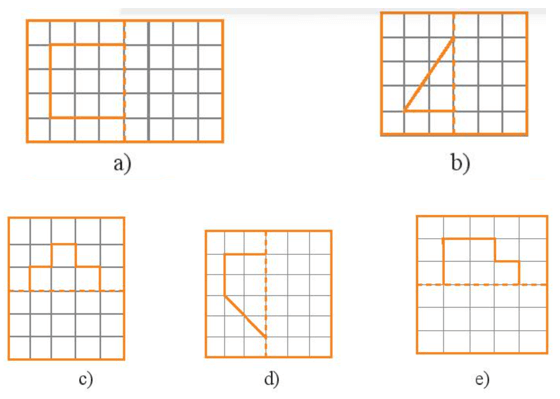
Lời giải:

Coi đường nét đứt như một cái gương, vẽ thêm sao cho khi gập hình theo đường nét đứt ta được hai phần giống hệt và chồng khít lên nhau.

Hình sau khi được vẽ thêm có đường nét đứt là trục đối xứng được biểu diễn như sau:

Hình a)

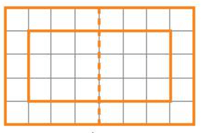
Hình b)

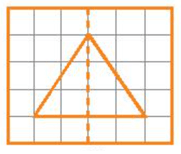
Hình c)

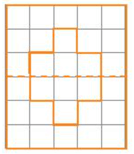
Hình d)

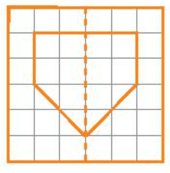
Hình e)

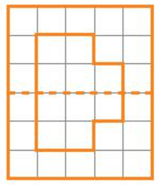
Lý thuyết Hình có trục đối xứng

Hình có trục đối xứng. Trục đối xứng

Có một đường thẳng d chia hình thành hai phần mà khi ta gấp hình theo đường thẳng d thì hai phần đó chồng khít lên nhau.

Những hình như thế là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.

Ví dụ. Hình vẽ sau là hình có trục đối xứng và đường nét đứt là trục đối xứng của hình.

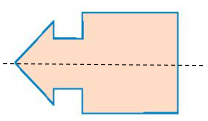
Khi đó, ta gấp hình trên theo đường nét đứt thì ta được hai phần chồng khít lên nhau.