Với giải sách bài tập Toán 6 Bài ôn tập chương 2 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài ôn tập chương 2

Bài 1 trang 57 sách bài tập Toán lớp 6 Tập 1: Tính:

a) 173 - (12 - 29);

b) (-255) - (77 - 22)

c) (-66).5

d) (-340).(-300)

Lời giải:

a) 173 - (12 - 29) 

= 173 – [-(29 – 12)]

= 173 – (-17)

= 173 + 17

= 190

b) (-255) - (77 - 22) 

= (-255) – 55

= - (255 + 55) 

= - 310.

c) (-66).5 = - 66.5 = - 330.

d) (-340).(-300) = 340.300 = 102 000.

Bài 2 trang 57 sách bài tập Toán lớp 6 Tập 1: Tính:

a) (-12).(-10).(-7)

b) (25 + 38) : (-9)

c) (38 - 25).(-17 + 12)

d) 40 : (-3 - 7) + 9

Lời giải:

a) (-12).(-10).(-7) = [(-12).(-7)].(-10) = 84.(-10) = - 84.10 = -840.

b) (25 + 38) : (-9) = 63: (-9) = -7.

c) (38 - 25).(-17 + 12) = 13.(-5) = - 65.

d) 40 : (-3 - 7) + 9 = 40: (-10) + 9 = (-4) + 9 = 5.

Bài 3 trang 57 sách bài tập Toán lớp 6 Tập 1: Tìm các số nguyên x thỏa mãn:

a) x² = 9;

b) x² = 100.

Lời giải:

a) x² = 9

⇔ x² = (-3)² hoặc x² = 3²

⇔ x = - 3 hoặc x = 3 

Vậy x = -3 hoặc x = 3.

b) x² = 100

⇔ x² = (-10)² hoặc x² = 10²

⇔ x = - 10 hoặc x = 10 

Vậy x = -10 hoặc x = 10.

Bài 4 trang 57 sách bài tập Toán lớp 6 Tập 1: Liệt kê và tính tổng tất cả các số nguyên x thỏa mãn:

a) -7 < x < 6

b) -4 ≤ x ≤ 4

c) -8 < x < 8

Lời giải:

a) Ta có số nguyên x thỏa mãn -7 < x < 6 nên x ∈ {-6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5}

Tổng của các số thỏa mãn bài toán là:

T = (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 

= (-6) + [(-5) + 5] + [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0 

= (-6) + 0 + 0 + 0 + 0 + 0 + 0 

= -6.

Vậy tổng các số nguyên x thỏa mãn điều kiện – 7 < x < 6 là -6.

b) Ta có số nguyên x thỏa mãn -4 ≤ x ≤ 4 nên x ∈ {-4; -3; -2; -1; 0; 1; 2; 3; 4}

Tổng của các số thỏa mãn bài toán là:

T = (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 

= [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0 

= 0 + 0 + 0 + 0 + 0

= 0.

Vậy tổng các số nguyên thỏa mãn điều kiện -4 ≤ x ≤ 4 là 0.

c) Ta có các số nguyên x thỏa mãn -8 < x < 8 nên x ∈ {-7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7}

Tổng của các số thỏa mãn bài toán là:

T = (-7) + (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7

= [(-7) + 7] + [(-6) + 6] + [(-5) + 5] + [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0 

= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0

= 0.

Vậy tổng các số nguyên x thỏa mãn điều kiện – 8 < x < 8 là 0.

Bài 5 trang 57 sách bài tập Toán lớp 6 Tập 1: Tính theo hai cách:

a) 18.15 - 3.6.10

b) 63 - 9.(12 + 7)

c) 39.(29 - 13) - 29.(39-13)

Lời giải:

a) Cách 1: 18.15 - 3.6.10 

= 18.15 - 18.10 

= 18.(15 - 10) 

= 18.5 

= 90

Cách 2: 18.15 - 3.6.10 

= 270 - 180 

= 90

b) Cách 1: 63 - 9.(12 + 7) 

= 63 - 9.12 - 9.7 

= 63  - 108 - 63 

= (63 – 63) – 108

= 0 - 108

= -108

Cách 2: 63 - 9.(12 + 7) 

= 63 - 9.19 

= 63 – 171

= -(171 – 63) 

= -108

c) Cách 1: 39.(29 - 13) - 29.(39-13) 

= 39.29 - 39.13 - 29.39 + 29.13 

= (39.29 – 29.39) + (-39.13 + 29.13)

= 0 + (-39).13 + 29.13

= 13.(29 - 39) 

= 13.(-10)

= -130

Cách 2: 39.(29 - 13) - 29.(39-13) 

= 39.16 - 29.26 

= 624 – 754

= -(754 – 624)

= - 130

Bài 6 trang 57 sách bài tập Toán lớp 6 Tập 1: Pythagoras được sinh ra vào khoảng năm 582 trước công nguyên. Isaac Newton sinh năm 1643 sau công nguyên. Họ sinh cách nhau bao nhiêu năm?

Lời giải:

Năm sinh của Pythagoras là: - 582 

Hai người sinh cách nhau số năm là: 1643 - (-582) = 2225 (năm)

Vậy Isaac Newton và Pythagoras sinh cách nhau 2225 năm.

Bài 7 trang 57 sách bài tập Toán lớp 6 Tập 1: Trong điều kiện thời tiết ổn định, cứ tăng độ cao 1km thì nhiệt độ không khí giảm 6⁰C. Một khinh khí cầu đã được phóng lên vào một ngày khô ráo. Nếu nhiệt độ trên mặt đất tại nơi phóng là 18⁰C, thì nhiệt độ là bao nhiêu khi khinh khí cầu ở độ cao 5km?

Lời giải:

Khi khinh khí cầu ở độ cao 5km thì nhiệt độ là: 18 + (-6).5 = 18 – 30 = -12⁰C.

Vậy sau khi lên cao 5km thì nhiệt độ của khinh khí cầu là – 12⁰C.

Bài 8 trang 57 sách bài tập Toán lớp 6 Tập 1: Một tàu ngầm trên mặt đại dương lặn xuống với tốc độ 2m/s trong 2 phút. Sau đó, nó nổi lên với tốc độ 1m/s trong 3 phút. Cuối cùng, nó lặn xuống với tốc độ 3 m/s trong 1 phút. Độ cao cuối cùng của tàu ngầm là bao nhiêu so với bề mặt đại dương?

Lời giải:

Đổi 2 phút = 120 giây, 3 phút = 180 giây, 1 phút = 60 giây.

Cách 1: Độ cao sau khi lặn xuống lần đầu tiên là: (-2).120 = - 240 (m).

Độ cao sau khi nổi lên là: 1.180 = 180 (m).

Độ cao sau khi lặn xuống lần thứ hai là: (-3).60 = - 180 (m).

Độ cao cuối cùng của tàu ngầm là: -240 + 180 + (-180) = - 240 (m).

Vậy tàu ngầm đang ở độ cao - 240m so với bề mặt đại dương.

Cách 2: 

Độ cao cuối cùng của tàu ngầm là:

(-2).120 + 1.180 + (-3).60 = -240 (m)

Vậy tàu ngầm đang ở độ cao - 240m so với bề mặt đại dương.

Bài 9 trang 57 sách bài tập Toán lớp 6 Tập 1: Một tủ cấp đông khi chưa bật tủ thì nhiệt độ bằng 22⁰C. Khi bật tủ đông, nhiệt độ bên trong tủ giảm 2⁰C mỗi phút. Hỏi phải mất bao lâu để tủ đông đạt -10⁰C?

Lời giải:

Cách 1: Tủ cấp đông đã giảm: 22 – (-10) = 22 + 10 = 22⁰C.

Để tủ đông đạt -10⁰C thì mất số thời gian là: 22 : -2 = 16 (phút)

Vậy cần mất 16 phút để tủ đông đạt -10⁰C.

Cách 2: Để tủ đông đạt -10⁰C thì mất số thời gian là: (-10 - 22) : (-2) = 16 (phút)

Vậy cần mất 16 phút để tủ đông đạt -10⁰C.

Bài 10 trang 57 sách bài tập Toán lớp 6 Tập 1: Minh đang chơi một trò chơi tung xúc xắc 6 mặt. Nếu mặt quay lên có chẵn số chấm tròn thì Minh sẽ được số điểm gấp 15 lần số chấm tròn xuất hiện. Nếu nó là số lẻ chấm, Minh sẽ bị trừ điểm gấp 10 lần số chấm tròn xuất hiện. Minh tung xúc xắc ba lần, lần lượt các mặt có số chấm tròn là 3; 6; 5. Tính số điểm Minh đạt được.

Lời giải:

Cách 1: Số điểm Minh đạt được sau lần tung xúc xắc đầu tiên là: 3.(-10) = - 30 điểm.

Sau lần tung thứ hai số điểm Minh đạt được là: 6.15 = 90 điểm.

Sau lần tung thứ ba số điểm Minh đạt được là: 5.(-10) = - 50 điểm.

Sau ba lần tung số điểm của Minh đạt được là: - 30 + 90 + (-50) = 10 điểm.

Vậy sau ba lần tung số điểm của bạn Minh là 10 điểm.

Cách 2: Số điểm Minh đạt được là:

3.(-10) + 6.15 + 5.(-10) = 10 (điểm)

Vậy sau ba lần tung số điểm của bạn Minh là 10 điểm.

Bài 11 trang 58 sách bài tập Toán lớp 6 Tập 1: Bảng dưới đây cho biết nhiệt độ của các hành tinh trong hệ Mặt Trời tại cùng một thời điểm:

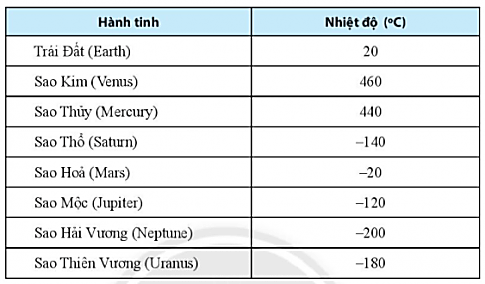
a) Tính số chênh lệch độ của mỗi cặp hành tinh:

• Sao Kim và Trái Đất
• Sao Thủy và Sao Thổ
• Hành tinh nóng nhất và hành tinh lạnh nhất
• Sao Hỏa và Sao Thiên Vương

b)

• Tổng nhiệt độ của Trái Đất và Sao Hải Vương bằng nhiệt độ của hành tinh nào?
• Tổng nhiệt độ của Sao Mộc và Sao Hỏa bằng nhiệt độ của hành tinh nào?
• Có nhận xét gì về tổng nhiệt độ của Sao Mộc, Sao Thổ và Sao Hải Vương với nhiệt độ của Sao Kim?

Lời giải:

a) Độ chênh lệch nhiệt độ của sao Kim và Trái Đất là: 460 - 20 = 440 (⁰C)

Vậy Sao Kim nóng hơn Trái Đất: 440 ⁰C.

Độ chênh lệch nhiệt độ của Sao Thủy và Sao Thổ là: 440 - (-140) = 580 (⁰C)

Vậy Sao Thủy nóng hơn Sao Thổ 580⁰C.

Hành tinh nóng nhất là Sao Kim : 460⁰C

Hành tinh lạnh nhất là Sao Hải Vương: -200⁰C

Độ chênh lệch nhiệt độ của Sao Kim và Sao Hải Vương là: 460 - (-200) = 660 (⁰C)

Vậy Sao Kim nóng hơn Sao Hải Vương: 660 ⁰C.

Độ chênh lệch nhiệt độ của Sao Hỏa và Sao Thiên Vương -20 - (-180) = 160 (⁰C)

Vậy Sao Hỏa nóng hơn Sao Thiên Vương là 160⁰C.

b) Tổng nhiệt độ của Trái Đất và Sao Hải Vương : 20 + (-200) = -180 (⁰C)

Vậy tổng nhiệt độ của Trái Đất và Sao Hải Vương bằng nhiệt độ của Sao Thiên Vương cùng bằng -180⁰C.

Tổng nhiệt độ của Sao Mộc và Sao Hỏa là: -20 + (-120) = -140⁰C

Vậy tổng nhiệt độ của Sao Mộc và Sao Hỏa bằng nhiệt độ của Sao Thổ cùng bằng – 140⁰C.

Tổng nhiệt độ của Sao Mộc, Sao Thổ và Sao Hải Vương là: (-120) + (-140) + (-200) = -460⁰C. 

Nhiệt độ Sao Kim là: 460⁰C.

- 460 và 460 là hai số đối nhau

Vậy tổng nhiệt độ của Sao Mộc, Sao Thổ và Sao Hải Vương và nhiệt độ Sao Kim là hai số đối nhau.

Bài 12 trang 58 sách bài tập Toán lớp 6 Tập 1: a) Dấu của tích hai số nguyên cùng dấu là dương. Dấu của tích ba số nguyên cùng dấu là gì? Giải thích.

b) Tích của hai số nguyên là a và b là 15. Tổng nhỏ nhất của hai số đó bằng bao nhiêu?

Lời giải:

a) Nếu cả ba số nguyên cùng dấu dương thì tích của ba số này sẽ mang dấu dương.

Nếu cả ba số nguyên cùng dấu âm thì tích của ba số này sẽ mang dấu âm.

b) Vì a.b = 15 nên ta có các trường hợp:

1.15;     (-1).(-15);      3.5;      (-3).(-5)

Ta có: 

1 + 15 = 15;

(-1) + (-15) = -16;

3 + 5 = 8;

(-3) + (-5) = -8;

Tổng nhỏ nhất của a và b là a + b = (-1) + (-15) = -16.