Với giải sách bài tập Toán 6 Bài 3: Phép cộng và phép trừ hai số nguyên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 3: Phép cộng và phép trừ hai số nguyên

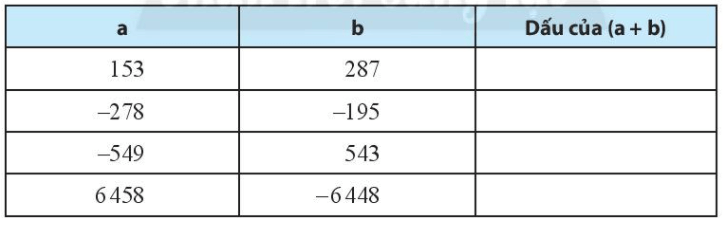
Bài 1 trang 51 sách bài tập Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy điền dấu vào bảng sau:

Lời giải:

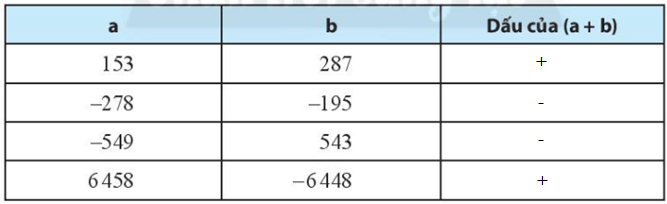
+) Với a = 153, b = 287 là hai số nguyên dương nên dấu của a + b cũng dương.

+) Với a = -278, b = -195 là hai số nguyên âm nên dấu của a + b cũng âm.

+) Với a = -547 là số nguyên âm, b = 543 là số nguyên dương, số đối của a là 547 lớn hơn b nên tổng (a + b) mang dấu của a là dấu âm.

+) Với a = 6 458 là số nguyên dương, b = - 6 448 là số nguyên âm trong đó số đối của b là 6 448 nhỏ hơn a nên tổng (a + b) mang dấu của a là dấu dương.

Khi đó, ta có bảng sau:

Bài 2 trang 51 sách bài tập Toán lớp 6 Tập 1: Điền số thích hợp vào ô trống trong bảng dưới đây:

Lời giải:

+) Với a = -2, b = 12 

Suy ra a + b = (-2) + 12 = 12 – 2 = 10;

+) Với a = -97, b = 97 

Suy ra a + b = (-97) + 97 = 97 – 97 = 0;

+) Với a = 156, a + b = 0

Suy ra b là số đối của a hay b = -a = -156;

+) Với b = 25, a + b = 3 

Suy ra a = 3 – b = 3 – 25 = - (25 – 3) = - 22;

+) Với a = -37, a + b = -50

Suy ra b = - 50 – a = - 50 – (-37) = - 50 + 37 = -(50 – 37) = -13;

Khi đó ta có bảng sau:

Bài 3 trang 52 sách bài tập Toán lớp 6 Tập 1: Thực hiện các phép tính sau:

a) 73 + 47

b) (-13) + (-29)

c) (-132) + (-255)

d) 175 + (-175)

e) 85 + (-54)

g) (-142) + 122

h) 332 + (-735)

Lời giải:

a) 73 + 47 = 120;

b) (-13) + (-29) = - (13 + 29) = - 42;

c) (-132) + (-255) = -(132 + 255) = -387;

d) 175 + (-175) = 175 – 175 = 0;

e) 85 + (-54) = 85 – 54 = 31;

g) (-142) + 122 = -(142 – 122) = - 20;

h) 332 + (-735) = 332 – 735 = - (735 – 332) = - 403.

Bài 4 trang 52 sách bài tập Toán lớp 6 Tập 1: Thực hiện các phép tính sau:

a) 36 - 38

b) 51 - (-49)

c) (-75) - 15

d) 0 - 35

e) (-72) - (-16)

g) 126 - 234

Lời giải:

a) 36 - 38 = - (38 – 36) =  -2;

b) 51 - (-49) = 51 + 49 = 100;

c) (-75) - 15 = - (75 + 15) = -90;

d) 0 - 35 = - (35 – 0) = -35; 

e) (-72) - (-16) = -72 + 16 = - (72 – 16) = -56;

g) 126 - 234 = - (234 – 126) = - 108.

Bài 5 trang 52 sách bài tập Toán lớp 6 Tập 1: Bỏ dấu ngoặc rồi tính:

a) (29 + 37 + 13) + (10 - 37 - 13);

b) (79 + 32 - 35) - (69 + 12 - 75);

c) -(-125 + 63 + 57) - (10 - 83 - 37).

Lời giải:

a) (29 + 37 + 13) + (10 - 37 - 13)

 = 29 + 37 + 13 + 10 - 37 - 13

 = (37 – 37) + (13 – 13) + (29 + 10)

 = 39

b) (79 + 32 - 35) - (69 + 12 - 75)

 = 79 + 32 - 35 - 69 - 12 + 75

 = (79 – 69) + (32 – 12) + (75 – 35)

 = 10 + 20 + 40

 = 70

c) -(-125 + 63 + 57) - (10 - 83 - 37)

 = 125 - 63 - 57 - 10 + 83 + 37

 = (125 – 10) + (83 + 37) + (- 63 – 57)

 = 115 + 120 - 120

 = 115

Bài 6 trang 52 sách bài tập Toán lớp 6 Tập 1: Thực hiện các phép tính sau một cách hợp lí:

a) 434 + (-100) + (-434) + 700;

b) 6 830 + (-993) + 170 + (-5 007);

c) 31 + 32 + 33 + 34 + 35 - 11 - 12 - 13 - 14 – 15.

Lời giải:

a) 434 + (-100) + (-434) + 700

 = [434 + (-434)] + [700 + (-100)]

 = 0 + 600

= 600

b) 6 830 + (-993) + 170 + (-5 007)

 = (6 830 + 170) + [(-993) + (-5 007)]

 = 7 000 + (-6 000)

= 7 000 – 6 000

= 1 000.

c) 31 + 32 + 33 + 34 + 35 - 11 - 12 - 13 - 14 - 15

 = (31 – 11) + (32 – 12) + (33 – 13) + (34 – 14) + (35 – 15)

 = 20 + 20 + 20 + 20 + 20

= 20.5

= 100.

Bài 7 trang 52 sách bài tập Toán lớp 6 Tập 1: Tính nhanh các tổng sau:

a) (67 – 5 759) + 5759

b) (-3 023) - (765 – 3 023)

c) 631 + [587 - (287 + 231)]

d) (-524) - [(467 + 245) - 45]

Lời giải:

a) (67 - 5759) + 5759 

= 67 - 5759 + 5759 

= 67 + (- 5759) + 5759 

= 67 + [(- 5759) + 5759]

= 67 + 0 

= 67

b) (-3023) - (765 - 3023) 

= -3023 - 765 + 3023 

= [(-3 023) + 3 023] – 765

= 0 – 765

= -765

c) 631 + [587 - (287 + 231)] 

= 631 + (587 - 287 - 231)

= 631 + 587 - 287   - 231

= (631 – 231) + (587 – 287)

= 400 + 300  

= 700

d) (-524) - [(467 + 245) - 45]

= (-524) – [467 + 245 – 45]

= (-524) – 467 – 245 + 45

= [(-524) – 467] + (-245 + 45)

= [(-524) + (-467)] + [-(245 - 45)]

= - 1 000 + (-200)

 = -1200.

Bài 8 trang 52 sách bài tập Toán lớp 6 Tập 1: Thủy ngân là một kim loại ở thể lỏng trong điều kiện nhiệt độ thông thường. Nhiệt độ nóng chảy của thủy ngân là – 39⁰C. Nhiệt độ sôi của thủy ngân là 357⁰C. Tính số độ chênh lệch giữa nhiệt độ sôi và nhiệt độ nóng chảy của thủy ngân.

Lời giải:

Số độ chênh lệch giữa nhiệt độ sôi và nhiệt độ nóng chảy của thủy ngân là:

357 – (– 39) = 357 + 39 = 396⁰C.

Vậy sự chênh lệch giữa nhiệt độ sôi và nhiệt độ nóng chảy của thủy ngân là 396⁰C.

Bài 9 trang 52 sách bài tập Toán lớp 6 Tập 1: Vào một buổi trưa nhiệt độ ở New York (Niu Óoc) là – 5⁰C. Nhiệt độ đêm hôm đó ở New York là bao nhiêu, biết nhiệt độ đêm đó giảm 7⁰C?

Lời giải:

Nhiệt độ đêm hôm đó là: - 5 – 7 = - (5 + 7) = -12⁰C.

Vậy nhiệt độ đêm hôm đó là: -12⁰C.

Bài 10 trang 53 sách bài tập Toán lớp 6 Tập 1: Tính tổng các số nguyên x thỏa mãn mỗi điều kiện sau:

a) -7 < x < 8

b) -10 < x < 9

c) -12 < x < 12

d) -15 ≤ x < 15

Lời giải:

a) Ta có -7 < x < 8 nên x ∈ {-6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7}

Do đó tổng các số nguyên thỏa mãn điều kiện là 

T = (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7

= [(-6) + 6] + [(-5) + 5] + [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0 + 7

= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 7

= 7.

Vậy tổng các số nguyên thỏa mãn điều kiện – 7 < x < 8 là 7.

b) Vì số nguyên x thỏa mãn -10 < x < 9 nên x ∈ {-9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7; 8}

Khi đó tổng các số nguyên trên là: 

T = (-9) + (-8) + (-7) + (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8

= (-9) + [(-8) + 8] + [(-7) + 7] + [(-6) + 6] + [(-5) + 5] + [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0 

= (-9) + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0

= -9.

Vậy tổng các số nguyên thỏa mãn -10 < x < 9 là -9.

c) Ta có số nguyên x thỏa mãn -12 < x < 12 nên x ∈ {-11; -10; -9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11}

Khi đó tổng các số nguyên trên là: 

T = (-11) + (-10) + (-9) + (-8) + (-7) + (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11

= [(-11) + 11] + [(-10) + 10] + [(-9) + 9] + [(-8) + 8] + [(-7) + 7] + [(-6) + 6] + [(-5) + 5] + [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0

= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0

= 0.

Vậy tổng của các số nguyên thỏa mãn – 12 < x < 12 là 0.

d) Ta có số nguyên x thỏa mãn -15 ≤ x < 15 nên x ∈ {-15; -14; -13; -12; -11; -10; -9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13;  14}.

Khi đó tổng các số nguyên trên là: 

T = (-15) + (-14) + (-13) + (-12) + (-11) + (-10) + (-9) + (-8) + (-7) + (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14

= (-15) + [(-14) + 14] + [(-13) + 13] + [(-12) + 12] + [(-11) + 11] + [(-10) + 10] + [(-9) + 9] + [(-8) + 8] + [(-7) + 7] + [(-6) + 6] + [(-5) + 5] + [(-4) + 4] + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0

= (-15) + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0

= -15.

Vậy tổng của các số nguyên thỏa mãn  là 0.

Bài 11 trang 53 sách bài tập Toán lớp 6 Tập 1: Trong bóng đá, nhiều trường hợp để xếp hạng các đội bóng sau một mùa giải, người ta phải tính kết quả của hiệu số bàn thắng - thua. Hãy tính hiệu số bàn thắng - thua của các đội bóng đá nam trong bảng dưới đây:

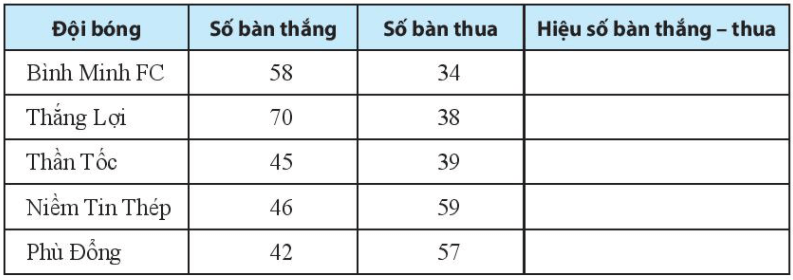
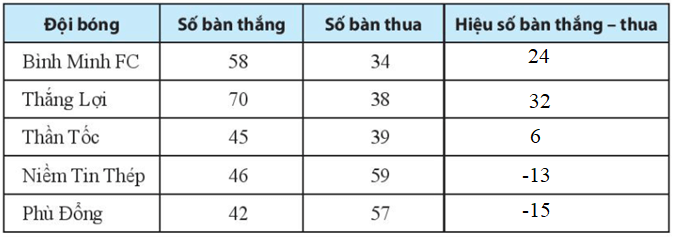
Lời giải:

Hiệu số bàn thắng thua của đội bóng Bình Minh FC là: 58 – 34 = 24 (bàn);

Hiệu số bàn thắng thua của đội bóng Thắng Lợi là: 70 – 38 = 48 (bàn);

Hiệu số bàn thắng thua của đội Thần Tốc là: 45 – 39 = 6 (bàn);

Hiệu số bàn thắng thua của đội Niềm Tin Thép là 46 – 59 = - (59 – 46) = - 13 (bàn);

Hiệu số bàn thắng thua của đội Phù Đổng là: 42 – 57 = - (57 – 42) = - 15 (bàn).

Khi đó ta có bảng sau:

Bài 12 trang 53 sách bài tập Toán lớp 6 Tập 1: Hai số nguyên có một chữ số có tổng bằng -9. Hãy tìm hai số đó. Bài toán có bao nhiêu đáp số?

Lời giải:

Ta có các số nguyên thỏa mãn đề bài:

(-9) + 0 = -9

(-8) + (-1) = -9

(-7) + (-2) = -9

(-6) + (-3) = -9

(-5) + (-4) = -9

Vậy bài toán có 5 đáp số.

Lý thuyết Phép cộng và phép trừ hai số nguyên

1. Cộng hai số nguyên cùng dấu

− Muốn cộng hai số nguyên dương, ta cộng chúng như cộng hai số tự nhiên.

− Muốn cộng hai số nguyên âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đằng trước kết quả.

− Tổng của hai số nguyên cùng dấu luôn cùng dấu với hai số nguyên đó.

Chú ý:

Cho a, b là hai số nguyên dương, ta có:

(+a) + (+b) = a + b

(−a) + (− b) = − (a + b)

Ví dụ: Thực hiện các phép tính sau:

a) 8 + 12;

b) (−15) + (−9);

c) (−65) + (−35).

Hướng dẫn giải

a) 8 + 12 = 11;

b) (−15) + (−9) = − (15 + 9) = −24;

c) (−65) + (−35) = − (65 + 35) = −100.

2. Cộng hai số nguyên khác dấu

a) Cộng hai số đối nhau

Tổng hai số nguyên đối nhau luôn luôn bằng 0: a + (− a) = 0.

Ví dụ: 20 và −20 là hai số đối nhau.

Khi đó, 20 + (− 20) = 0.

b) Cộng hai số nguyên khác dấu không đối nhau

Muốn cộng hai số nguyên khác dấu không đối nhau, ta làm như sau:

− Nếu số dương lớn hơn số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.

− Nếu số dương bé hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ trước kết quả.

Chú ý: Khi cộng hai số nguyên trái dấu:

− Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.

− Nếu số dương bằng số đối của số âm thì ta có tổng bằng 0.

− Nếu số dương bé hơn số đối của số âm thì ta có tổng âm.

Ví dụ: Thực hiện các phép tính sau:

a) 18 + (−21);

b) (−6) + 12;

c) 25 + (−14).

Hướng dẫn giải

a) 18 + (−21) = − (21 – 18) = − 3;

b) (−6) + 12 = 12 – 6 = 6;

c) 25 + (−14) = 25 – 14 = 11.

3. Tính chất của phép cộng các số nguyên

a) Tính chất giao hoán

Phép cộng các số nguyên có tính chất giao hoán, nghĩa là: a + b = b + a

Chú ý: a + 0 = 0 + a = a.

Ví dụ:

25 + 18 = 18 + 25;

16 + (−35) = (−35) + 16;

(−26) + (−47) = (−47) + (−26).

b) Tính chất kết hợp

Phép cộng các số nguyên có tính chất kết hợp: (a + b) + c = a + (b + c)

Chú ý:

− Tổng (a + b) + c hoặc a + (b + c) là tổng của ba số nguyên a, b, c và viết là a + b + c; với a, b, c là các số hạng của tổng.

− Để tính tổng của nhiều số, ta có thể thay đổi tùy ý thứ tự các số hạng (tính giao hoán), hoặc nhóm tùy ý các số hạng (tính kết hợp) để việc tính toán được đơn giản và thuận lợi hơn.

Ví dụ: Thực hiện các phép tính sau:

a) 25 + (−75) + (−25) + 75;

b) (−2 022) + 2 021 + 21 + (−20).

Hướng dẫn giải

a) 25 + (−75) + (−25) + 75

= 25 + (−25) + (−75) + 75 (tính chất giao hoán)

= [25 + (−25)] + [(−75) + 75] (tính chất kết hợp)

= 0 + 0 = 0.

b) (−2 022) + 2 021 + 21 + (−20)

= (−2 022) + (−20) + 2 021 + 21 (tính chất giao hoán)

= [(−2 022) + (−20)] + (2021 + 21) (tính chất kết hợp)

= (−2042) + 2042 = 0.

4. Phép trừ hai số nguyên

Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b.

a – b = a + (−b)

Chú ý:

− Cho hai số nguyên a và b. Ta gọi a – b là hiệu của a và b (a được gọi là số bị trừ, b là số trừ).

− Phép trừ luôn thực hiện được trong tập hợp số nguyên.

Như vậy, hiệu của hai số nguyên a và b là tổng của a và số đối của b.

Ví dụ: Thực hiện các phép tính sau:

a) 5 – 11;

b) 26 – (–12);

c) (–38) – (–50).

Hướng dẫn giải

a) 5 – 11 = 5 + ( −11) = −6;

b) 26 – (–12) = 26 + 12 = 38;

c) (–38) – (–50) = (−38) + 50 = 50 – 38 = 12.

5. Quy tắc dấu ngoặc

Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:

• có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc

+ (a + b – c) = a + b – c

• có dấu “–”, thì phải đổi dấu tất cả các số hạng trong ngoặc

− (a + b – c) = − a − b + c

Ví dụ: Tính M = (− 25) + (−2) – (−75) + (−8).

Hướng dẫn giải

M = (− 25) + (−2) − (−75) + (−8)

= [(− 25) − (−75)] + [(−2) + (−8)]

= − (25 + 75) + (− 10)

= (− 100) + (− 10)

= − (100 + 10) = −110.