Với giải sách bài tập Toán 6 Bài 1: Số nguyên âm sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 1: Số nguyên âm

Bài 1 trang 46 sách bài tập Toán lớp 6 Tập 1: Số nguyên nào thích hợp để mô tả mỗi tình huống sau:

a) Thưởng 10 điểm trong một cuộc thi đấu

b) Bớt 4 điểm vi phạm luật

c) Nhiệt độ ngăn đá tủ là 5 độ dưới 0 độ C

d) Rút 3000000 đồng từ thẻ ATM

e) Đỉnh núi Fansipan (Phan-xi-păng) cao 3143 so với mực nước biển

Lời giải:

a) Số nguyên biểu diễn cho tình huống thưởng 10 điểm trong một cuộc thi đấu: +10

b) Số nguyên biểu diễn cho tình huống bớt 4 điểm vi phạm luật: -4

c) Số nguyên biểu diễn cho tình huống nhiệt độ ngăn đá tủ là 5 độ dưới 0 độ C-5

d) Số nguyên biểu diễn cho tình huống rút 3000000 đồng từ thẻ ATM- 3 000 000

e) Số nguyên biểu diễn cho tình huống đỉnh núi Fansipan (Phan-xi-păng) cao 3143 so với mực nước biển: +3 143

Bài 2 trang 47 sách bài tập Toán lớp 6 Tập 1: Cho trục số

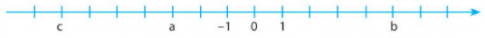
Hãy ghi số nguyên thích hợp vào vị trí trên trục số trong mỗi trường hợp sau:

a) Điểm nằm cách điểm a năm đơn vị về bên phải.

b) Điểm nằm cách điểm b bảy đơn vị về bên trái.

c) Điểm nằm cách điểm c mười đơn vị về bên phải.

d) Điểm nằm cách điểm a hai đơn vị về bên trái

Lời giải:

a) Từ điểm a trên trục số ta sẽ dịch chuyển sang bên phải 5 đơn vị ta được điểm 2:

b) Từ điểm b trên trục số ta sẽ dịch chuyển sang bên trái 7 đơn vị ta được điểm -2:

c) Từ điểm c trên trục số ta sẽ dịch chuyển sang bên phải 10 đơn vị ta được điểm 3:

d) Từ điểm a trên trục số ta sẽ dịch chuyển sang bên trái 2 đơn vị ta được điểm -5

Bài 3 trang 47 sách bài tập Toán lớp 6 Tập 1: Hãy vẽ một trục số, trên đó vẽ những điểm nằm cách điểm O năm đơn vị. Những điểm này biểu diễn các số nguyên nào?

Lời giải:

Ta có trục số sau: 

Điểm A và B là hai điểm nằm cách điểm O năm đơn vị

Điểm A biểu diễn số nguyên - 5 và điểm B biểu diễn số nguyên  5

Bài 4 trang 47 sách bài tập Toán lớp 6 Tập 1: Các phát biểu sau đúng hay sai?

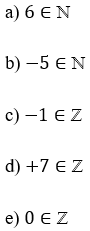
Lời giải:

Bài 5 trang 47 sách bài tập Toán lớp 6 Tập 1: Vẽ một đoạn của trục số từ -10 đến 10. Biểu diễn trên số đó các số nguyên sau đây:

Lời giải:

Ta có trục số sau:

Các điểm A, B, C, D, E, F, G, H, I, K lần lượt biểu diễn cho các số nguyên +4; -5; 0; -8; 2; -1; 7; 9; -9 trên trục số.

Bài 6 trang 47 sách bài tập Toán lớp 6 Tập 1: Tìm số đối của các số nguyên sau: -16; -10; 4; -4; 0; -100; 2021

Lời giải:

Số đối của -16 là: +16;

Số đối của -10 là: +10;

Số đối của 4 là: -4;

Số đối của -4 là: +4;

Số đối của 0 là: 0;

Số đối của -100 là: +100;

Số đối của 2 021 là: - 2 021.

Bài 7 trang 47 sách bài tập Toán lớp 6 Tập 1: Các điểm A, B, C, D trên trục số ở hình dưới đây biểu diễn các số nguyên nào?

Tìm số đối của các số nguyên đó

Lời giải:

Quan sát trục số, ta có:

Điểm A nằm cách điểm 0 năm đơn vị về bên trái nên điểm A biểu diễn số -5. Số đối của -5 là 5;

Điểm B nằm cách điểm 0 chín đơn vị về bên phải nên điểm B biểu diễn số 9. Số đối của 9 là -9;

Điểm C nằm cách điểm 0 ba đơn vị về bên phải nên điểm C biểu diễn số 3. Số đối của 3 là -3;

Điểm D nằm cách điểm 0 tám đơn vị về bên trái nên điểm D biểu diễn số -8. Số đối của -8 là 8.

Lý thuyết Số nguyên âm và tập hợp các số nguyên

1. Làm quen với số nguyên âm

Số nguyên âm được ghi như sau: −1; −2; −3; … và được đọc là: âm một, âm hai, âm ba, … hoặc trừ một, trừ hai, trừ ba, …

Ví dụ: Ta lấy vị trí tại mặt đất làm mốc. Đáy vịnh Cam Ranh thấp hơn mặt đất là 32 m. Tức là, độ cao của đáy vịnh Cam Ranh là – 32 m.

2. Tập hợp số nguyên

Các số tự nhiên khác 0 còn được gọi là các số nguyên dương.

− Số nguyên dương có thể được viết là: +1; +2; +3; … hoặc thông thường bỏ đi dấu “+” và chỉ ghi là: 1; 2; 3; …

Các số −1; −2; −3; … là các số nguyên âm.

Số 0 không phải là số nguyên âm và cũng không phải là số nguyên dương.

Tập hợp gồm các số nguyên âm, số 0 và các số nguyên dương được gọi là tập hợp số nguyên.

Ta kí hiệu tập hợp số nguyên là $\mathrm{\mathbb{Z}}$ . Như vậy, ta có: 

$\mathrm{\mathbb{Z}}$ = {…; −3; −2; −1; 0; 1; 2; 3; …}.

Ví dụ:

Số −12 là số nguyên âm, ta kí hiệu $-12\in \mathrm{\mathbb{Z}}$ .

Số 7 là số nguyên dương, ta kí hiệu $7\in \mathrm{\mathbb{Z}}$ .

Số 0 không phải là số nguyên âm và cũng không phải là số nguyên dương nhưng cũng là số nguyên, ta kí hiệu $0\in \mathrm{\mathbb{Z}}$ .

3. Biểu diễn số nguyên trên trục số

Người ta biểu diễn các số nguyên như trong hình dưới đây.

Hình biểu diễn các số nguyên như trên gọi là trục số.

Điểm 0 (không) được gọi là điểm gốc của trục số.

Chiều từ trái sang phải gọi là chiều dương, chiều từ phải sang trái gọi là chiều âm của trục số.

Điểm biểu diễn số nguyên a trên trục số gọi là điểm a.

Ví dụ: Hãy vẽ và biểu diễn các số −4; −2; 1; 3 trên trục số đó.

Hướng dẫn giải

Ta biểu diễn các số trên trục số như sau: 

− Biểu diễn số −4: Ta di chuyển 4 vạch về bên trái số 0.

− Biểu diễn số −2: Ta di chuyển 2 vạch về bên trái số 0.

− Biểu diễn số 1: Ta di chuyển 1 vạch về bên phải số 0. 

− Biểu diễn số 3: Ta di chuyển 3 vạch về bên phải số 0.

Khi đó, ta được trục số như sau: 

4. Số đối của một số nguyên

Hai số nguyên trên trục số nằm ở hai phía của điểm 0 và cách đều điểm 0 được gọi là hai số đối nhau.

Ví dụ: 4 là số đối của −4; −4 là số đối của 4.

9 là số đối của −9; −9 là số đối của 9.

Chú ý:

− Số đối của một số nguyên dương là một số nguyên âm.

− Số đối của một số nguyên âm là một số nguyên dương.

− Số đối của 0 là 0.