Với giải sách bài tập Toán 6 Bài 12: Ước chung. Ước chung lớn nhất sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 12: Ước chung. Ước chung lớn nhất

Bài 1 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm:

a) ƯC(24,36);

b) ƯC(60,140).

Lời giải:

a) Ta có: 24 = 2³.3;

36 = 2².3².

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2².3. 

⇒ƯCLN(24,36) = 12. 

Suy ra ƯC(24,36) = Ư(12) = {1; 2; 3; 4; 6; 12}.

Vậy ƯC(24,36) = {1; 2; 3; 4; 6; 12}.

b) Ta có: 60 = 2².3.5; 140 = 2².5.7.

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2².5 

⇒ƯCLN(60,140) = 20.

Suy ra ƯC(60,140) = Ư(20) = {1; 2; 4; 5; 10; 20}.

Vậy ƯC(60,140) = {1; 2; 4; 5; 10; 20}.

Bài 2 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm:

a) ƯCLN(3,24)

b) ƯCLN(8,1,32)

c) ƯCLN(36,72)

d) ƯCLN(24, 96, 120)

Lời giải:

a) Vì 24 = 8.3 nên 24 chia hết cho 3. Do đó ƯCLN(3,24) = 3.

b) ƯCLN(8,1,32) = 1.

c) Vì 72 = 36.2 nên 72 chia hết cho 36. Do đó ƯCLN(36,72) = 36.

d) Vì 96 = 24.4 nên 96 chia hết cho 24, 120 = 24.5 nên 120 cũng chia hết cho 24.

Do đó ƯCLN(24, 96, 120) = 24.

Bài 3 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm:

a) ƯCLN(56,140);

b) ƯCLN(90,135,270).

Lời giải:

a) Ta có: 56 = 2³.7, 140 = 2².5.7 

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2².7. 

⇒ƯCLN(56,140) = 2².7 = 28. 

Vậy ƯCLN(56,140) = 28

b) Ta có: 90 = 2.3².5, 135 = 3³.5, 270 = 2.3³.5

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2.3².5. 

⇒ƯCLN(90,135,270) = 3².5 = 9.5 = 45

Vậy ƯCLN(90,135,270) = 45.

Bài 4 trang 32 sách bài tập Toán lớp 6 Tập 1: Tìm ƯCLN rồi tìm các ước chung của:

a) 16 và 24;

b) 180 và 234;

c) 60, 90 và 135.

Lời giải:

a) Ta có: 16 = 2⁴, 24 = 2³.3

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2³.

⇒ƯCLN(16,24) = 2³ = 8.

⇒ƯC(16,24) = Ư(8) = {1; 2; 4; 8}.

Vậy ƯCLN(16,24) = 8 và ƯC(16,24) = {1; 2; 4; 8}.

b) Ta có: 180 = 2².3².5 và 234 = 2.3².13;

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 2.3².

⇒ƯCLN(180,234) = 2.3² = 2.9 = 18.

⇒ƯC(180,234) = Ư(18) = {1; 2; 3; 6; 9; 18}.

Vậy ƯCLN(180,234) = 18 và ƯC(180,234) = {1; 2; 3; 6; 9; 18}.

c) Ta có 60 = 2².3.5, 90 = 2.3².5 và 135 = 3³.5.

Lập tích các thừa số chung mỗi thừa số lấy số mũ nhỏ nhất, ta được: 3.5.

⇒ƯCLN(60,90,135) = 3.5 = 15.

⇒ƯC(60,90,135) = Ư(15) = {1; 3; 5; 15}.

Vậy ƯCLN(60,90,135) = 15 và ƯC(60,90,135) = {1; 3; 5; 15}..

Bài 5 trang 32 sách bài tập Toán lớp 6 Tập 1: Rút gọn các phân số sau để được phân số tối giản (có sử dụng ước chung lớn nhất):

Lời giải:

a) Ta có: 28 = 2².7, 36 = 2².3²

⇒ƯCLN(28,36) = 2² = 4.

Khi đó:

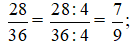
b) Ta có: 63 = 3².7, 90 = 2.3².5

⇒ƯCLN(63,90) = 3² = 9.

Khi đó:

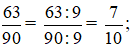
c) 40 = 2³.5, 120 = 2³.3.5.

⇒ƯCLN(40,120) = 2³.5 = 40.

Khi đó, ta có:

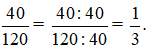
Bài 6 trang 32 sách bài tập Toán lớp 6 Tập 1: Hai phân số 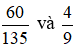 có bằng nhau không? Hãy giải thích. ....

Lời giải:

Ta thấy phân số 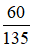 chưa tối giản nên ta sẽ rút gọn phân số này trước:

Ta có: 60 = 2²_.3.5, 135 = 3³.5

Suy ra ƯCLN(60, 135) = 3.5 = 15.

Khi đó: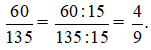 

Vậy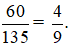 

Bài 7 trang 32 sách bài tập Toán lớp 6 Tập 1: Mai có một tờ giấy màu hình chữ nhật kích thước 20 cm và 30 cm. Mai muốn cắt tờ giấy thành các mảnh nhỏ hình vuông bằng nhau để làm thủ công sao cho tờ giấy được cắt vừa hết, không còn thừa mảnh nào. Tính độ dài lớn nhất của cạnh hình vuông nhỏ (số đo cạnh của hình vuông là một số tự nhiên với đơn vị là xăng-ti-mét).

Lời giải:

Do hình chữ nhật được cắt đều thành các hình vuông nhỏ nên độ dài cạnh hình vuông vuông nhỏ là ước chung của 20 và 30.

Suy ra độ dài lớn nhất của cạnh hình vuông nhỏ chính là ước chung lớn nhất của 20 và 30.

Ta có: 20 = 2².5, 30 = 2.3.5

⇒ ƯCLN(20, 30) = 2.5 = 10.

Vậy độ dài lớn nhất của cạnh hình vuông nhỏ là 10 cm.

Bài 8 trang 32 sách bài tập Toán lớp 6 Tập 1: Lớp bạn Hoa cần chia 171 chiếc bút bi, 63 chiếc bút chì và 27 cục tẩy vào trong các túi quà mang tặng các bạn ở trung tâm trẻ mồ côi sao cho số bút bi, bút chì và cục tẩy ở mỗi túi đều như nhau. Tính số lượng túi quà nhiều nhất mà các bạn lớp Hoa có thể chia. Khi đó, số lượng của mỗi loại bút bi, bút chì, cục tẩy trong mỗi túi là bao nhiêu?

Lời giải:

Do 171 chiếc bút bi, 63 chiếc bút chì và 27 cục tẩy được chia đều vào cùng một số lượng túi, nên số túi là ước chung của ba số 171, 63 và 27.

Số lượng túi quà nhiều nhất mà các bạn lớp Hoa có thể chia là ƯCLN(171,63,27).

Ta có: 171 = 3².19, 63 = 3².7, 27 = 3³.

Suy ra ƯCLN(171,63,27) = 3² = 9. 

Vậy số lượng túi quà nhiều nhất mà các bạn lớp Hoa có thể chia là 9 túi.

Khi đó, mỗi túi chứa:  Số bút bi là: 171 : 9 = 19 (chiếc)

Số bút chì là: 63 : 9 = 7 (chiếc)

Số cục tẩy là: 27 : 9 = 3 (cục)