Với giải sách bài tập Toán 6 Bài 5: Thứ tự thực hiện phép tính sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 5: Thứ tự thực hiện phép tính
Bài 1 trang 17 sách bài tập Toán lớp 6 Tập 1: Thực hiện phép tính:
a) {[(37 + 13) : 5] - 45 : 5}.7;
b) 62.10:{780:[103 – (2.53 + 35.14)]}.
Lời giải:
a) {[(37 + 13) : 5] - 45 : 5}.7;
={[50:5] − 45:5}.7
={10 − 45:5}.7
={10 − 9}.7
= 1.7
= 7.
b) 62.10:{780:[103 – (2.53 + 35.14)]}
= 36.10:{780:[1 000 – (2.125 + 35.14)]}
= 360:{780:[1 000 – (250 + 490)]}
= 360:{780:[1 000 – 740]}
= 360:{780:260}
= 360:{780:260}
= 360:3
= 120.
Bài 2 trang 17 sách bài tập Toán lớp 6 Tập 1: Tính nhanh: a) 432 + 43.57;
a) 432 + 43.57;
b) 592 – 59.19;
c) 119.34 + 81.
Lời giải:
a) 432 + 43.57
= 43.43 + 43.57
= 43.(43 + 57)
= 43.100
= 4 300.
b) 592 – 59.19
= 59.59 – 59.19
= 59.(59 – 19)
= 59.40
= 2 360.
c) 119.34 + 81
= 119.81 + 81.1
= 81.(119 + 1)
= 81.120
= 9 720.
Bài 3 trang 17 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên x, biết:
a) 24.(x – 16) = 122;
b) (x2 – 10):5 = 3.
Lời giải:
a) 24.(x – 16) = 122
24.(x – 16) = 144
x – 16 = 6
x = 16 + 6
x = 22.
Vậy x = 22.
b) (x2 – 10):5 = 3
x2 – 10 = 3.5
x2 – 10 = 15
x2 = 10 + 15
x2 = 25
x2 = 52
x = 5.
Vậy x = 5.
2021.2022.2023.2024 + 2025.2026.2027.2028.2029
Lời giải:
Xét tích 2021.2022.2023.2024 có chữ số tận cùng của tích 1.2.3.4 (= 24) là chữ số 4.
Xét tích 2025.2026.2027.2028.2029 là chữ số tận cùng của tích 5.6.7.8.9 (= 15120) là chữ số 0.
Vậy chữ số tận cùng của tổng cần tìm là chữ số 4.
Lý thuyết Thứ tự thực hiện các phép tính
1. Thứ tự thực hiện phép tính
Khi thực hiện các phép tính trong một biểu thức:
− Đối với biểu thức không có dấu ngoặc:
+ Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
− Đối với biểu thức có dấu ngoặc:
+ Nếu biểu thức có các dấu ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính trong dấu ngoặc tròn trước, rồi thực hiện phép tính trong dấu ngoặc vuông, cuối cùng thực hiện phép tính trong dấu ngoặc nhọn.
Ví dụ: Tính.
a) 32 . 14 – 51 . 6;
b) 12 . {423 + [28.15 – (8 + 18) + 125]}.
Hướng dẫn giải
a) 32 . 14 – 51 . 6
= 448 – 306
= 142.
b) 12 . {423 + [28 . 15 – (8 + 18) + 125]}
= 12 . {423 + [28 . 15 – 26 + 125]}
= 12 . {423 + [420 – 26 + 125]}
= 12 . {423 + [394 + 125]}
= 12 . {423 + 519}
= 12 . 942
= 11 304.
2. Sử dụng máy tính cầm tay
− Nút mở máy:
− Nút tắt máy:
− Các nút số từ 0 đến 9.
− Nút dấu cộng, dấu trừ, dấu nhân, dấu chia.
− Nút dấu “=” cho phép hiện ra kết quả trên màn hình số.
− Nút xóa (xóa số vừa đưa vào bị nhầm):
− Nút xóa toàn bộ phép tính (và kết quả) vừa thực hiện:
− Nút dấu ngoặc trái và phải:
− Nút tính lũy thừa:
Ví dụ: Sử dụng máy tính cầm tay, tính:
43 + (6 – 4) × 3.
Hướng dẫn giải
|
Biểu thức |
Nút ấn |
Kết quả |
Hiển thị trên màn hình |
|
43 + (6 – 4) × 3 |
 |
70 |
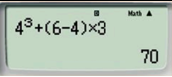 |
Vậy sử dụng máy tính cầm tay, ta tính được: 43 + (6 – 4) × 3 = 70.